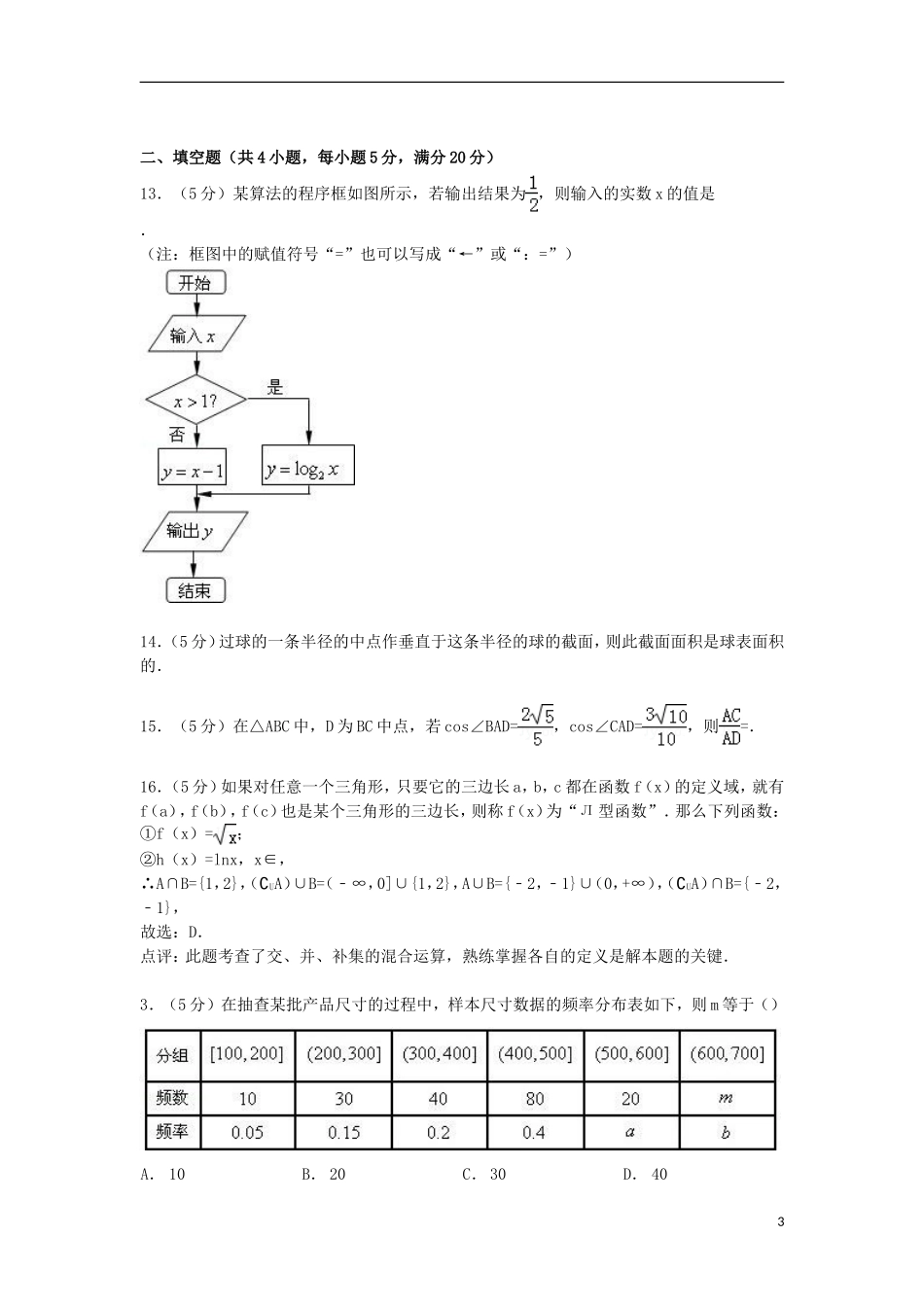
河南省中原名校2015届高三上学期第二次联考数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分,每小题只有一个选项符合题意)1.(5分)已知i是虚数单位,使(1+i)n为实数的最小正整数n为()A.2B.4C.6D.82.(5分)设U=R,集合A={y|y=,x>1},B={﹣2,﹣1,1,2},则下列结论正确的是()A.A∩B={﹣2,﹣1}B.(∁UA)∪B=(﹣∞,0)C.A∪B=(0,+∞)D.(∁UA)∩B={﹣2,﹣1}3.(5分)在抽查某批产品尺寸的过程中,样本尺寸数据的频率分布表如下,则m等于()A.10B.20C.30D.404.(5分)已知α,β是两个不同的平面,l,m,n是不同的直线,则正确命题为()A.若l⊥m,l⊥n,m⊂α,n⊂α,则l⊥αB.若l∥m,m⊂α,则l∥αC.若α⊥β,α∩β=l,m⊂α,m⊥l,则m⊥βD.若α⊥β,l⊥α,则l∥β5.(5分)已知双曲线﹣=1(a>0,b>0)的离心率为,则双曲线的渐近线方程为()A.y=±2xB.y=±xC.±xD.y=±x6.(5分)在△ABC中,点P在BC上,且,点Q是AC的中点,若,,则=()A.(﹣2,7)B.(﹣6,21)C.(2,﹣7)D.(6,﹣21)7.(5分)一个几何体的三视图如图所示,则该几何体的体积为()1A.B.C.D.8.(5分)下列说法中,不正确的是()A.“|x|=|y|”是“x=y”的必要不充分条件B.命题p:∀x∈R,sinx≤1,则¬p:∃x∈R,sinx>1C.“λ≤2”是“数列an=n2﹣λn+1(n∈N*)为递增数列”的充要条件D.命题p:所有有理数都是实数,q:正数的对数都是负数,则(¬p)∨(¬q)为真命题9.(5分)已知,则等于()A.B.C.D.10.(5分)设x,y满足约束条件,目标函数z=ax+by(a>0,b>0)的最大值为7,则+的最小值为()A.4B.C.D.711.(5分)(1+ax+by)n展开式中不含x的项的系数绝对值的和为243,不含y的项的系数绝对值的和为32,则a,b,n的值可能为()A.a=2,b=﹣1,n=5B.a=﹣2,b=﹣1,n=6C.a=﹣1,b=2,n=6D.a=1,b=2,n=512.(5分)已知函数f(x)=1+x﹣+﹣+…+,g(x)=1﹣x+﹣+…﹣,设F(x)=f(x+3)•g(x﹣4),且函数F(x)的零点均在区间(a<b,a,b∈Z)内,则b﹣a的最小值()A.8B.9C.10D.112二、填空题(共4小题,每小题5分,满分20分)13.(5分)某算法的程序框如图所示,若输出结果为,则输入的实数x的值是.(注:框图中的赋值符号“=”也可以写成“←”或“:=”)14.(5分)过球的一条半径的中点作垂直于这条半径的球的截面,则此截面面积是球表面积的.15.(5分)在△ABC中,D为BC中点,若cos∠BAD=,cos∠CAD=,则=.16.(5分)如果对任意一个三角形,只要它的三边长a,b,c都在函数f(x)的定义域,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“Л型函数”.那么下列函数:①f(x)=;②h(x)=lnx,x∈,∴A∩B={1,2},(∁UA)∪B=(﹣∞,0]∪{1,2},A∪B={﹣2,﹣1}∪(0,+∞),(∁UA)∩B={﹣2,﹣1},故选:D.点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.3.(5分)在抽查某批产品尺寸的过程中,样本尺寸数据的频率分布表如下,则m等于()A.10B.20C.30D.403考点:频率分布直方图.专题:计算题.分析:根据图中各组的频率之和等于1及频率的计算公式,结合题意可得a值,再由频率的计算公式可得其频率,进而可得答案.解答:解: 频率、频数的关系:频率=.∴∴a=0.1 根据表中各组的频率之和等于1得,∴b=1﹣0.9=0.1,∴m=20.故选B.点评:本题考查读频数分布表的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题,同时考查频率、频数的关系:频率=.4.(5分)已知α,β是两个不同的平面,l,m,n是不同的直线,则正确命题为()A.若l⊥m,l⊥n,m⊂α,n⊂α,则l⊥αB.若l∥m,m⊂α,则l∥αC.若α⊥β,α∩β=l,m⊂α,m⊥l,则m⊥βD.若α⊥β,l⊥α,则l∥β考点:空间中直线与直线之间的位置关系.专题:空间位置关系与距离.分析:由线面位置关系,逐个选项验证可得.解答:解:A选项,当l⊥m,l⊥n,m⊂α,n⊂...