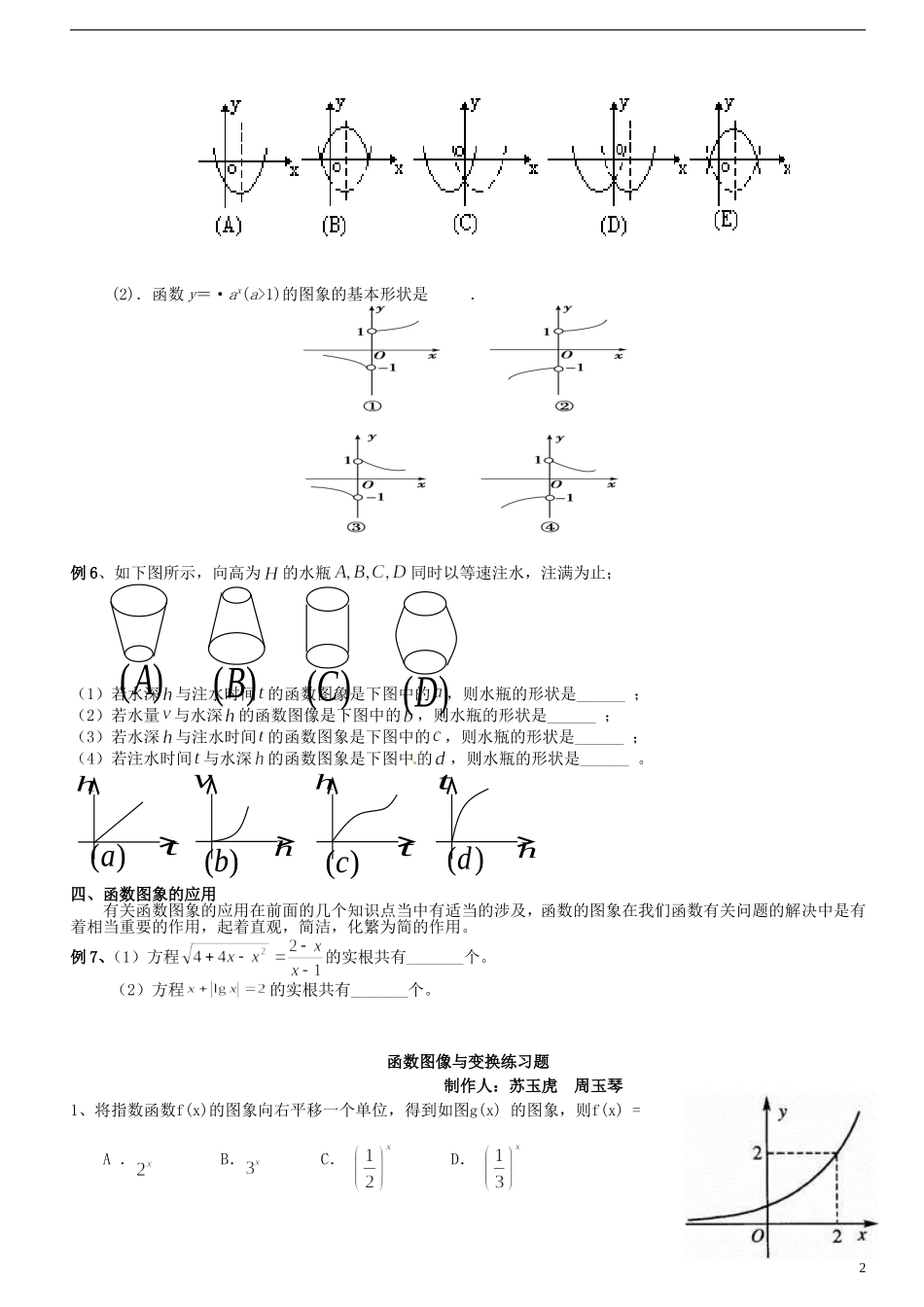
山西省朔州市平鲁区李林中学高三理科数学《编号19函数图像与变换》小练习一、图像变换函数的图象变换这一节的知识点是高考考查的重要方面,一些复杂的函数是可以通过一些较为简单的函数由相应的变换得到,从而我们可以利用之研究函数的性质。1.平移变换:(1)水平平移:函数的图像可以把函数的图像沿平移个单位即可得到;(2)竖直平移:函数的图像可以把函数的图像沿平移个单位即可得到.2.对称变换:(1)函数的图像可以将函数的图像关于即可得到;(2)函数的图像可以将函数的图像关于即可得到;(3)函数的图像可以将函数的图像关于即可得到;3.翻折变换:(1)函数的图像可以将函数的图像即可得到;(2)函数的图像可以将函数的图像即可得到.4.伸缩变换:(1)函数()的图像可以将函数的图像得到。(2)函数()的图像可以将函数的图像得到。例1、(1)设的图像与的图像关于直线对称,的图像由的图像右平移1个单位得到,则为__________(2)要得到的图像,只需作关于_____轴对称的图像,再向____平移3个单位而得到(3)将函数的图像上所有点的横坐标变为原来的(纵坐标不变),再将此图像沿轴方向向左平移2个单位,所得图像对应的函数为_____例2、已知f(x+199)=4x+4x+3(x∈R),那么函数f(x)的最小值为____.例3、若函数的图像经过第一、三、四象限,则一定有()A.B.C.D.二、函数图象的画法以解析式表示的函数作图象的方法有两种,即列表描点法和图象变换法,运用描点法作图象应避免描点前的盲目性,也应避免盲目地连点成线.要把表列在关键处,要把线连在恰当处.这就要求对所要画图象的存在范围、大致特征、变化趋势等作一个大概的研究.而这个研究要借助于函数性质、方程、不等式等理论和手段。用图象变换法作函数图象要确定以哪一种函数的图象为基础进行变换,以及确定怎样的变换。例4画出下列函数的图象(1)(2)(3)(4)三、函数图象的识别通过对函数解析式的形式了解函数的图象的特点,在识别上可以采用特殊的原则,去寻找特殊点和特殊位置等方法;在图象变换的问题上,需要依据变换的方法对函数的图象进行变换,而得到函数的图象。例5、(1)已知y=f(x)的图象如图(A),则y=f(-x)的图象是_______;y=-f(x)的图象是_______;y=f(x)的图象是______;y=f(x)的图象是_______。1(2).函数y=·ax(a>1)的图象的基本形状是_____.例6、如下图所示,向高为的水瓶同时以等速注水,注满为止;(1)若水深与注水时间的函数图象是下图中的,则水瓶的形状是______;(2)若水量与水深的函数图像是下图中的,则水瓶的形状是______;(3)若水深与注水时间的函数图象是下图中的,则水瓶的形状是______;(4)若注水时间与水深的函数图象是下图中的,则水瓶的形状是______。四、函数图象的应用有关函数图象的应用在前面的几个知识点当中有适当的涉及,函数的图象在我们函数有关问题的解决中是有着相当重要的作用,起着直观,简洁,化繁为简的作用。例7、(1)方程的实根共有_______个。(2)方程的实根共有_______个。函数图像与变换练习题制作人:苏玉虎周玉琴1、将指数函数f(x)的图象向右平移一个单位,得到如图g(x)的图象,则f(x)=A.B.C.D.()dth()bvh()cth()ath2()A()B()C()D2.函数y=-ex的图象()A.与y=ex的图象关于y轴对称B.与y=ex的图象关于坐标原点对称C.与y=e-x的图象关于y轴对称D.与y=e-x的图象关于坐标原点对称3.函数y=f(x)的图像与函数g(x)=log2x(x>0)的图像关于原点对称,则f(x)的表达式为()(A)f(x)=(x>0)(B)f(x)=log2(-x)(x<0)(C)f(x)=-log2x(x>0)(D)f(x)=-log2(-x)(x<0)4.函数的大致图象是()0000ABCD5.函数(且)的图象恒过一定点()A.(2,0)B.(0,2)C.(1,1)D.(1,0)6.函数的大致图象是()ABCD7、与函数的图像关于y轴对称的函数图像是8、函数y=1+ax(0