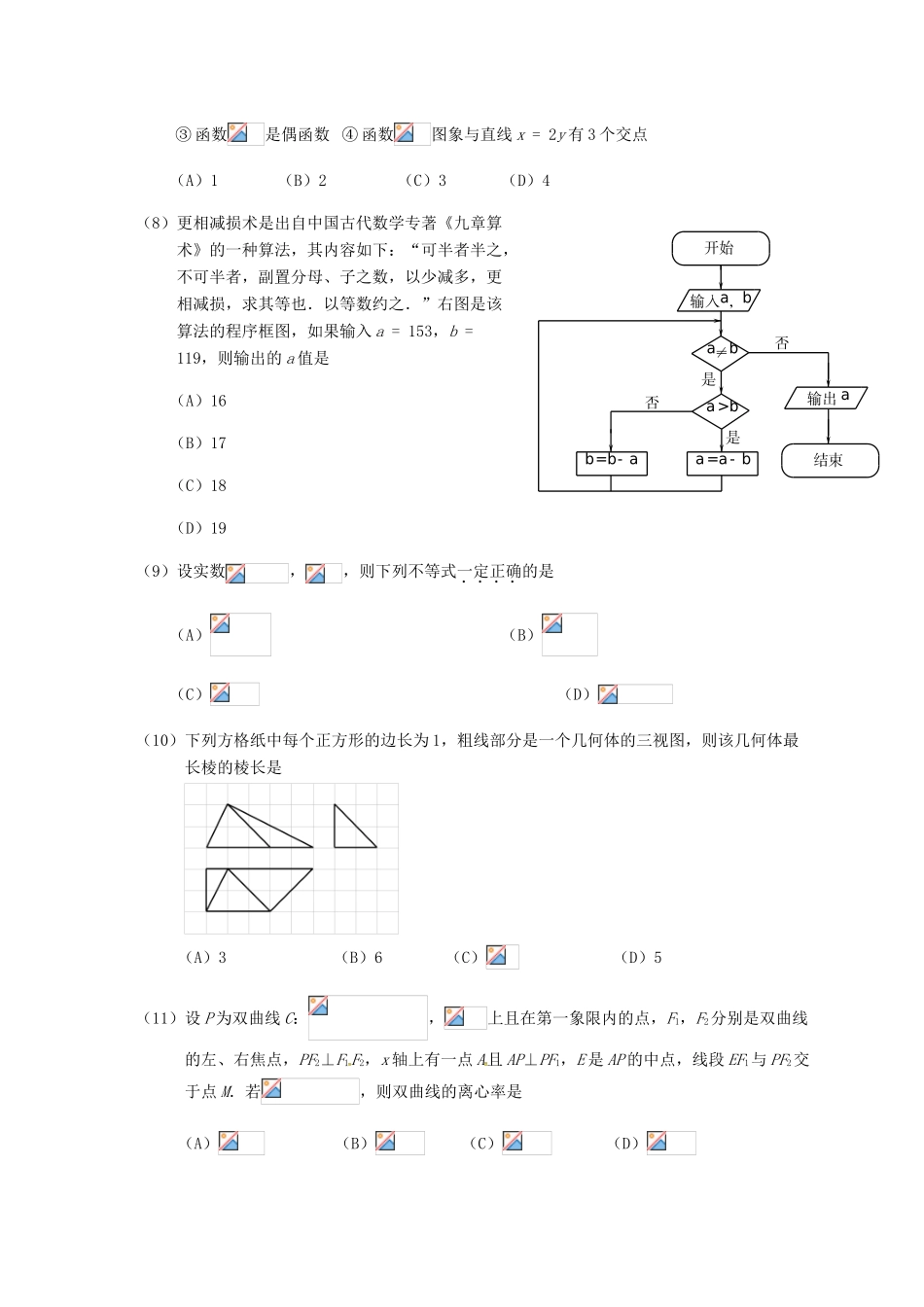
江西省南昌市十校2017届高三数学第二次模拟突破冲刺试题文(二)一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设集合,,则(A)(B)(C)(D)(2)设i为虚数单位,若是纯虚数,则a的值是(A)(B)0(C)1(D)2(3)若θ是第二象限角且sinθ=,则=(A)(B)(C)(D)(4)设F是抛物线E:的焦点,直线l过点F且与抛物线E交于A,B两点,若F是AB的中点且,则p的值是(A)2(B)4(C)6(D)8(5)为便民惠民,某通信运营商推出“优惠卡活动”.其内容如下:卡号的前7位是固定的,后四位从“0000”到“9999”共10000个号码参与该活动,凡卡号后四位带有“6”或“8”的一律作为优惠卡,则“优惠卡”的个数是(A)1980(B)4096(C)5904(D)8020(6)在△ABC中,点D是BC的中点,点E是AC的中点,点F在线段AD上并且AF=2DF,设=a,=b,则=(A)ab(B)ab(C)ab(D)ab(7)设表示m,n中最大值,则关于函数的命题中,真命题的个数是①函数的周期②函数的值域为③函数是偶函数④函数图象与直线x=2y有3个交点(A)1(B)2(C)3(D)4(8)更相减损术是出自中国古代数学专著《九章算术》的一种算法,其内容如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也.以等数约之.”右图是该算法的程序框图,如果输入a=153,b=119,则输出的a值是(A)16(B)17(C)18(D)19(9)设实数,,则下列不等式一定正确的是(A)(B)(C)(D)(10)下列方格纸中每个正方形的边长为1,粗线部分是一个几何体的三视图,则该几何体最长棱的棱长是(A)3(B)6(C)(D)5(11)设P为双曲线C:,上且在第一象限内的点,F1,F2分别是双曲线的左、右焦点,PF2⊥F1F2,x轴上有一点A且AP⊥PF1,E是AP的中点,线段EF1与PF2交于点M.若,则双曲线的离心率是(A)(B)(C)(D)否结束输出a否b=b-aa=a-b是是a>ba≠b输入a,b开始(12)设函数=x·ex,,,若对任意的,都有成立,则实数k的取值范围是(A)(B)(C)(D)第Ⅱ卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(23)题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分.(13)的展开式中,x5的系数是.(用数字填写答案)(14)若,,,且,那么与的夹角为.(15)已知四棱锥的外接球为球,底面是矩形,面底面,且,,则球的表面积为.(16)已知函数,当有最大值,且最大值大于时,则的取值范围是.三、解答题:解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分12分)已知中,角,,的对边分别为,,,已知向量,且.(Ⅰ)求角的大小;(Ⅱ)若的面积为,,求.(18)(本小题满分12分)如图的几何体中,平面,平面,为等边三角形,,为的中点.(Ⅰ)求证:平面;(Ⅱ)求到平面的距离.(19)(本小题满分12分)一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:x[11,13)[13,15)[15,17)[17,19)[19,21)[21,23)频数2123438104(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.(20)(本小题满分12分)已知椭圆C:的右焦点为F,右顶点为A,设离心率为e,且满足,其中O为坐标原点.(Ⅰ)求椭圆C的方程;(Ⅱ)过点的直线l与椭圆交于M,N两点,求△OMN面积的最大值.(21)(本小题满分12分)已知函数存在两个极值点.(Ⅰ)求实数a的取值范围;(Ⅱ)设和分别是的两个极值点且,证明:.请考生从(22)、(23)两题中任选一题作答.如果多做,则按所做第一个题目计分.(22)(本小题满分10分)选修4—4:坐标系与参数方程在平面直角坐标系xOy中,曲线C1的参数方程为(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:.(Ⅰ)求曲线C1和C2的直角坐标方程,并分别指出其曲线类型;(Ⅱ)试判断:曲线C1和C2是否有公共点?...