单元质量测试(五)时间:120分钟满分:150分第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.[2017·安徽安庆质检]设i是虚数单位,如果复数的实部与虚部相等,那么实数a的值为()A.B.-C.3D.-3答案C解析=,由题意知2a-1=a+2,解之得a=3.2.[2016·广东测试]若z=(a-)+ai为纯虚数,其中a∈R,则=()A.iB.1C.-iD.-1答案C解析 z为纯虚数,∴a=,∴====-i.3.设0
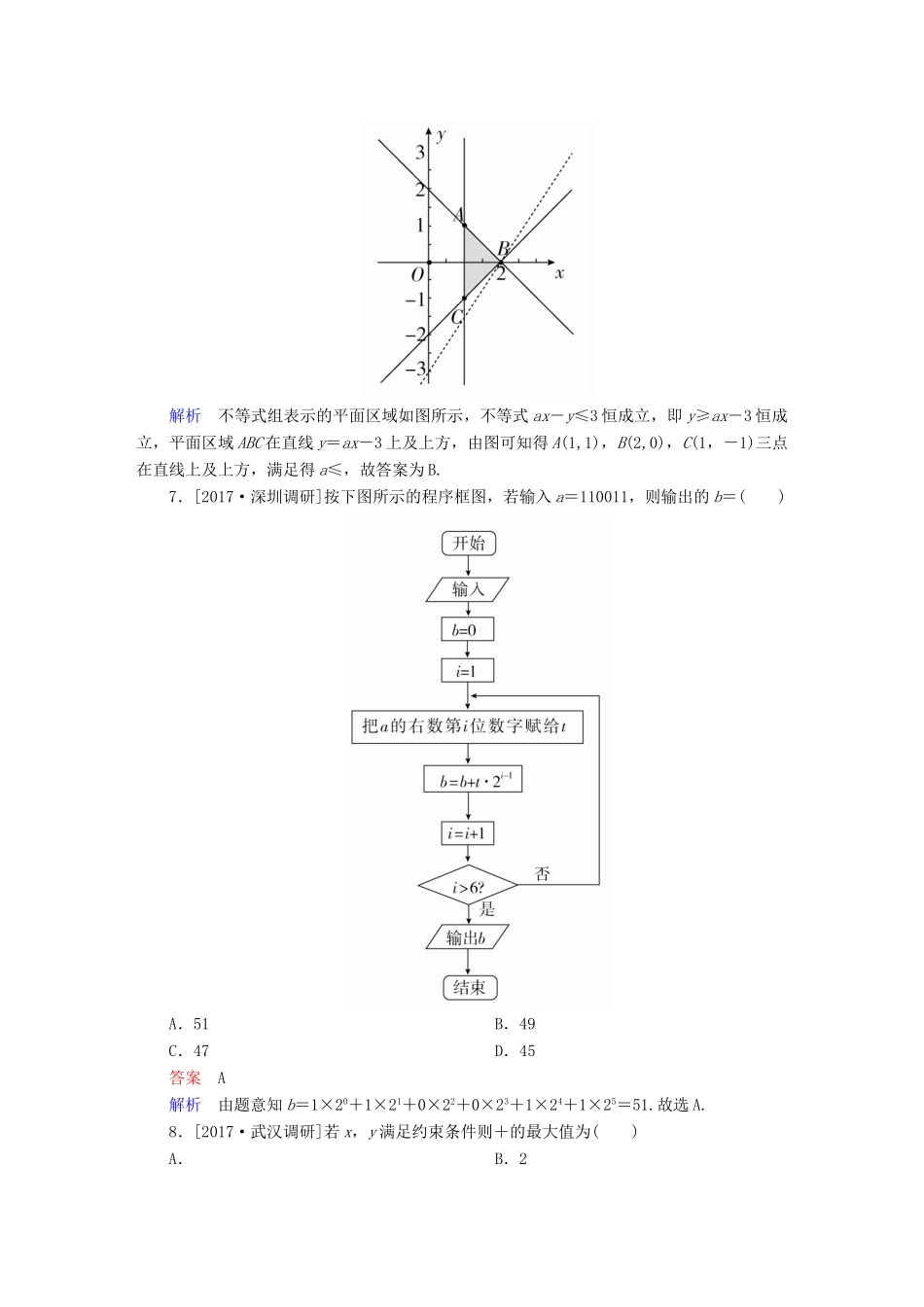
0时才能成立,所以p真q假.所以选C.5.不等式≤x-2的解集是()A.(-∞,0]∪(2,4]B.[0,2)∪[4,+∞)C.[2,4)D.(-∞,2]∪(4,+∞)答案B解析①当x-2>0,即x>2时,原不等式可化为(x-2)2≥4,∴x≥4;②当x-2<0,即x<2时,原不等式可化为(x-2)2≤4,∴0≤x<2.6.[2016·福建宁德调研]已知实数x,y满足若不等式ax-y≤3恒成立,则实数a的取值范围为()A.(-∞,4]B.C.D.[2,4]答案B解析不等式组表示的平面区域如图所示,不等式ax-y≤3恒成立,即y≥ax-3恒成立,平面区域ABC在直线y=ax-3上及上方,由图可知得A(1,1),B(2,0),C(1,-1)三点在直线上及上方,满足得a≤,故答案为B.7.[2017·深圳调研]按下图所示的程序框图,若输入a=110011,则输出的b=()A.51B.49C.47D.45答案A解析由题意知b=1×20+1×21+0×22+0×23+1×24+1×25=51.故选A.8.[2017·武汉调研]若x,y满足约束条件则+的最大值为()A.B.2C.D.3答案D解析要求+的最大值,只要使x,y同时取得最小值即可,作出约束条件表示的平面区域如图中阴影部分所示,由图知x,y在点B处同时取得最小值,由方程组得所以max=+=3,故选D.9.不等式x2+2x<+对任意a,b∈(0,+∞)恒成立,则实数x的取值范围是()A.(-2,0)B.(-∞,-2)∪(0,+∞)C.(-4,2)D.(-∞,-4)∪(2,+∞)答案C解析不等式x2+2x<+对任意a,b∈(0,+∞)恒成立,等价于x2+2x0,+=1,所以a+b=ab,所以+===4b+16a-20.又4b+16a=4(b+4a)=4(b+4a)=20+4≥20+4×2=36,当且仅当=且+=1,即a=,b=3时取等号.所以+≥36-20=16.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.[2016·云南名校联考]观察下列等式:13=12,13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第n个等式为________.答案13+23+33+43+...