613平方根VIP免费

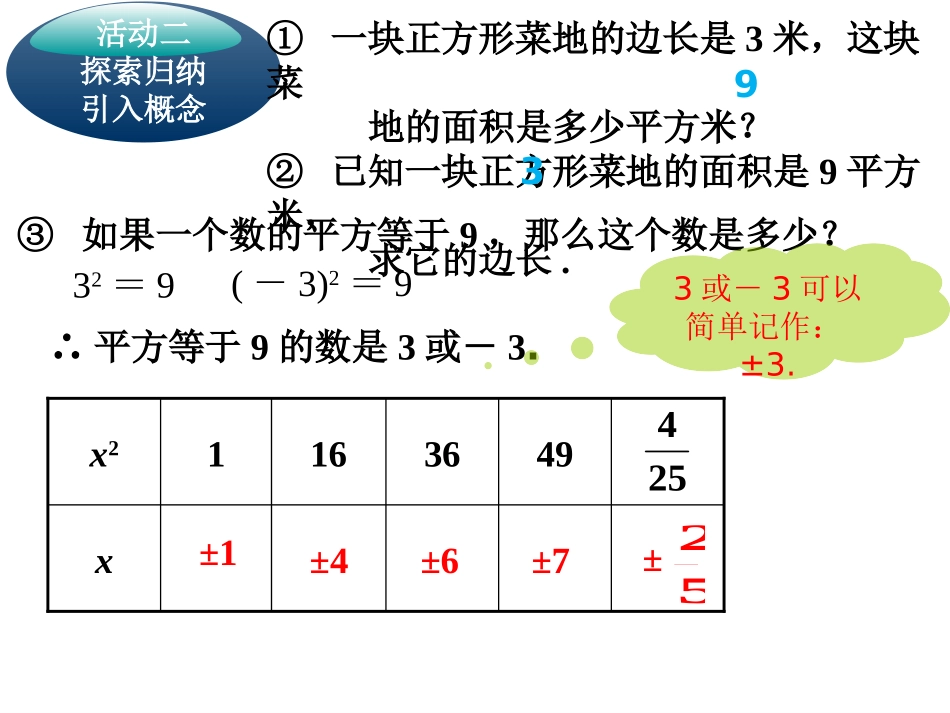
第六章实数6.1平方根活动一复习回顾引入新知什么是算术平方根?怎样表示?如果一个正数x的平方等于a，那么这个正数x叫做a的算术平方根.a的算术平方根表示为:0aa0的算术平方根是0负数没有算术平方根③如果一个数的平方等于9，那么这个数是多少？32＝9(－3)2＝9∴平方等于9的数是3或－3.3或－3可以简单记作：±3.x4936161x2254±1±4±6±752±活动二探索归纳引入概念①一块正方形菜地的边长是3米，这块菜地的面积是多少平方米？②已知一块正方形菜地的面积是9平方米，求它的边长.93活动二探索归纳引入概念一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根，这就是说，如果x2=a，那么x叫做a的平方根.平方根定义例如:3和-3是9的平方根，简记为±3是9的平方根.xx2求一个数a的平方根的运算，叫做开平方.平方与开平方互为逆运算！x2149+1-1+2-2+3-3149x+1-1+2-2+3-3平方开平方1.一个正数有几个平方根？它们有什么特点？2.0有几个平方根？是多少？3.负数有平方根吗？正数的平方根有两个，它们互为相反数.负数没有平方根.0有一个平方根，它是0本身.活动三探究性质深化概念平方根的性质读作“正、负根号a”25的平方根是±5，用符号语言表达为:正数a的算术平方根a正数a的算术平方根的相反数（即正数a的负的平方根）正数a的平方根表示a表示a表示例如：9的平方根是±3，用符号语言表达为:活动三探究性质深化概念25593平方根的表示方法例1.求下列各数的平方根.(1)100(2)(3)0.25169解：(1)(±10)∵2＝100，(3)(±0.5)∵2＝0.25，(2)(±)∵2＝，3416910010.∴100的平方根是±10；16934∴的平方根是±；93.164∴0.25的平方根是±0.5.0.250.5.例2.求下列各式的值.49(1)36(2)0.81(3)9解：(1)6∵2＝36，∴=6；36(2)∵0.92＝0.81，∴－＝－0.9；0.81(3)()∵2＝，∴±＝±.7373499499活动三探究性质深化概念36的算术平方根0.81的负的平方根的平方根499判断下列说法是否正确：（1）－9的平方根是－3；（）（2）49的平方根是7；（）（3）(－2)2的平方根是±2；（）（4）－1是1的平方根；（）××√√（5）的平方根是±4，16的算术平方根是4.（）16×1、下列等式正确的是()A.B.C.D.4164160.10.0122)(22、下列各式中没有平方根的是()A.B.C.D.21)(01001233、若一个数的平方根与它算术平方根的值相同，则这个数是()A．1B．0C．0或1D．1、0或-14、如果一个正数的平方根是a-1和a+3，则a=____，这个正数是＿＿.4-1CDB1、a的一个平方根是3，则另一个平方根是，a=.2、81的平方根是，的算术平方根是___.3、3a-2和2a-3是一个正数的两个平方根，则这两个平方根是和，这个数是.81-39拓展与应用（一）31-11±9