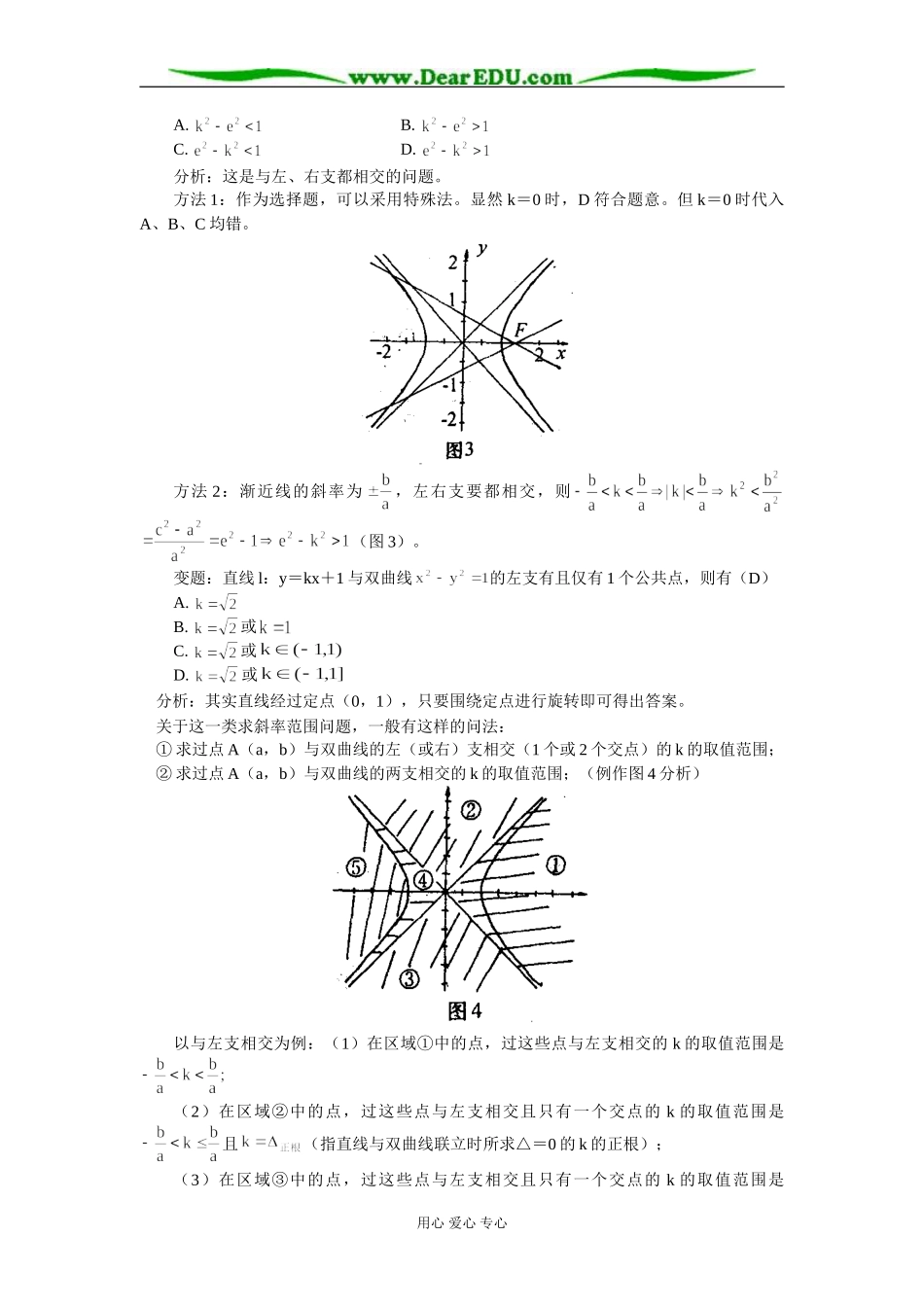
高中数学浅谈圆锥曲线中的数形结合思想学法指导杨海炎圆锥曲线中直线和圆锥曲线结合在一起的题目较多,下文主要阐述了用数形结合思想来解决两类问题。一、直线的条数我们在学习圆锥曲线的过程中,遇到了这样的问题:例1.过点A(0,2)可以作4条直线与双曲线有且只有一个公共点。这个结论可以引申:平面直角坐标系中任一点A(),过A与双曲线有且只有一个交点的直线条数问题。图示说明:(图1)可以证明:(1)区域①、②中的点,过这些点与双曲线有且只有一个交点的直线有4条。(2)在双曲线的两支上的点,过这些点与双曲线有且只有一个交点的直线有3条。(3)在双曲线的渐近线上的点(除原点)或在双曲线内部(区域③)的点,过这些点与双曲线有且只有一个交点的直线有2条。(4)过原点与双曲线有且只有一个交点的直线有0条。同样,我们也可以引申:平面直角坐标系中任一点A(),过A与抛物线有且只有一个交点的直线条数问题。图示说明:(图2)可以证明:(1)点在抛物线内部(区域①)时,过这些点与抛物线有且只有一个交点的直线有1条。(与对称轴平行的直线)(2)点在抛物线上时,过这些点与抛物线只有一个交点的直线有2条。(1条切线+1条与对称轴平行的直线)。(3)点在抛物线外(区域②)时,过这些点与抛物线只有一个交点的直线有3条。(2条切线+1条与对称轴平行的直线)。椭圆中,比较常规,这里从略。总结:要注意的是直线与圆锥曲线相交有且只有一个交点的情况未必相切,但相切必定只一个交点;掌握了这些区域的特点,关于这类直线条数的问题就迎刃而解了。二、直线的斜率关于直线与圆锥曲线相交、相切及直线条数的问题,我们还能引申到求直线的斜率问题,而这类问题又以双曲线比较典型,下面着重就双曲线中直线的斜率进行说明。例1.设离心率为e的双曲线C:的右焦点为F,直线l过点F且斜率k,直线l与双曲线C的左、右支都相交的充要条件是()。用心爱心专心A.B.C.D.分析:这是与左、右支都相交的问题。方法1:作为选择题,可以采用特殊法。显然k=0时,D符合题意。但k=0时代入A、B、C均错。方法2:渐近线的斜率为,左右支要都相交,则(图3)。变题:直线l:y=kx+1与双曲线的左支有且仅有1个公共点,则有(D)A.B.或C.或D.或分析:其实直线经过定点(0,1),只要围绕定点进行旋转即可得出答案。关于这一类求斜率范围问题,一般有这样的问法:①求过点A(a,b)与双曲线的左(或右)支相交(1个或2个交点)的k的取值范围;②求过点A(a,b)与双曲线的两支相交的k的取值范围;(例作图4分析)以与左支相交为例:(1)在区域①中的点,过这些点与左支相交的k的取值范围是(2)在区域②中的点,过这些点与左支相交且只有一个交点的k的取值范围是且(指直线与双曲线联立时所求△=0的k的正根);(3)在区域③中的点,过这些点与左支相交且只有一个交点的k的取值范围是用心爱心专心且(指直线与双曲线联立时所求△=0的k的负根);(4)在区域④中的点,过这些点与左支相交且只有一个交点的k的取值范围是且(指直线与双曲线联立时所求△=0的k的正、负根);(5)在区域⑤中的点,过这些点与左支相交且只有一个交点的k的取值范围是;说明:右支相交(1个或2个交点)、两支相交求对应的k的取值范围可以通过类似方法求之。圆锥曲线中有些问题直接用代数的方法来解决可能较为繁琐且不一定能得到正确答案,这时数形结合就是一种很好的思想,也是一种很好的解题策略。用心爱心专心