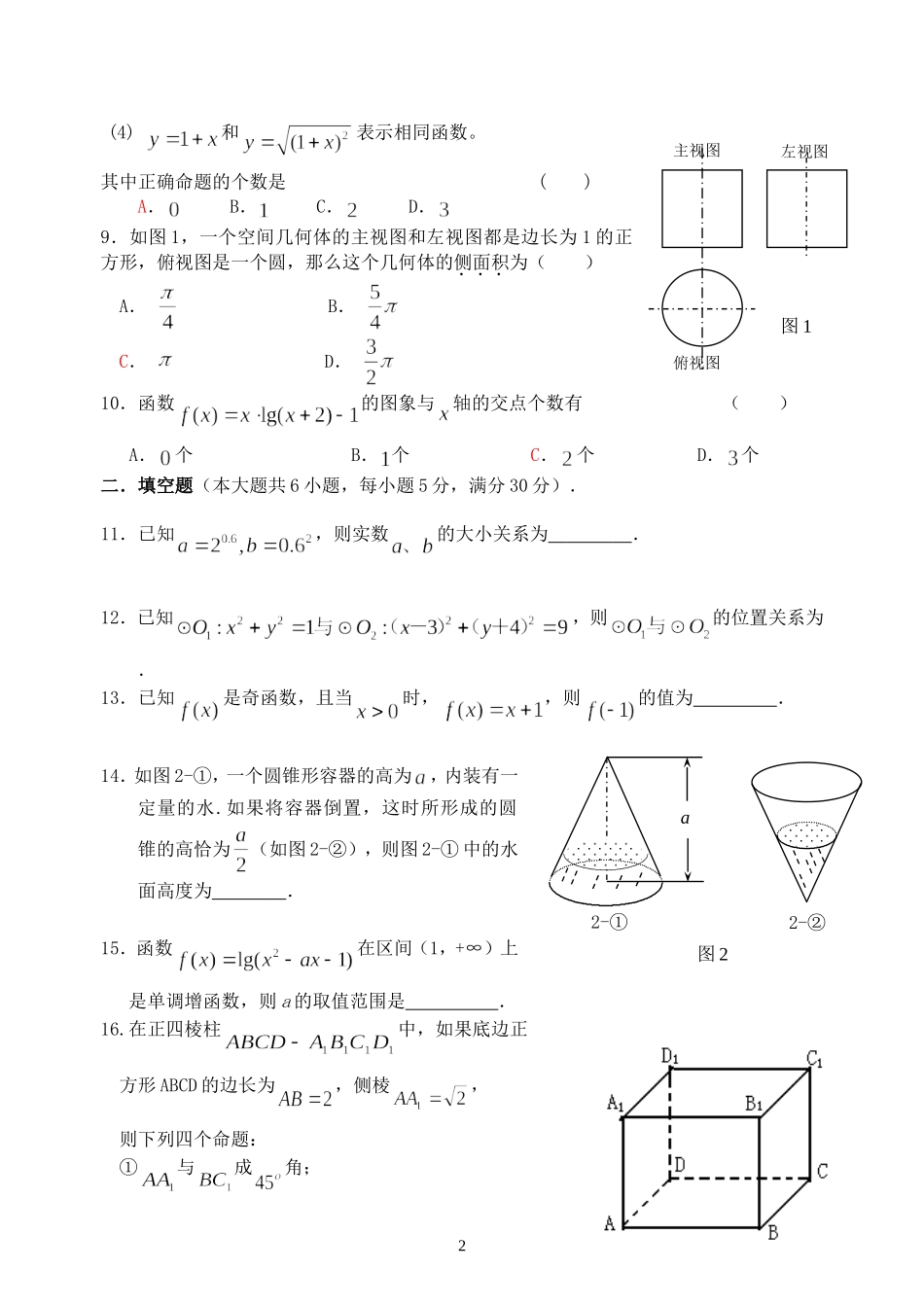
江苏省无锡市辅仁高中高一数学期初检测试卷2007-2一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.集合=()A.B.{1}C.{0,1,2}D.{-1,0,1,2}2.若,则等于()A.B.C.D.3.已知直线的方程为,则该直线的倾斜角为()A.B.C.D.4.已知两个球的表面积之比为1∶,则这两个球的半径之比为()A.1∶B.1∶C.1∶D.1∶5.下列函数中,在R上单调递增的是()A.B.C.D.6.已知点,且,则实数的值是()A.-3或4B.–6或2C.3或-4D.6或-27.已知直线、、与平面、,给出下列四个命题:①若m∥,n∥,则m∥n②若m⊥,m∥,则⊥③若m∥,n∥,则m∥n④若m⊥,⊥,则m∥或m其中假命题是()A.①B.②C.③D.④8.下列四个命题:(1)函数在时是增函数,也是增函数,所以是增函数;(2)若函数与轴没有交点,则和;(3)的递增区间只有;1(4)和表示相同函数。其中正确命题的个数是()A.B.C.D.9.如图1,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为()A.B.C.D.10.函数的图象与轴的交点个数有()A.个B.个C.个D.个二.填空题(本大题共6小题,每小题5分,满分30分).11.已知,则实数的大小关系为.12.已知,则的位置关系为.13.已知是奇函数,且当时,,则的值为.14.如图2-①,一个圆锥形容器的高为,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为(如图2-②),则图2-①中的水面高度为.15.函数在区间(1,+∞)上是单调增函数,则a的取值范围是.16.在正四棱柱中,如果底边正方形ABCD的边长为,侧棱,则下列四个命题:①与成角;2主视图左视图俯视图图1图22-①2-②a②与的距离为2;③二面角为;④平面.则正确命题的序号为.三.解答题(本大题共6小题,满分70分.解答应写出文字说明.证明过程或演算步骤).17.已知集合A=,B={x|2
1时满足A∩C≠φ-----------------------(12分)18.解:设直线为交轴于点,交轴于点,得,或解得或,或为所求。19.解:设这种放射性物质最初的质量是1,经过年后,剩留量是,则有.依题意,得,即.∴估计约经过4年,该物质的剩留量是原来的.20.解:设圆心为半径为,令而,或21.解:(Ⅰ),,又为正三5角形,E为AB的中点,而,又(Ⅱ)由(Ⅰ)得,AD在平面CDE上的射影为DE所以即为所成的角.为,且AE=2,AD=3,,即直线AD与平面CDE所成的角为(Ⅲ)取AB的中点M,连接DM,过C点在平面DCM内作于N证得,所以CM=,DM=,所以22.解:(1).---------------(1分)又--------------(2分).函数的定义域为集合D=.-----------(4分)(2)当有,=--(6分)同理,当时,有.任设,有为定义域上的奇函数.-----------(8分)(3)联立方程组可得,--------------------------(9分)(Ⅰ)当时,即时,方程只有唯一解,与题意不符;------(10分)(Ⅱ)当时,即方程为一个一元二次方程,要使方程有两个相异实数根,则解之得,但由于函数的图象在第二、四象限。-----------(13分)故直线的斜率综上可知或------------------(14分)6