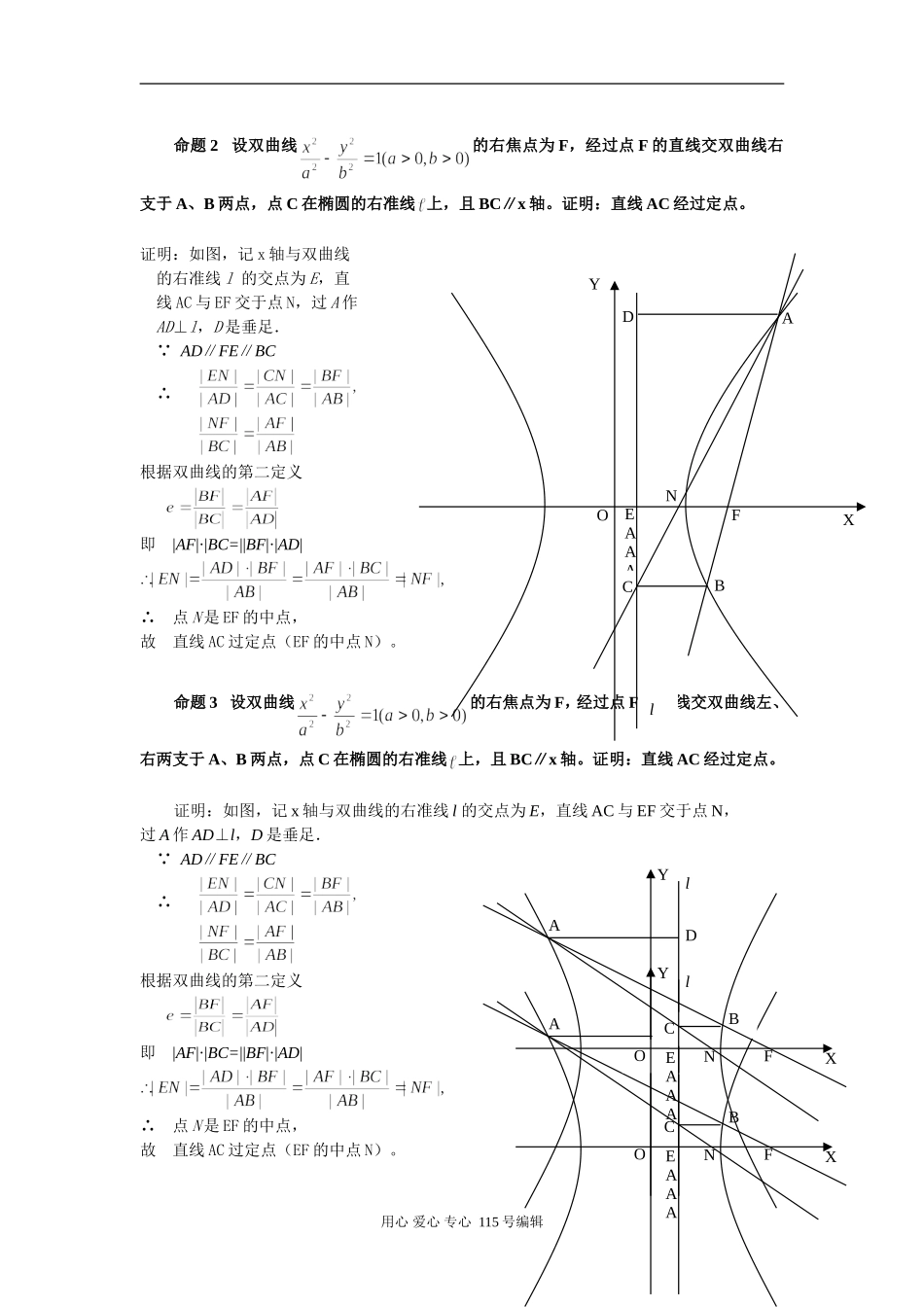
圆锥曲线的一个统一性质———由一道高考题引发出的思考衡阳县第三中学吴伟昌题(2001年全国·理):设抛物线y2=2px(p>0)的一个焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC∥x轴。证明:直线AC经过原点O。参考答案给出了如下的几何证法:证明:如图,记x轴与抛物线准线l的交点为E,过A作AD⊥l,D是垂足.则AD∥FE∥BC.连结AC,与EF相交手点N,则根据抛物线的几何性质,|AF|=|AD|,|BF|=|BC|即点N是EF的中点,与抛物线的顶点O重合,所以直线AC经过原点O.近几年,笔者在高三复习备考教学中,对该题的条件与结论进行一番探究,编拟如下一组命题,从而得到圆锥曲线的一个统一性质。命题1设椭圆的右焦点为F,经过点F的直线交椭圆于A、B两点,点C在椭圆的右准线上,且BC∥x轴。证明:直线AC经过定点。证明:如图,记x轴与椭圆的右准线l的交点为E,过A作AD⊥l,D是垂足.则AD∥FE∥BC.连结AC,与EF相交于点N,则根据椭圆的第二定义,即点N是EF的中点,∴直线AC经过EF的中点N。用心爱心专心115号编辑XEAAACONFYDBADlNEXCOFYBA命题2设双曲线的右焦点为F,经过点F的直线交双曲线右支于A、B两点,点C在椭圆的右准线上,且BC∥x轴。证明:直线AC经过定点。证明:如图,记x轴与双曲线的右准线l的交点为E,直线AC与EF交于点N,过A作AD⊥l,D是垂足.∵AD∥FE∥BC∴根据双曲线的第二定义即|AF|·|BC=||BF|·|AD|∴点N是EF的中点,故直线AC过定点(EF的中点N)。命题3设双曲线的右焦点为F,经过点F的直线交双曲线左、右两支于A、B两点,点C在椭圆的右准线上,且BC∥x轴。证明:直线AC经过定点。证明:如图,记x轴与双曲线的右准线l的交点为E,直线AC与EF交于点N,过A作AD⊥l,D是垂足.∵AD∥FE∥BC∴根据双曲线的第二定义即|AF|·|BC=||BF|·|AD|∴点N是EF的中点,故直线AC过定点(EF的中点N)。用心爱心专心115号编辑XEAAACONFDBAlYXEAAACONFDBAlYXEAAACONFDBAlY由此可见,这个直线过定点问题具有普遍性质,不是某一类圆锥曲线所特有的性质,而是圆锥曲线的一个统一性质。现将圆锥曲线这一个统一的性质归纳概括成如下定理:定理过圆锥曲线的焦点的直线交圆锥曲线于A、B两点,点C在相应的准线l上,且BC⊥l,则直线AC过定点。用心爱心专心115号编辑XEAAACONFDBAlY