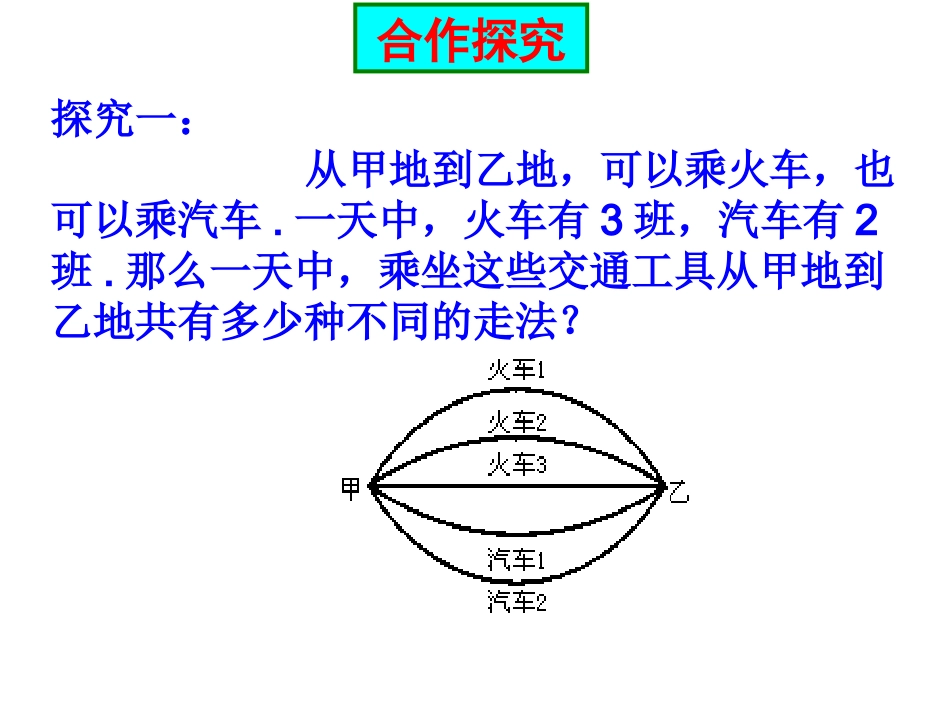
1.1分类计数原理与分步计数原理三都民族中学、高二数学备课组探究一:从甲地到乙地,可以乘火车,也可以乘汽车.一天中,火车有3班,汽车有2班.那么一天中,乘坐这些交通工具从甲地到乙地共有多少种不同的走法?合作探究完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法……在第n类办法中有mn种不同的方法.那么完成这件事共有N=m1+m2+…+mn种不同的方法.抽象概括分类计数原理:对于分类计数原理,注意以下几点:(1)从分类计数原理中可以看出,各类之间相互独立,都能完成这件事,且各类方法数相加,所以分类计数原理又称加法原理;(2)分类时,首先要根据问题的特点确定一个分类的标准,然后在确定的分类标准下进行分类;(3)完成这件事的任何一种方法必属于某一类,并且分别属于不同两类的两种方法都是不同的方法.深刻理解探究二:从甲地到乙地,要从甲地先乘火车到丙地,再于次日从丙地乘汽车到乙地.一天中,火车有3班,汽车有2班,那么两天中,从甲地到乙地共有多少种不同的走法?合作探究分步计数原理:完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法……做第n步有mn种不同的方法.那么完成这件事共有N=m1×m2×…×mn种不同的方法.抽象概括对于分步计数原理,应注意以下几点:(1)分步计数原理与“分步”有关,各个步骤相互依存,只有各个步骤完成了,这件事才算完成;分步计数原理又叫乘法原理。(2)分步时首先要根据问题的特点确定一个分步的标准;(3)分步时还要注意满足完成一件事必须并且只需连续完成n个步骤后这件事才算完成.深刻理解1.1.结合下列实例说明如何理解“完成一件事”:结合下列实例说明如何理解“完成一件事”:((11)从)从1010本不同的书中任取一本;本不同的书中任取一本;((22)从甲地经乙地到丙地;)从甲地经乙地到丙地;((33)从)从44名男运动员,名男运动员,33名女运动员中任选一人;名女运动员中任选一人;((44)从)从44名男运动员,名男运动员,33名女运动员中各选一人;名女运动员中各选一人;((55)袋中有)袋中有1010个不同编号的球,从中任意摸取两个球个不同编号的球,从中任意摸取两个球(每次摸一个);(每次摸一个);2.2.在完成上述事件时在完成上述事件时,,哪些与分类有关?哪些与分步有关?哪些与分类有关?哪些与分步有关?3.3.在计算完成事件的方法种数时在计算完成事件的方法种数时,,何时用加法原理何时用加法原理??何时用乘法原理?何时用乘法原理?4.4.这两个原理分别是怎样叙述的这两个原理分别是怎样叙述的??它们的根本区别是什么?它们的根本区别是什么?深刻理解例1.在1,2,3,…,200中,能够被5整除的数有多少个?解:能够被5整除的数,末位数字是0或者5,因此,我们把1,2,3….,200分成两类来计数:第一类:末位为0的有20个;第二类:末位为5的有20个.根据加法原理,在1,2,….,200中,能够被5整除的数有40个.练习:一同学有练习:一同学有44枚明朝不同古币和枚明朝不同古币和66枚清朝不同古枚清朝不同古币币..11)从中任取一枚,有多少种不同取法?)从中任取一枚,有多少种不同取法?22)从中任取明清古币各一枚,有多少种不同取法?)从中任取明清古币各一枚,有多少种不同取法?例题选讲例2.有一项活动,需在3名教师,8名男生和5名女生中选人参加.(1)若只需1人参加,有多少种选法?(2)若需教师,男生,女生各选一人参加,有多少种选法?解(1)只选1人就可以完成这件事而选出的1人有三种类型,即教师,男士,女生,因此要分类相加:第一类选出的是教师,有3种选法;第二类选出的是男生,有8种选法;第三类选出的是女生,有5种选法.根据加法原理,共有3+8+5=16种选法.(2)完成这件事需要分别选出1名教师,1名男生,1名女生,因此要分步完成:第一步:选1名教师,有3种选法;第二步:选1名男生,有8种选法;第三步:选1名女生,有5种选法;根据乘法原理共有120种选法.例题选讲例题讲解练习:练习:(1)(1)由数字由数字ll,,22,,33,,44,,55可以组成可以组成多少个数字不允许重复的三位数?多少个数字不允许重复的三位数?(2)(2)由数字由数字...