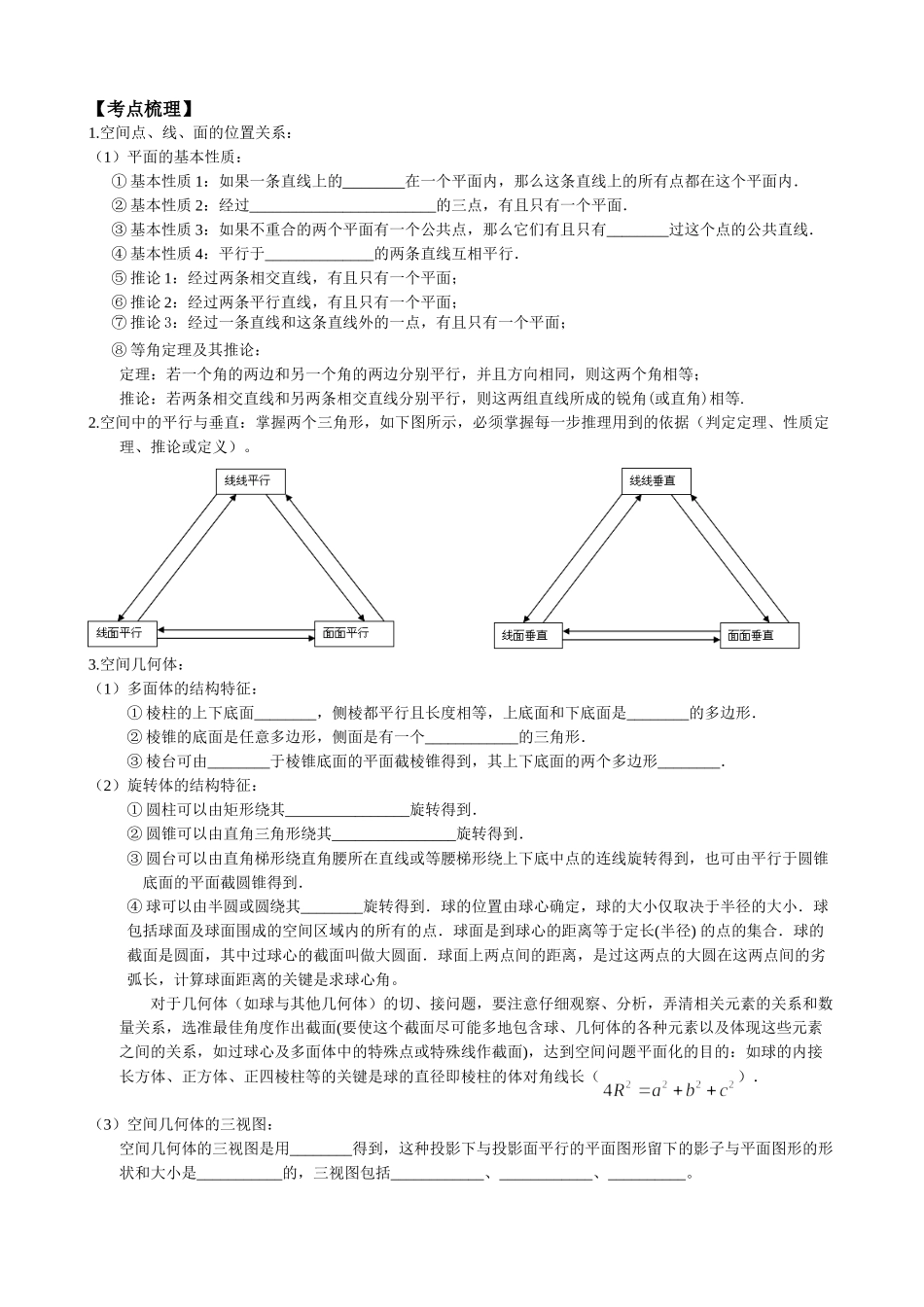
立体几何与空间向量【真题感悟】1.(2012安徽)设平面与平面相交于直线,直线在平面内,直线在平面内,且则“”是“”的充分不必要条件必要不充分条件充要条件即不充分不必要条件2.(2012北京)某三棱锥的三视图如图所示,该三梭锥的表面积是A.28+6B.30+6C.56+12D.60+123.(2012全国)已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=E为CC1的中点,则直线AC1与平面BED的距离为A2BCD14.(2012全国)三棱柱ABC-A1B1C1中,底面边长和侧棱长都相等,BAA1=CAA1=60°,则异面直线AB1与BC1所成角的余弦值为_________.5.(2011山东19)在如图所示的几何体中,四边形ABCD为平行四边形,090ACB,EA平面ABCD,//EFAB,//FGBC,//EGAC,2ABEF.(Ⅰ)若M是线段AD的中点,求证://GM平面ABFE;(Ⅱ)若2ACBCAE,求二面角ABFC的大小.ABCDEFGM【考点梳理】1.空间点、线、面的位置关系:(1)平面的基本性质:①基本性质1:如果一条直线上的________在一个平面内,那么这条直线上的所有点都在这个平面内.②基本性质2:经过________________________的三点,有且只有一个平面.③基本性质3:如果不重合的两个平面有一个公共点,那么它们有且只有________过这个点的公共直线.④基本性质4:平行于______________的两条直线互相平行.⑤推论1:经过两条相交直线,有且只有一个平面;⑥推论2:经过两条平行直线,有且只有一个平面;⑦推论3:经过一条直线和这条直线外的一点,有且只有一个平面;⑧等角定理及其推论:定理:若一个角的两边和另一个角的两边分别平行,并且方向相同,则这两个角相等;推论:若两条相交直线和另两条相交直线分别平行,则这两组直线所成的锐角(或直角)相等.2.空间中的平行与垂直:掌握两个三角形,如下图所示,必须掌握每一步推理用到的依据(判定定理、性质定理、推论或定义)。3.空间几何体:(1)多面体的结构特征:①棱柱的上下底面________,侧棱都平行且长度相等,上底面和下底面是________的多边形.②棱锥的底面是任意多边形,侧面是有一个____________的三角形.③棱台可由________于棱锥底面的平面截棱锥得到,其上下底面的两个多边形________.(2)旋转体的结构特征:①圆柱可以由矩形绕其________________旋转得到.②圆锥可以由直角三角形绕其________________旋转得到.③圆台可以由直角梯形绕直角腰所在直线或等腰梯形绕上下底中点的连线旋转得到,也可由平行于圆锥底面的平面截圆锥得到.④球可以由半圆或圆绕其________旋转得到.球的位置由球心确定,球的大小仅取决于半径的大小.球包括球面及球面围成的空间区域内的所有的点.球面是到球心的距离等于定长(半径)的点的集合.球的截面是圆面,其中过球心的截面叫做大圆面.球面上两点间的距离,是过这两点的大圆在这两点间的劣弧长,计算球面距离的关键是求球心角。对于几何体(如球与其他几何体)的切、接问题,要注意仔细观察、分析,弄清相关元素的关系和数量关系,选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系,如过球心及多面体中的特殊点或特殊线作截面),达到空间问题平面化的目的:如球的内接长方体、正方体、正四棱柱等的关键是球的直径即棱柱的体对角线长().(3)空间几何体的三视图:空间几何体的三视图是用________得到,这种投影下与投影面平行的平面图形留下的影子与平面图形的形状和大小是___________的,三视图包括____________、____________、__________。①在绘制三视图时,分界线和可见轮廓线都用实线画出,被遮挡的部分的轮廓线用虚线表示出来,即“眼见为实、不见为虚”.②空间几何体的数量关系也体现在三视图中,主视图和左视图的“高平齐”,主视图和俯视图的“长对正”,左视图和俯视图的“宽相等”.(4)空间几何体的直观图画空间几何体的直观图常用________画法,基本步骤是:①在已知图形中取互相垂直的x轴、y轴,两轴相交于点O,画直观图时,把它们画成对应的x′轴、y′轴,两轴相交于点O′,且使∠x′O′y′=45°(或135°).②已知图形中平行于x轴、y轴的线段,在直观图中分别平行于x′轴、y′轴....