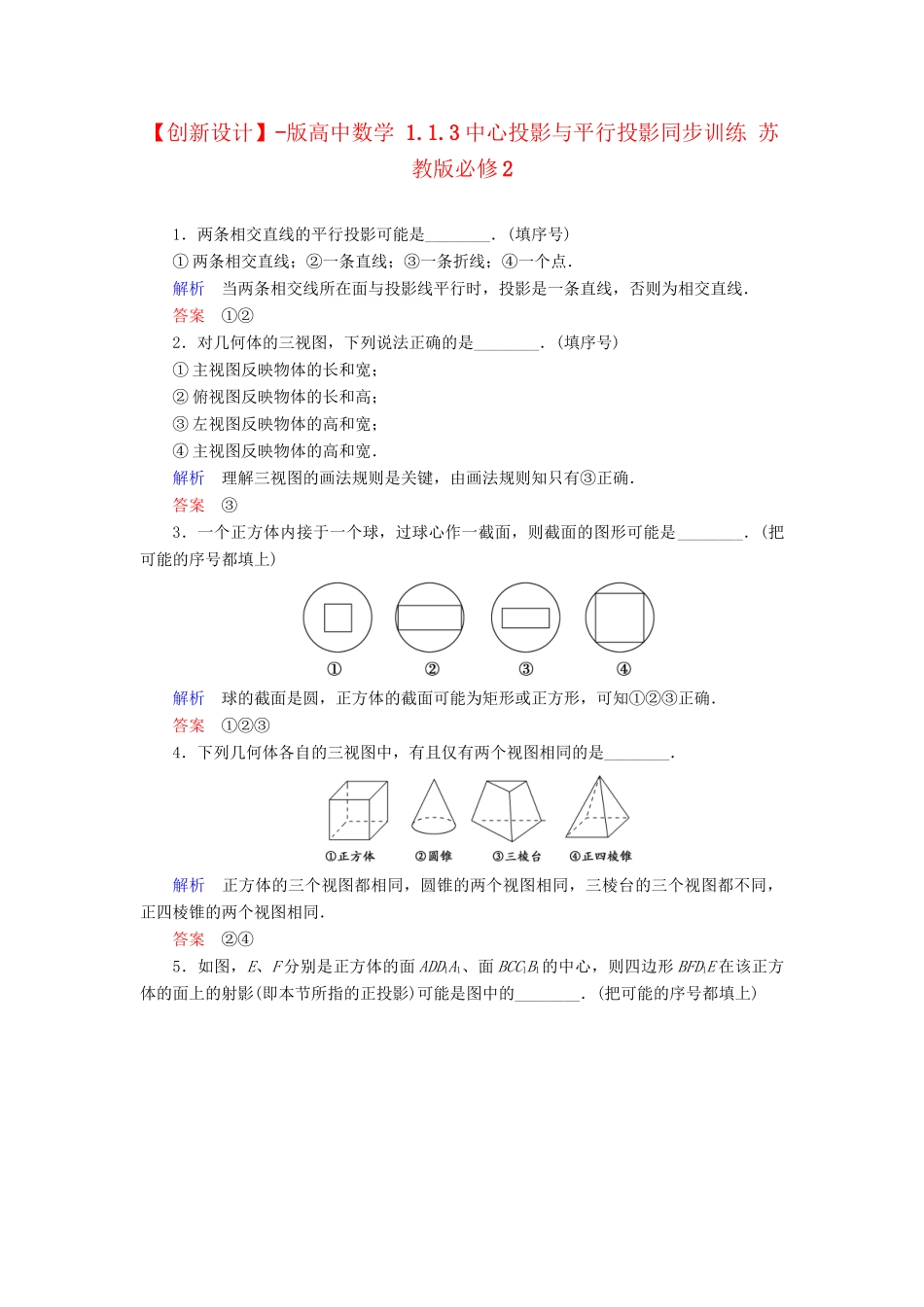
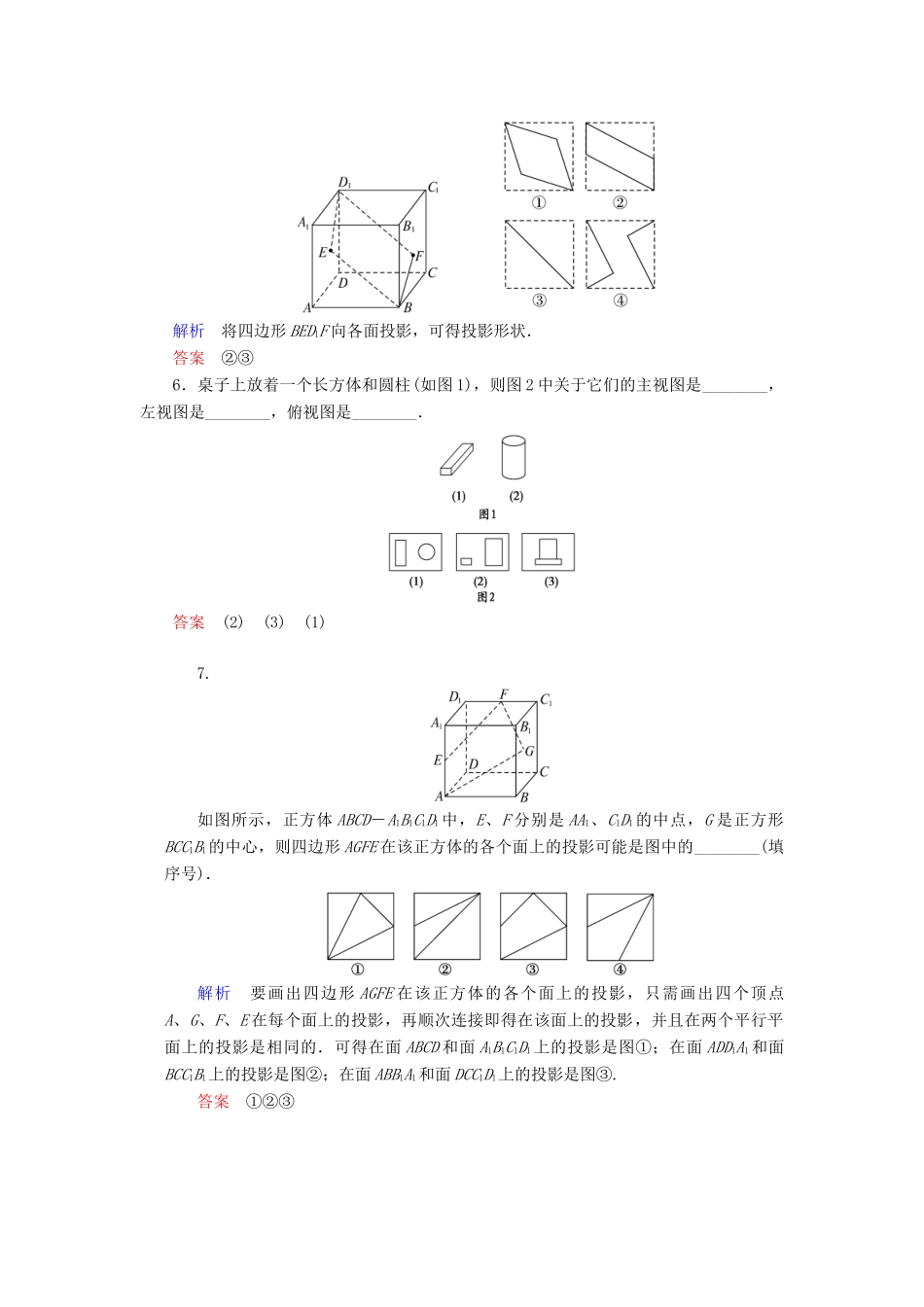
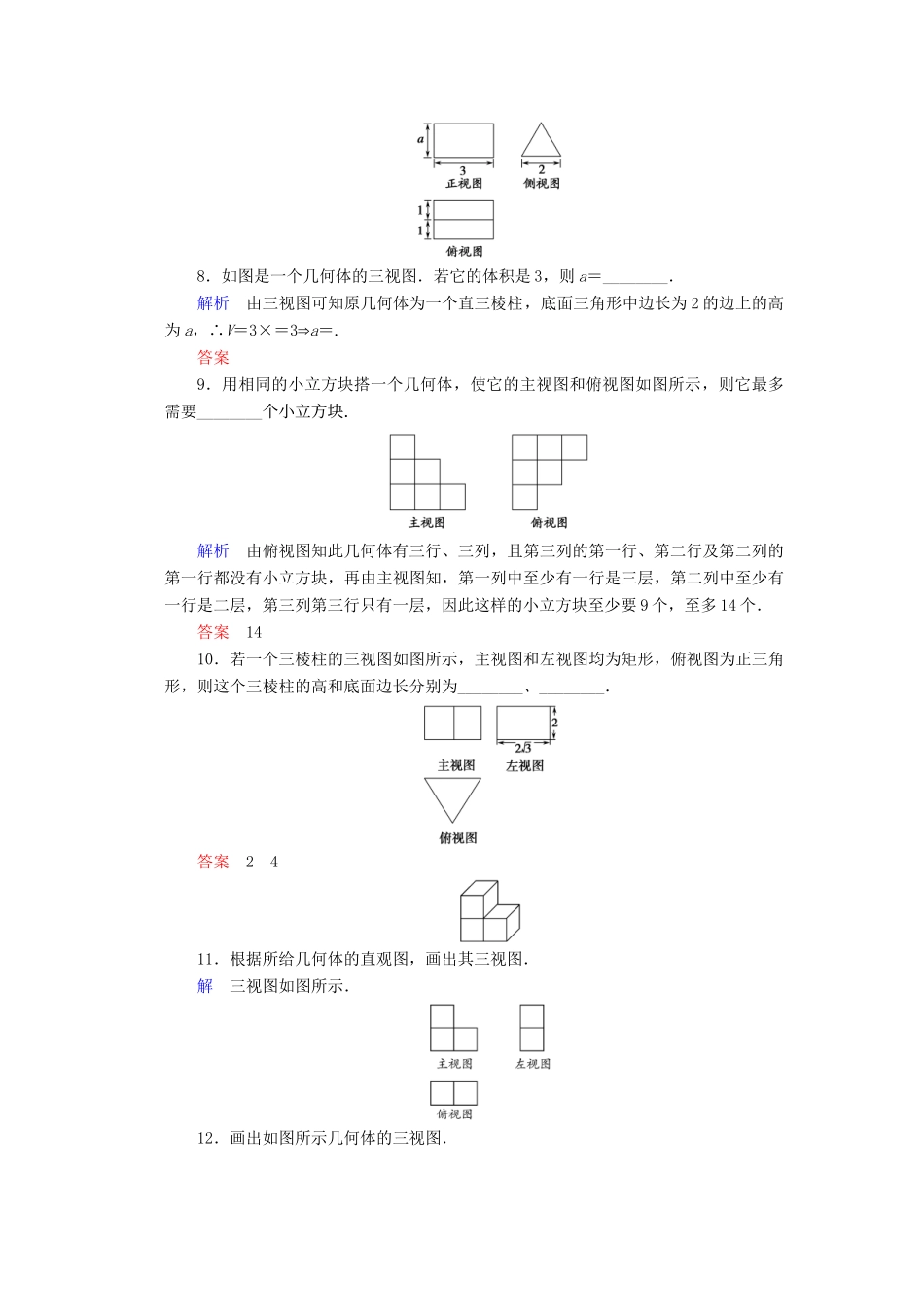
【创新设计】-版高中数学1.1.3中心投影与平行投影同步训练苏教版必修21.两条相交直线的平行投影可能是________.(填序号)①两条相交直线;②一条直线;③一条折线;④一个点.解析当两条相交线所在面与投影线平行时,投影是一条直线,否则为相交直线.答案①②2.对几何体的三视图,下列说法正确的是________.(填序号)①主视图反映物体的长和宽;②俯视图反映物体的长和高;③左视图反映物体的高和宽;④主视图反映物体的高和宽.解析理解三视图的画法规则是关键,由画法规则知只有③正确.答案③3.一个正方体内接于一个球,过球心作一截面,则截面的图形可能是________.(把可能的序号都填上)解析球的截面是圆,正方体的截面可能为矩形或正方形,可知①②③正确.答案①②③4.下列几何体各自的三视图中,有且仅有两个视图相同的是________.解析正方体的三个视图都相同,圆锥的两个视图相同,三棱台的三个视图都不同,正四棱锥的两个视图相同.答案②④5.如图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影(即本节所指的正投影)可能是图中的________.(把可能的序号都填上)解析将四边形BED1F向各面投影,可得投影形状.答案②③6.桌子上放着一个长方体和圆柱(如图1),则图2中关于它们的主视图是________,左视图是________,俯视图是________.答案(2)(3)(1)7.如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AA1、C1D1的中点,G是正方形BCC1B1的中心,则四边形AGFE在该正方体的各个面上的投影可能是图中的________(填序号).解析要画出四边形AGFE在该正方体的各个面上的投影,只需画出四个顶点A、G、F、E在每个面上的投影,再顺次连接即得在该面上的投影,并且在两个平行平面上的投影是相同的.可得在面ABCD和面A1B1C1D1上的投影是图①;在面ADD1A1和面BCC1B1上的投影是图②;在面ABB1A1和面DCC1D1上的投影是图③.答案①②③8.如图是一个几何体的三视图.若它的体积是3,则a=________.解析由三视图可知原几何体为一个直三棱柱,底面三角形中边长为2的边上的高为a,∴V=3×=3⇒a=.答案9.用相同的小立方块搭一个几何体,使它的主视图和俯视图如图所示,则它最多需要________个小立方块.解析由俯视图知此几何体有三行、三列,且第三列的第一行、第二行及第二列的第一行都没有小立方块,再由主视图知,第一列中至少有一行是三层,第二列中至少有一行是二层,第三列第三行只有一层,因此这样的小立方块至少要9个,至多14个.答案1410.若一个三棱柱的三视图如图所示,主视图和左视图均为矩形,俯视图为正三角形,则这个三棱柱的高和底面边长分别为________、________.答案2411.根据所给几何体的直观图,画出其三视图.解三视图如图所示.12.画出如图所示几何体的三视图.解几何体的三视图如下图所示.13.(创新拓展)如图,它是长方体截去一个角后的几何体,画出它的三视图.解析由三视图的画法,画好轮廓线.根据长方体的轮廓线和各面交线画三视图.答案长方体截角后,截面是一个三角形,在每个视图中反映为不同的三角形,三视图如图所示.