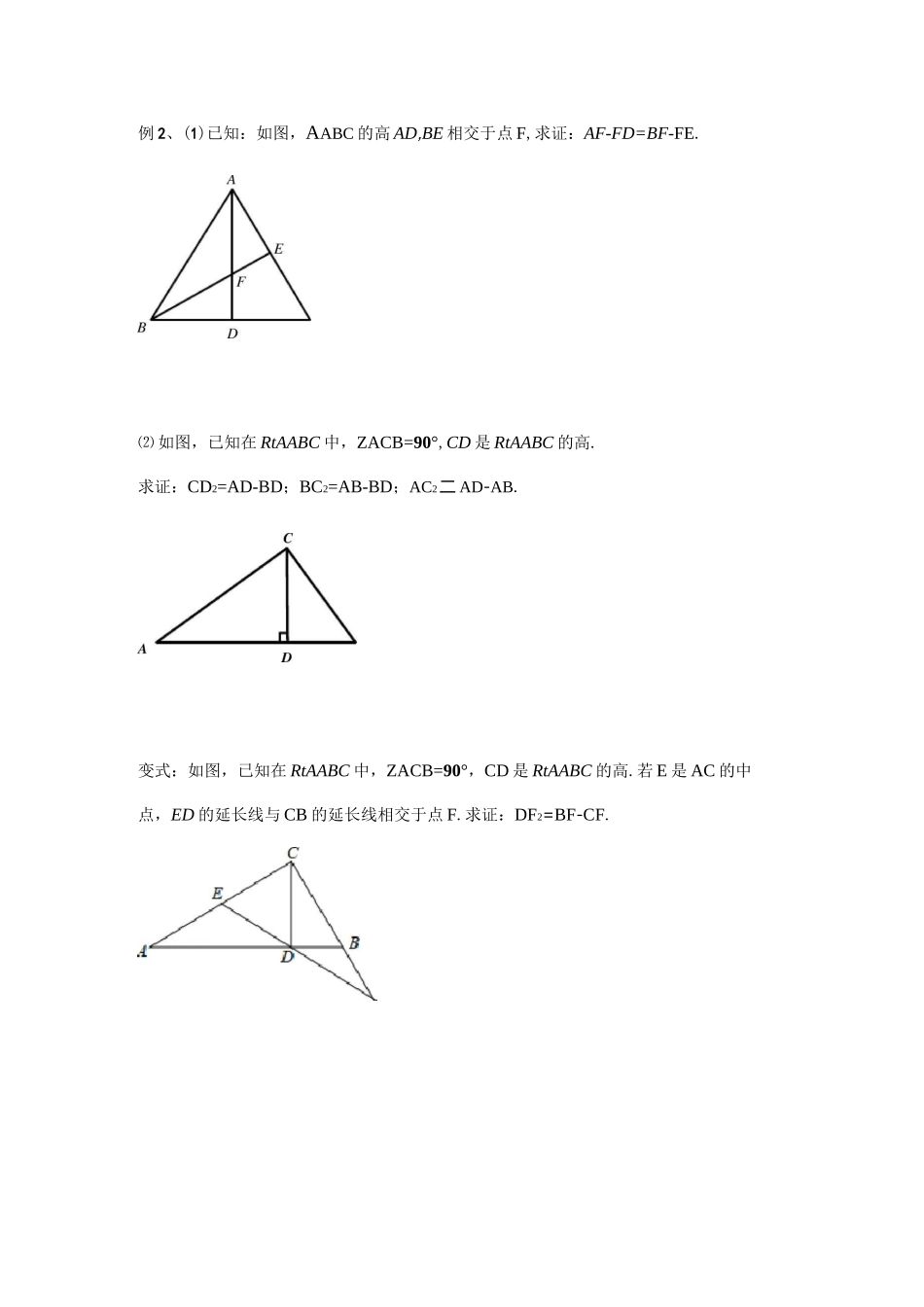
相似三角形及其判定一、知识导航1、相似三角形定义2、相似三角形判定二、典例精讲:精讲一、相似三角形定义:定义:对应角相等、对应边成比例的三角形,叫做相似三角形.相似用符号“S”表示,读作“相似于”,相似三角形对应边的比值叫做相似比(或相似系数).①记两个三角形相似时,和记两个三角形全等一样,通常把表示对应顶点的字母写在对应的位置上②全等是特殊的相似,相似比是1:1.全等要求形状相同与大小相等,而相似只是形状相同③由相似的定义,得相似三角形对应角相等,对应边成比例.④相似三角形有传递性:若AABCsAABC,AABCsAABC,则AABCAABC111222222333111333精讲二、相似三角形的判定:1、预备定理:平行于三角形一边的直线与另外两边(或两边的延长线)相交,所构成的三角形与原三角形相似.2、相似三角形的判定定理★判定定理1、如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应相等,两三角形相似.例1、(1)如图,B,C,D三点共线,且AB丄BD,DE丄BD,AC丄CE.求证:AABCsACDE.(2)如图B,C,D三点共线,且ZB=ZD=ZACE,求证:AABCsACDE.变式:1、如图,AABC中,ZACB=60。,点P是AABC内一点,使得ZAPB=ZBPC=ZCPA,求证:AAPCsACPB.2、已知APQR是等边三角形,ZAPB=120。,指出图中的相似三角形并证明.D例2、(1)已知:如图,AABC的高AD,BE相交于点F,求证:AF-FD=BF-FE.⑵如图,已知在RtAABC中,ZACB=90°,CD是RtAABC的高.求证:CD2=AD-BD;BC2=AB-BD;AC2二AD-AB.变式:如图,已知在RtAABC中,ZACB=90°,CD是RtAABC的高.若E是AC的中点,ED的延长线与CB的延长线相交于点F.求证:DF2=BF-CF.★判定定理2、如果一个三角形的两边与另一个三角形的两边对应成比例,且夹角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似.例3、(1)如图,已知AD-AB二AE-AC.贝y:①AADEsAACB;②AAEBsAADC正确的是;相似依据是.(2)如图,四边形ABEG、GEFH、HFCD都是边长为2的正方形.①求证:AAEFsACEA;②求ZAFB+ZACB的值.(3)如图,AABC是等边三角形,D为CB延长线上一点,E为BC延长线上点.①当BD、BC和CE满足什么条件时,AADBsAEAC?②当AADBsAEAC时,求ZDAE的度数.A变式:1、如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①②③④四个三角形.OA-OC二OB-OD,则①②③④哪些对应相似,请写出.2、如图,已知ZBAE=ZCAD,AB=18,AC=48,AE=15,AD=40.3、如图,在AABC和AADB中,ZABC=ZADB=90。,AC=5,AB=4,当BD的长是多少时,图中的两个直角三角形相似?例4、(1)如图,已知D为AABC内一点,E为AABC外一点,且Z1=Z2,Z3=Z4,求证:AABCsADBE.(2)如图,在AABC中,点D在边BC上,联结AD,ZADB=ZCDE,DE交边AC于点E,DE交BA延长线于点F,且AD2=DE-DF.求证:ABFDsACAD;变式:1、如图,BD,CE是AABC的高,求证:ZAED=ZACB.2、如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD-AE=AC-AG.求证:AD2=GD-DE.★判定定理3、如果一个三角形的三条边与另一个三角形的三边对应成比例,那么这两个三角形相似.简述为:三边对应成比例,两三角形相似.(3)已知RtAABC中,ZACB=90°,点D在BC边上,取AD、AB的中点E、F,连接CE、CF、EF,求证:ACEFsAADB.变式:如图,正方形ABCD中,E为AB中点,BC=4BF,那么图中与AADE相似的三角B.ABD.ABEF,AEDF例5、(1)如图,在正方形网格上的三角形①,②,③中,与AABC相似的三角形ABADsACAE.A.ACDF1、如图所示,给出下列条件:①ZB=ZACD②ZADC二ZACB;③ACAB~B自我测评④AC2二AD-AB.其中单独能够判定AABC-△ACD的是.(填番号)2、如图,AD是RtAABC斜边BC上的高,DE丄DF,且DE和DF分别交AB、AC于E、F.则AF-BD二AD-BE吗?说说你的理由.3、如图,在AABC中,点D在边AC上,AE分别交线段BD、边BC于点F、G,Z1=Z2,AF-BF二DF-EF,求证:BF2二FG-EF.4、已知:如图,竺=匹=兰,求证:AB=AE.ACABBCEC