高中数学 导数的应用 极值与最值课后练习一 新人教版选修2-2VIP免费

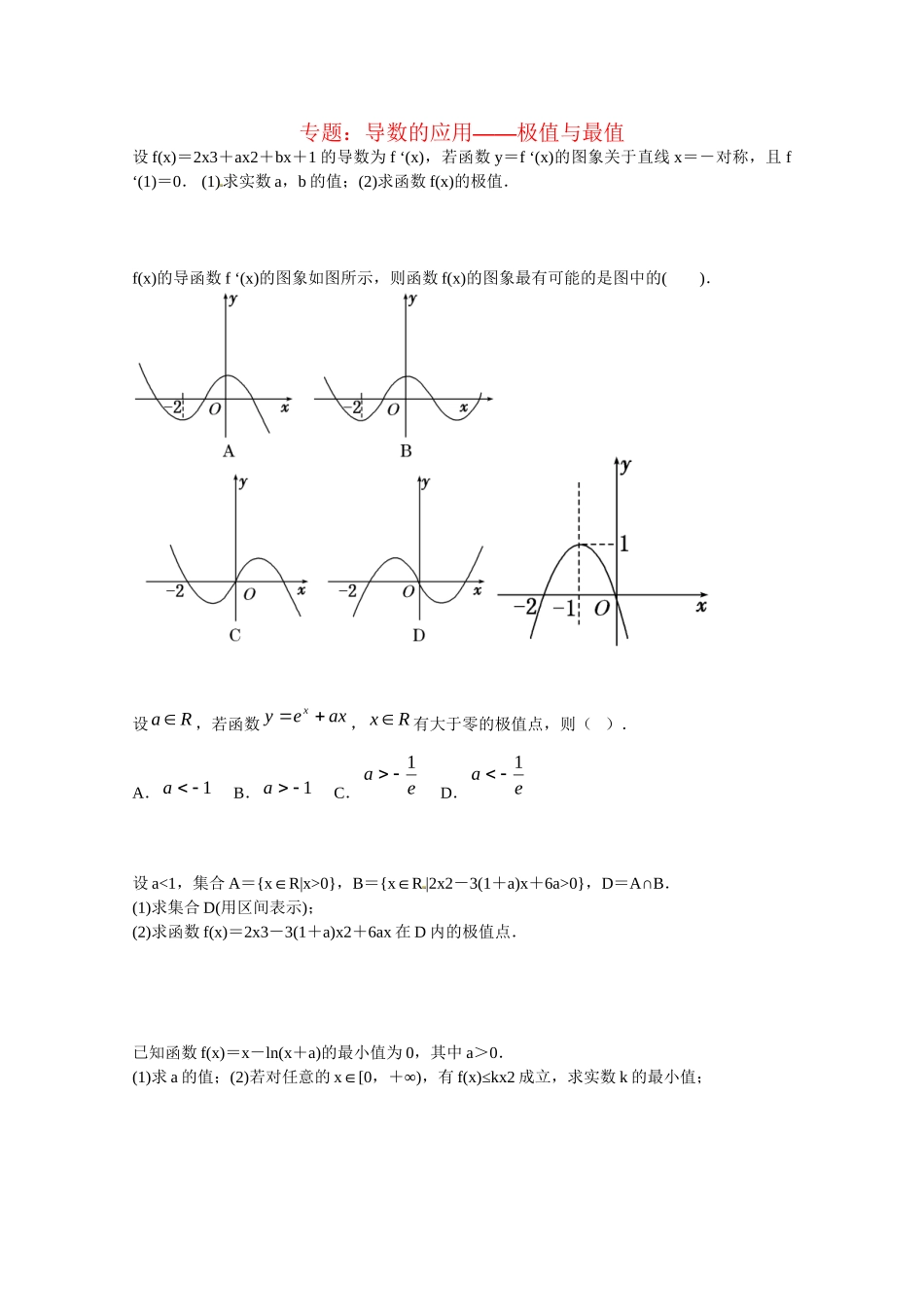
——专题：导数的应用极值与最值设f(x)＝2x3＋ax2＋bx＋1的导数为f‘(x)，若函数y＝f‘(x)的图象关于直线x＝－对称，且f‘(1)＝0．(1)求实数a，b的值；(2)求函数f(x)的极值．f(x)的导函数f‘(x)的图象如图所示，则函数f(x)的图象最有可能的是图中的()．设Ra，若函数axeyx，Rx有大于零的极值点，则（）．A．1aB．1aC．ea1D．ea1设a<1，集合A＝{x∈R|x>0}，B＝{x∈R|2x2－3(1＋a)x＋6a>0}，D＝A∩B．(1)求集合D(用区间表示)；(2)求函数f(x)＝2x3－3(1＋a)x2＋6ax在D内的极值点．已知函数f(x)＝x－ln(x＋a)的最小值为0，其中a＞0．(1)求a的值；(2)若对任意的x∈[0∞，＋)，有f(x)≤kx2成立，求实数k的最小值；已知函数f(x)＝的图象在点(－2，f(－2))处的切线方程为16x＋y＋20＝0．(1)求实数a、b的值；(2)求函数f(x)在区间[－1,2]上的最大值；已知函数f(x)＝x3＋ax2＋(a＋6)x＋1有极大值和极小值，则实数a的取值范围是()．A．－1＜a＜2B．－3＜a＜6C．a＜－3或a＞6D．a＜－1或a＞2课后练习详解答案：(1)a＝3，b＝－12；(2)极大值21，极小值－6．详解：(1)因为f(x)＝2x3＋ax2＋bx＋1，故f‘(x)＝6x2＋2ax＋b．从而f‘(x)＝6＋b－，即y＝f‘(x)的图象关于直线x＝－对称，从而由题设条件知－＝－，解得a＝3．又由于f‘(1)＝0，即6＋2a＋b＝0，解得b＝－12．(2)由(1)知f(x)＝2x3＋3x2－12x＋1，f‘(x)＝6x2＋6x－12＝6(x－1)(x＋2)．令f‘(x)＝0，即6(x－1)(x＋2)＝0，解得x1＝－2，x2＝1．当x∈(∞－，－2)时，f‘(x)＞0，故f(x)在(∞－，－2)上为增函数；当x∈(－2，1)时，f‘(x)＜0，故f(x)在(－2，1)上为减函数；当x∈(1，∞＋)时，f‘(x)＞0，故f(x)在(1∞，＋)上为增函数．从而函数f(x)在x1＝－2处取得极大值f(－2)＝21，在x2＝1处取得极小值f(1)＝－6．答案：A．详解: x∈(∞－，－2)∪(0∞，＋)时f‘(x)<0，∴在(∞－，－2)和(0∞，＋)上f(x)是减函数，排除B、C、D．答案：A．详解： axeyx，∴'xyea．又 函数axeyx有大于零的极值点，即方程'0xyea有大于零的解，即xae(x>0)． x>0时，xe<-1，∴1a．答案：见详解．详解:(1)x∈D⇔x>0且2x2－3(1＋a)x＋6a>0．令h(x)＝2x2－3(1＋a)x＋6a，Δ＝9(1＋a)2－48a＝3(3a－1)(a－3)．①当0，∴B＝R．于是D＝A∩B＝A＝(0∞，＋)．②当a＝时，Δ＝0，此时方程h(x)＝0有唯一解，x1＝x2＝＝＝1，∴B＝(∞－，1)∪(1∞，＋)．于是D＝A∩B＝(0,1)∪(1∞，＋)．③当a<时，Δ>0，此时方程h(x)＝0有两个不同的解x1＝，x2＝． x10，∴B＝(∞－，x1)∪(x2∞，＋)．又 x1>0⇔a>0，所以i)当0a且x1<<1，x2＝＝>＝1，∴a∈D,1∉D．由表可得，x＝a为f(x)在D内的极大值点．④当a≤0时，D＝(x2∞，＋)且x2>1．由表可得，f(x)在D内单调递增．因此f(x)在D内没有极值点．答案：(1)a＝1；(2)．详解:(1)f(x)的定义域为(－a∞，＋)．f‘(x)＝1－＝．由f‘(x)＝0，得x＝1－a＞－a．当x变化时，f‘(x)，f(x)的变化情况如下表：x(－a,1－a)1－a(1－a∞，＋)f‘(x)－0＋f(x)极小值因此，f(x)在x＝1－a处取得最小值，故由题意f(1－a)＝1－a＝0，所以a＝1．(2)当k≤0时，取x＝1，有f(1)＝1－ln2＞0，故k≤0不合题意．当k＞0时，令g(x)＝f(x)－kx2，即g(x)＝x－ln(x＋1)－kx2．g‘(x)＝－2kx＝．令g‘(x)＝0，得x1＝0，x2＝＞－1．①当k≥≤时，0，g‘(x)＜0在(0∞，＋)上恒成立，因此g(x)在[0∞，＋)上单调递减，从而对任意的x∈[0∞，＋)，总有g(x)≤g(0)＝0，即f(x)≤kx2在[0∞，＋)上恒成立，故k≥符合...