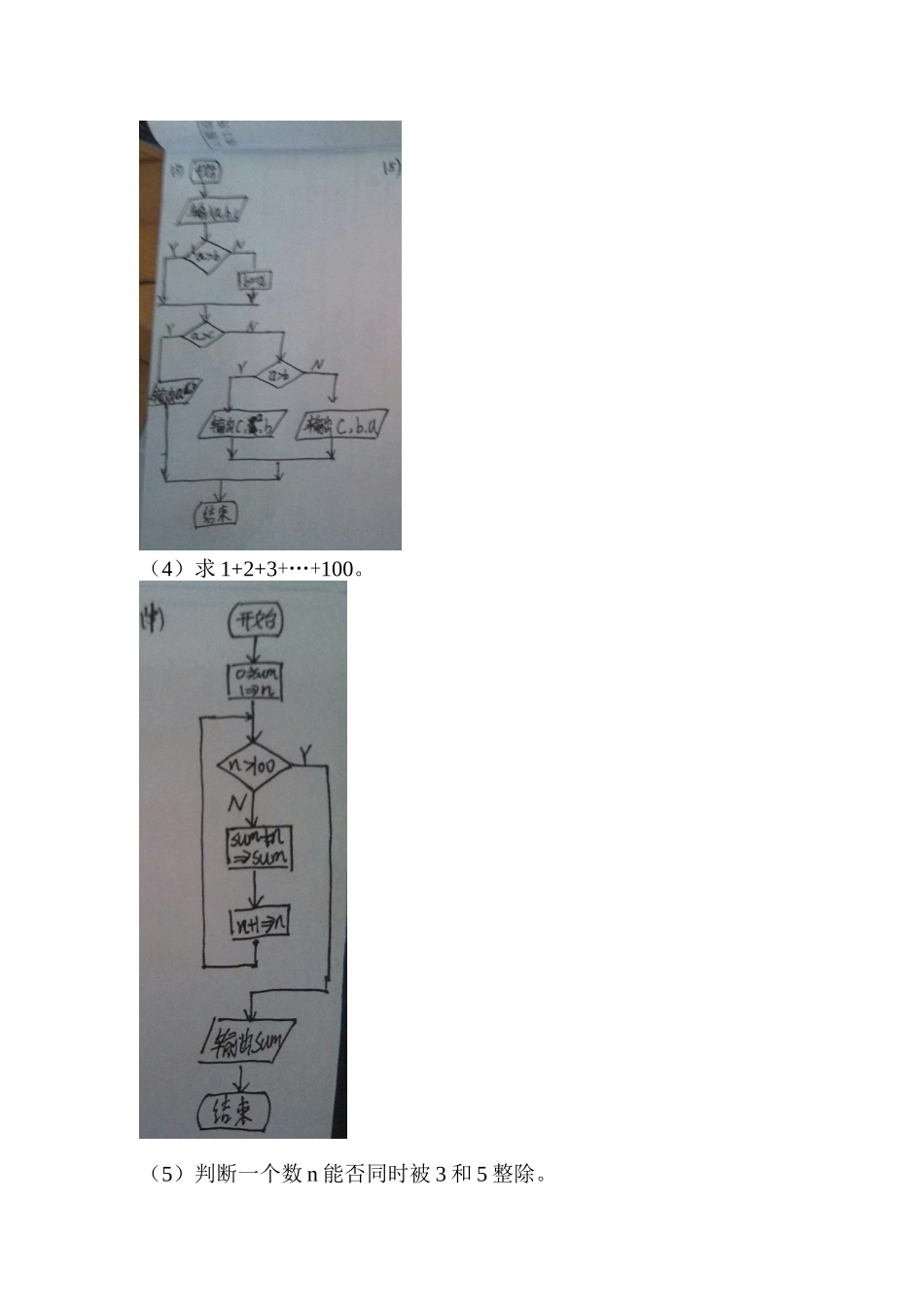
4.用传统流程图表示求解以下问题的算法。(1)有两个瓶子A和B,分别盛放着醋和酱油,要求将它们互换(即A瓶原来盛醋,先改盛酱油,B瓶则相反)。(2)依次将10个数输入,要求输出其中最大的数。(3)有三个数a,b,c,要求按大小顺序把它们输出。(4)求1+2+3+…+100。(5)判断一个数n能否同时被3和5整除。(6)将100~200之间的素数输出。(7)求两个数m和n的最大公约数。(8)求方程式ax^2+bx+c=0的根。分别考虑:①有两个不等的实根。②有两个相等的实根。5.用N—S图表示第四题中各题的算法。(1)(2)(3)A=CB=AC=B1=n输入max当n<10输入aa>maxYNa=maxn+1=n输出max(4)(5)输入a,b,ca>bYNb=aa>cYNa>b输出a,b,cYN输出c,a,b输出c,b,a0=sum,1=n当n<=100sum+n=sumn+1=n输出sum(6)(7)输入nn被3整除YNn被5整除YN输出n:能输出n:不能输出n:不能被3,5整除被3,5整除被3,5整除100=n2=i当i<=n的开方n能被i整除YNn=ii+1=ii200(8)x输入m,nm>nYNm=n当r不等于0n=mr=nm/n的余数=r输出最大公约数n输入a,b,c△=b*b—4ac△>=0YN△=0p=-b/2aYNQ=√-/2a△输出的输出X1=X2X1=(-b+√)/2a△输出=-b/2aX2=(-b-√)/2aX1=p+Qi△输出X1,X2X2=p-Qi8.用自顶向下、逐步细化的方法进行以下算法的设计:(1)输出1900~2000年中是闰年的年份,符合下面两个条件之一的年份是闰年:①能被4整除但不能被100整除;(2)求ax^2+bx+c=0的根。分别考虑△=b*b—4ac大于0、等于0和小于0这三种情况。对year=1900~2000如果year是闰年,则输出year是闰年YN输出yearyear+1=yearyear/4的余数是零且year/100的余数不是零YN输出yearyear/100的余数是零且year/400的余数是零YN输出yearA1对A1细化左边是B1右边是C1对B1细化左边是C2右边是C3对C1细化输入a,b,c△=b*b—4ac根据△的值分别进行处理△>=0YN输出两个实根输出两个复根△=0YN输出两个输出两个相等的实根不相等的实根对C2细化对C3细化(3)输入10个数,输出其中最大的一个数。p=-b/2aQ=√-/2a△输出X1=p+QiX2=p–QiX1=X2=-b/2a输出X1,X2X1=(-b+√)/2a△X2=(-b-√)/2a△输出X1,X2输入10个数找出值最大者输出最大者取一个数给max对其余9个数取一个数给a比较a与max,将较大者保存在max中输出max输入maxn=1当n<10取一个数给aa>maxYNmax=an=n+1输出max