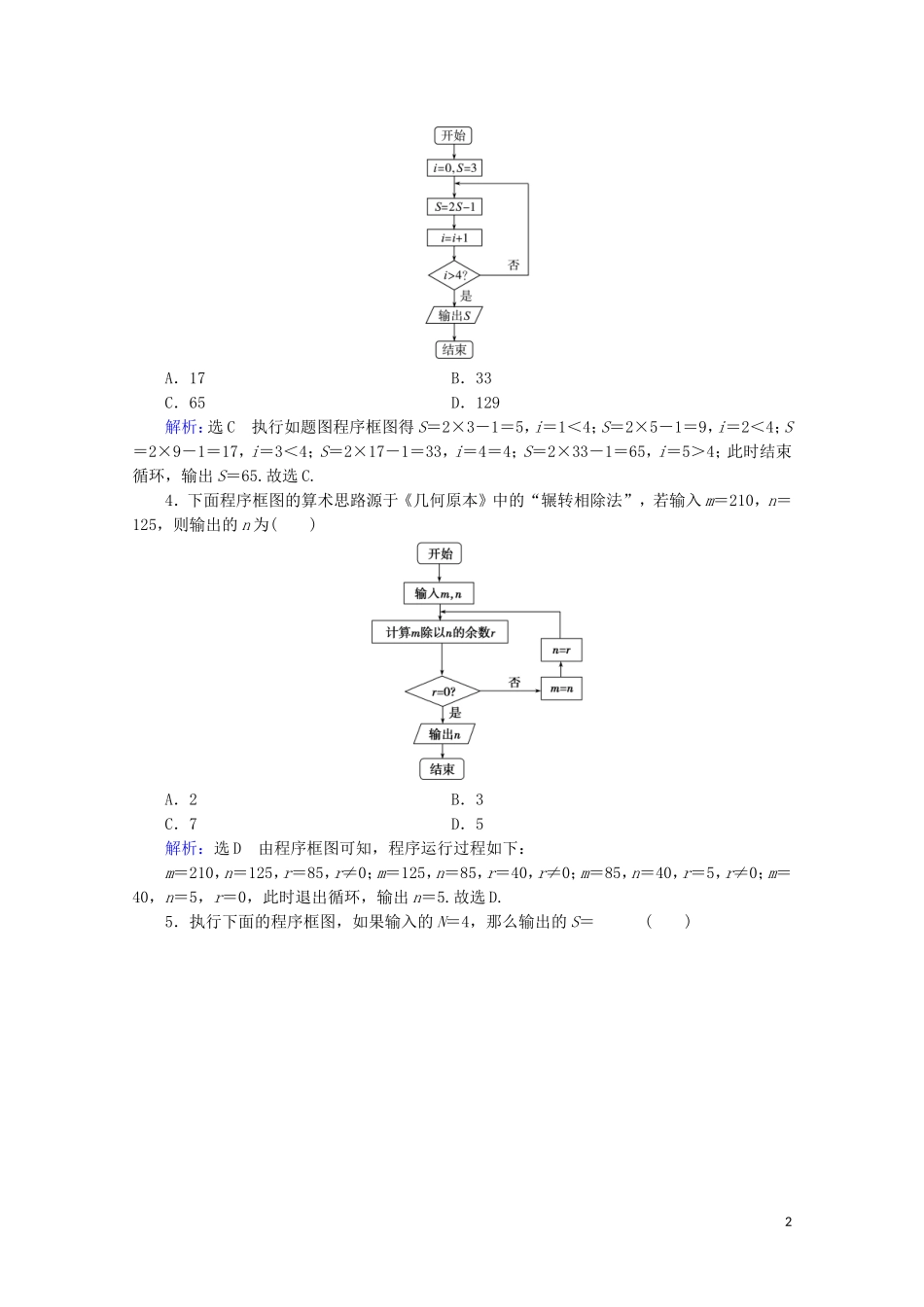
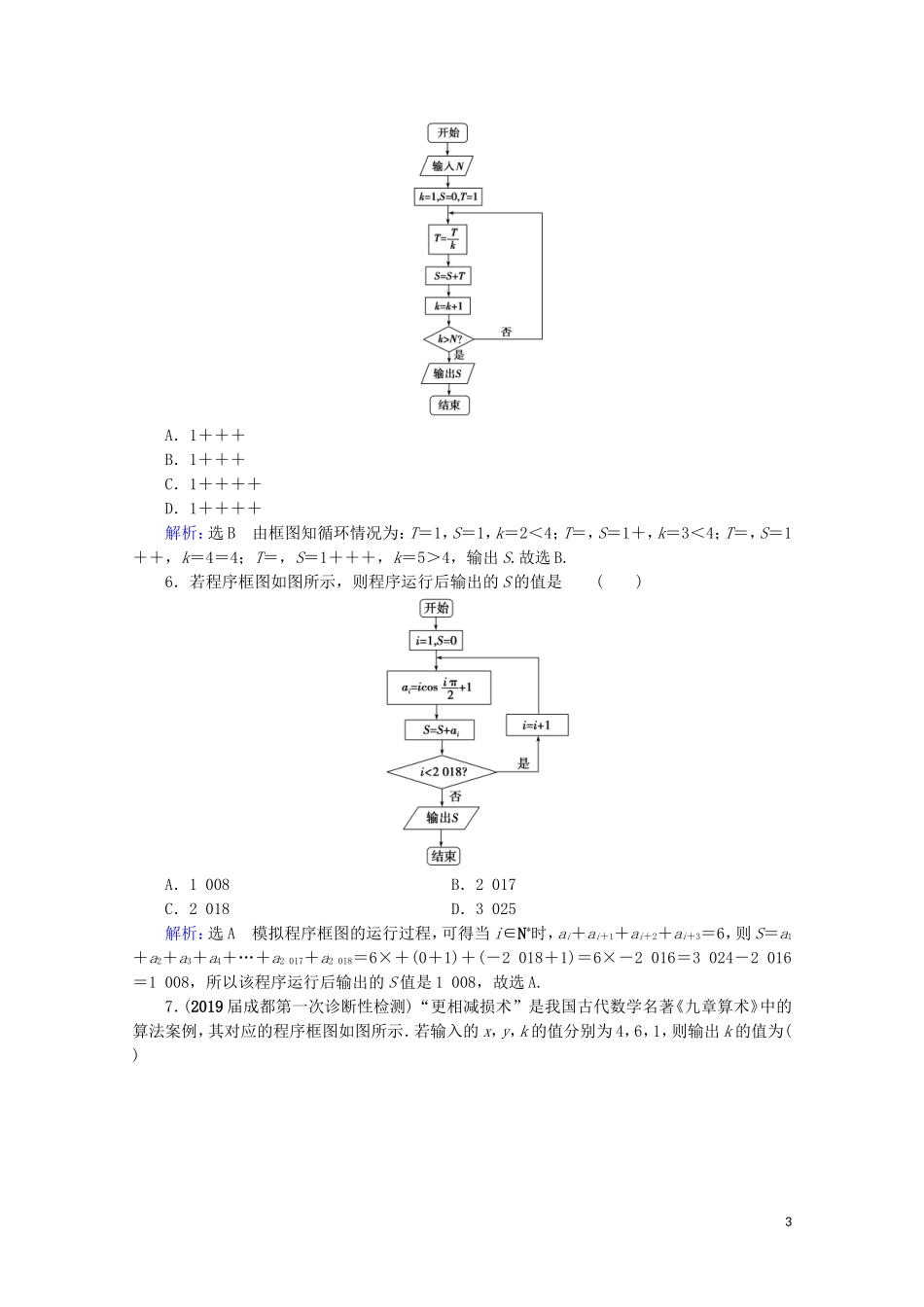
第二节算法与程序框图A级·基础过关|固根基|1.已知一个算法的程序框图如图所示,当输出的结果为0时,输入的实数x的值为()A.-3B.-3或9C.3或-9D.-3或-9解析:选B当x≤0时,-8=0,x=-3;当x>0时,2-log3x=0,x=9.故x=-3或x=9,故选B.2.(2019届石家庄模拟)执行如图所示的程序框图,若输入的a的值为1,则输出的k的值为()A.1B.2C.3D.4解析:选D开始,k=0,a=1,所以b=1,a=-=-,此时a≠b;第一次循环,k=2,a=-=-2,此时a≠b;第二次循环,k=4,a=-=1,此时a=b,结束循环,输出k的值为4,故选D.3.执行如图所示的程序框图,则输出的S的值为()1A.17B.33C.65D.129解析:选C执行如题图程序框图得S=2×3-1=5,i=1<4;S=2×5-1=9,i=2<4;S=2×9-1=17,i=3<4;S=2×17-1=33,i=4=4;S=2×33-1=65,i=5>4;此时结束循环,输出S=65.故选C.4.下面程序框图的算术思路源于《几何原本》中的“辗转相除法”,若输入m=210,n=125,则输出的n为()A.2B.3C.7D.5解析:选D由程序框图可知,程序运行过程如下:m=210,n=125,r=85,r≠0;m=125,n=85,r=40,r≠0;m=85,n=40,r=5,r≠0;m=40,n=5,r=0,此时退出循环,输出n=5.故选D.5.执行下面的程序框图,如果输入的N=4,那么输出的S=()2A.1+++B.1+++C.1++++D.1++++解析:选B由框图知循环情况为:T=1,S=1,k=2<4;T=,S=1+,k=3<4;T=,S=1++,k=4=4;T=,S=1+++,k=5>4,输出S.故选B.6.若程序框图如图所示,则程序运行后输出的S的值是()A.1008B.2017C.2018D.3025解析:选A模拟程序框图的运行过程,可得当i∈N*时,ai+ai+1+ai+2+ai+3=6,则S=a1+a2+a3+a4+…+a2017+a2018=6×+(0+1)+(-2018+1)=6×-2016=3024-2016=1008,所以该程序运行后输出的S值是1008,故选A.7.(2019届成都第一次诊断性检测)“更相减损术”是我国古代数学名著《九章算术》中的算法案例,其对应的程序框图如图所示.若输入的x,y,k的值分别为4,6,1,则输出k的值为()3A.2B.3C.4D.5解析:选C执行程序框图,x=4,y=6,k=1,k=k+1=2,x>y不成立,x=y不成立,y=y-x=2;k=k+1=3,x>y成立,x=x-y=4-2=2;k=k+1=4,x>y不成立,x=y成立,输出k=4.8.(2019届陕西质量检测)若程序框图如图所示,则该程序运行后输出k的值是()A.5B.6C.7D.8解析:选A执行程序框图,n=5,n为奇数,则n=3×5+1=16,k=1,不满足n=1;n=16,n为偶数,则n=8,k=2,不满足n=1;n=8,n为偶数,则n=4,k=3,不满足n=1;n=4,n为偶数,则n=2,k=4,不满足n=1;n=2,n为偶数,则n=1,k=5,退出循环.故输出的k的值是5,故选A.9.秦九韶是我国南宋时期著名的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为3,每次输入a的值均为4,输出S的值为484,则输入n的值可为()4A.6B.5C.4D.3解析:选C模拟程序的运行,可得x=3,k=0,S=0,执行循环体,a=4,S=4,k=1,不满足条件k>n;执行循环体,a=4,S=16,k=2,不满足条件k>n;执行循环体,a=4,S=52,k=3,不满足条件k>n;执行循环体,a=4,S=160,k=4,不满足条件k>n;执行循环体,a=4,S=484,k=5,由题意,此时应该满足条件k>n,退出循环,输出S的值为484,可得5>n≥4,所以输入n的值可为4.故选C.10.(2019届陕西质量检测)执行如图所示的程序框图,设输出的数据构成的集合为A,从集合A中任取一个元素a,则函数y=xa,x∈[0,+∞)是增函数的概率为()A.B.C.D.解析:选C执行程序框图,x=-3,y=3,x=-2<3;y=0,x=-1<3;y=-1,x=0<3;y=0,x=1<3;y=3,x=2<3;y=8,x=3;y=15,x=4>3,退出循环.则集合A中的元素有-1,0,3,8,15,共5个,若函数y=xa,x∈[0,+∞)为增函数,则a>0,所以所求的概率为P=.11.我国古代数学典籍《九章算术...