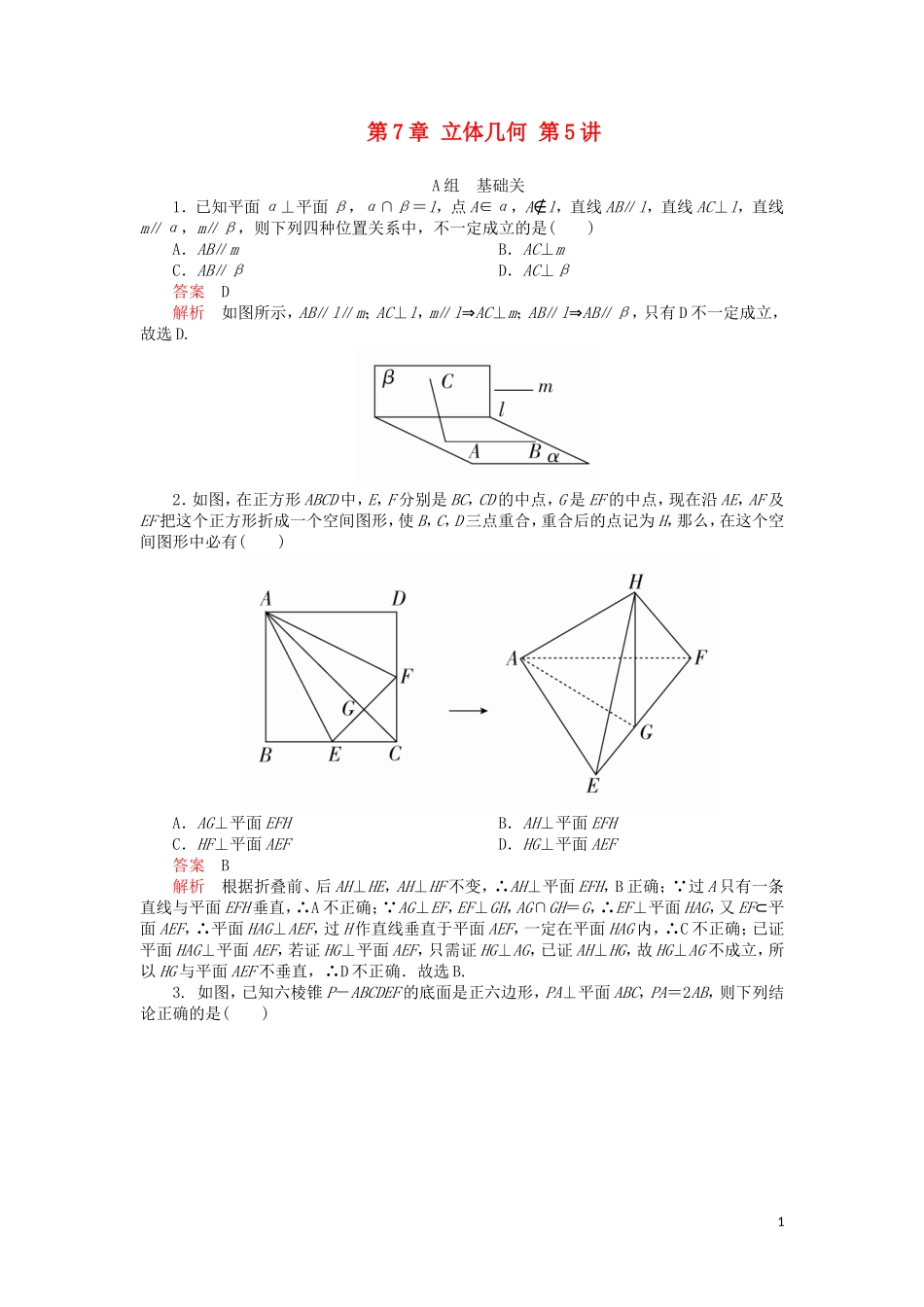
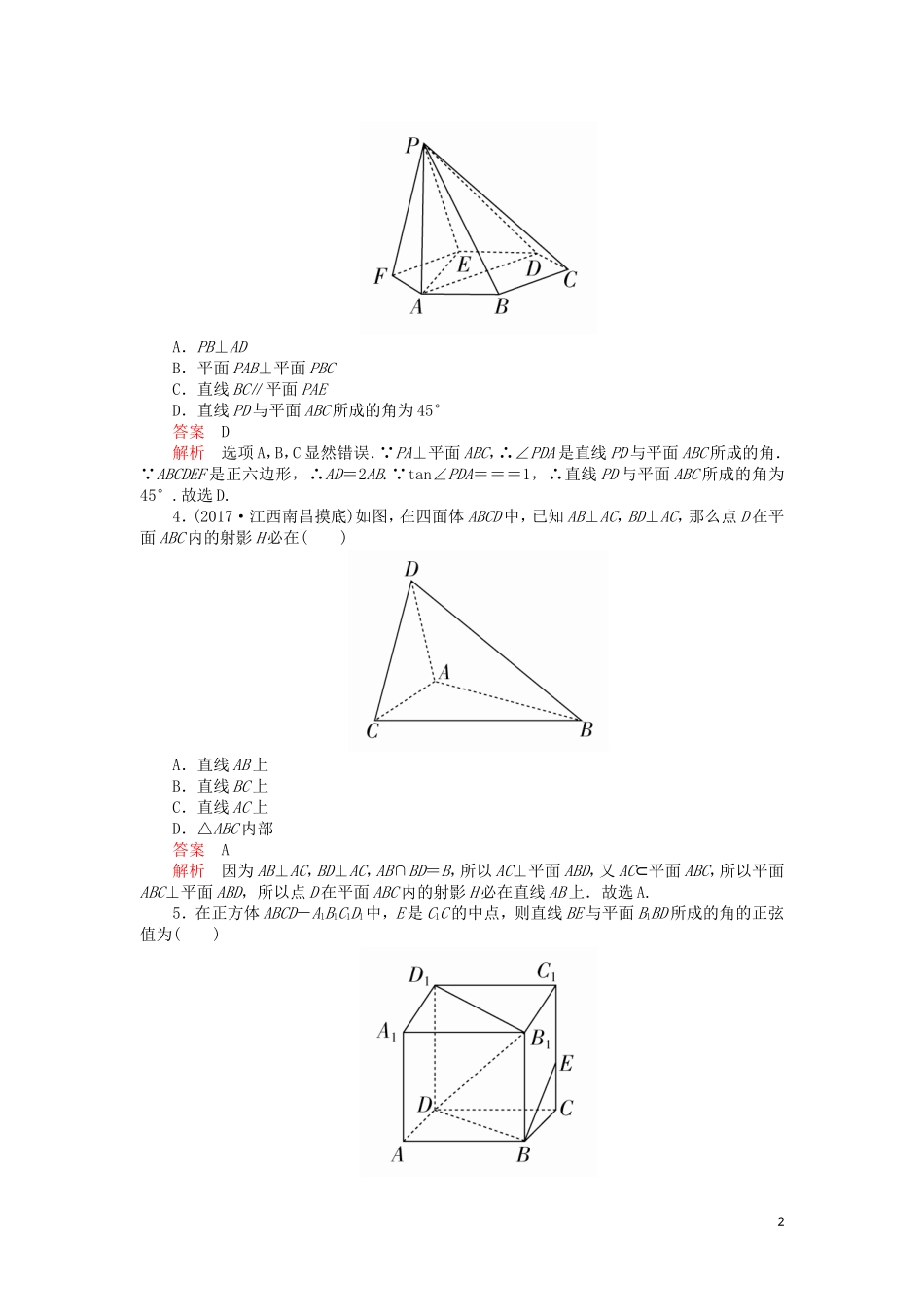
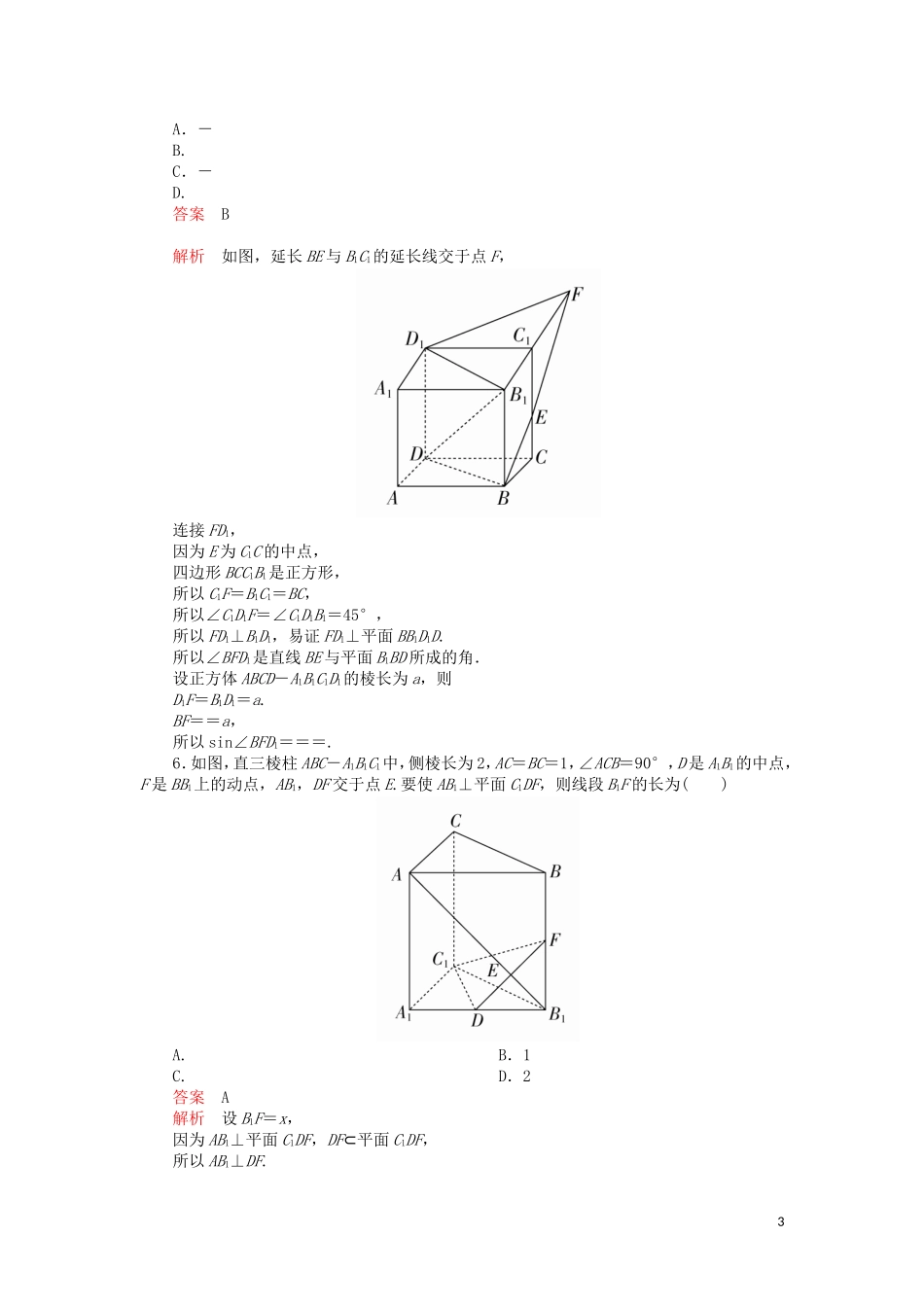
第7章立体几何第5讲A组基础关1.已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是()A.AB∥mB.AC⊥mC.AB∥βD.AC⊥β答案D解析如图所示,AB∥l∥m;AC⊥l,m∥l⇒AC⊥m;AB∥l⇒AB∥β,只有D不一定成立,故选D.2.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,那么,在这个空间图形中必有()A.AG⊥平面EFHB.AH⊥平面EFHC.HF⊥平面AEFD.HG⊥平面AEF答案B解析根据折叠前、后AH⊥HE,AH⊥HF不变,∴AH⊥平面EFH,B正确; 过A只有一条直线与平面EFH垂直,∴A不正确; AG⊥EF,EF⊥GH,AG∩GH=G,∴EF⊥平面HAG,又EF⊂平面AEF,∴平面HAG⊥AEF,过H作直线垂直于平面AEF,一定在平面HAG内,∴C不正确;已证平面HAG⊥平面AEF,若证HG⊥平面AEF,只需证HG⊥AG,已证AH⊥HG,故HG⊥AG不成立,所以HG与平面AEF不垂直,∴D不正确.故选B.3.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是()1A.PB⊥ADB.平面PAB⊥平面PBCC.直线BC∥平面PAED.直线PD与平面ABC所成的角为45°答案D解析选项A,B,C显然错误. PA⊥平面ABC,∴∠PDA是直线PD与平面ABC所成的角. ABCDEF是正六边形,∴AD=2AB. tan∠PDA===1,∴直线PD与平面ABC所成的角为45°.故选D.4.(2017·江西南昌摸底)如图,在四面体ABCD中,已知AB⊥AC,BD⊥AC,那么点D在平面ABC内的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部答案A解析因为AB⊥AC,BD⊥AC,AB∩BD=B,所以AC⊥平面ABD,又AC⊂平面ABC,所以平面ABC⊥平面ABD,所以点D在平面ABC内的射影H必在直线AB上.故选A.5.在正方体ABCD-A1B1C1D1中,E是C1C的中点,则直线BE与平面B1BD所成的角的正弦值为()2A.-B.C.-D.答案B解析如图,延长BE与B1C1的延长线交于点F,连接FD1,因为E为C1C的中点,四边形BCC1B1是正方形,所以C1F=B1C1=BC,所以∠C1D1F=∠C1D1B1=45°,所以FD1⊥B1D1,易证FD1⊥平面BB1D1D.所以∠BFD1是直线BE与平面B1BD所成的角.设正方体ABCD-A1B1C1D1的棱长为a,则D1F=B1D1=a.BF==a,所以sin∠BFD1===.6.如图,直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为()A.B.1C.D.2答案A解析设B1F=x,因为AB1⊥平面C1DF,DF⊂平面C1DF,所以AB1⊥DF.3由已知可以得A1B1=,矩形ABB1A1中,tan∠FDB1=,tan∠A1AB1==.又∠FDB1=∠A1AB1,所以=.故B1F=×=.故选A.7.已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:①对于任意给定的点E,存在点F,使得AF⊥A1E;②对于任意给定的点F,存在点E,使得AF⊥A1E;③对于任意给定的点G,存在点F,使得AF⊥B1G;④对于任意给定的点F,存在点G,使得AF⊥B1G.其中正确结论的个数是()A.0B.1C.2D.3答案C解析因为DE⊥平面A1D,根据三垂线定理,对于任意给定的点E,A1E在平面A1D的射影为A1D,所以存在点F,使得AF⊥A1D,所以AF⊥A1E,①正确;如果对于任意给定的点F,存在点E,使得AF⊥A1E;那么AF⊥A1D,又AD1⊥A1D,得到过A有两条直线与A1D垂直,故②错误;只有AF垂直B1G在平面BCC1B1中的射影时,AF⊥B1G,所以当G位于D1B的上半部分时,在D1D上不存在F点,使AF垂直B1G在平面BCC1B1中的射影,③错误;对任意给定的点F,存在平面BCC1B1上的线段B1G′和AF垂直,且B1G′为B1G的投影,所以④正确,所以C正确.8.如图,平面ABC⊥平面BDC,∠BAC=∠BDC=90°,且AB=AC=a,则AD=________.4答案a解析作BC中点E,连接AE,DE,则在Rt△ABC中,AB=AC=a,由勾股定理得BC=2AE=a,且有AE⊥BC,又平面ABC⊥平面BDC,平面ABC∩平面BDC=BC且直线AE在平面ABC内,∴由面面垂直的性质定理得AE⊥平面BCD, DE⊂平面BCD内,∴AE⊥DE,又在Rt△BCD中,点E是BC的中点,∴DE==a,∴在Rt△ADE中,AE=a,由勾股定理得AD==...