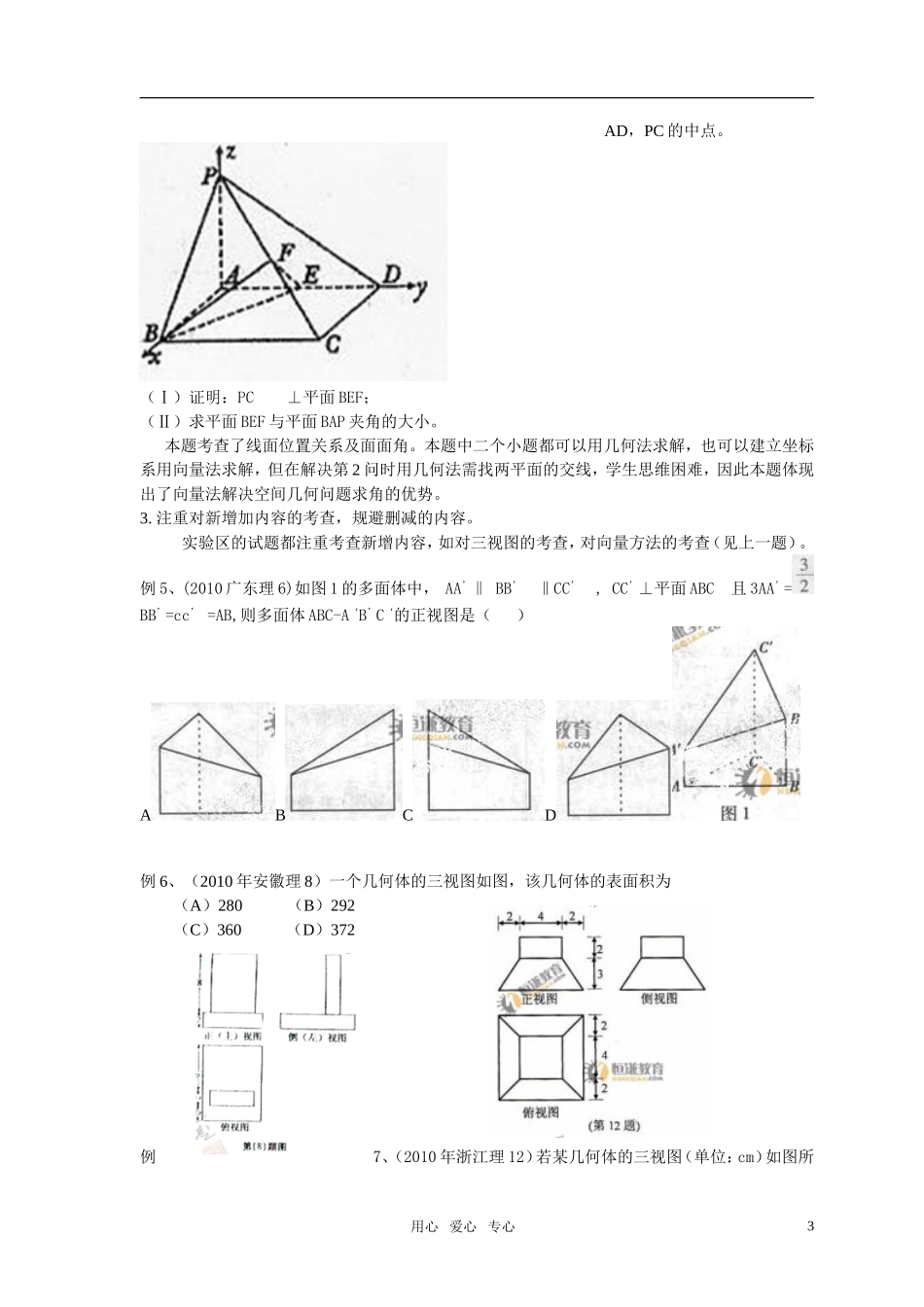
21010年实验区高考试题分析(立体几何、空间向量)《普通高中数学课程标准(实验)》(以下简称课程标准)是普通高中数学教学和高考命题的依据,与大纲相比较课程标准中很多内容及其要求都发生了变化,立体几何是课标中变化较大的内容之一,在教学中如何应对这种变化呢?本文从2010年实验区高考试题的特点分析立体几何教学的方向。一、课标与大纲的区别1.编排方式的变化。在大纲中,立体几何是作为一个整体安排在必修中,而在课标中将立体几何的内容分为3部分,分阶段学习不同的内容。具体编排见下表。大纲课标位置与内容必修(直线、平面、简单几何体)数学2(立体几何初步)选修2—2(推理与证明——反证法)选修2-3(空间向量与立体几何)课时36182122.立体几何的学习作为向量的应用。在大纲中立体几何是在综合几何的观点下进行学习的,在课标中,学生在必修部分学习立体几何初步的知识,立体几何中与位置关系相关的问题是作为向量的应用学习的。3.文理学习的内容差别加大。从上表可以看出,侧重文科的学生只在数学2中学习立体几何初步,之后只在选修1-2“推理与证明”部分学习反证法,就不再学习立体几何。而侧重理科的学生则要在向量的背景下继续学习立体几何,学习直线的方向向量与平面的法向量,运用向量语言表述线线、线面、面面的垂直、平行关系,用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理),用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。可见与大纲相比,课标加强了向量在解决立体几何中的作用。二、实验区高考试题分析:1.对基本关系的考查体现了直观感知和操作确认。例1、(2010年浙江理6)设m,l是两条不同的直线,α是一个平面,则下列命题正确的是()用心爱心专心1这个题目考查了线面基本位置关系的判定,但是其考查的切入点不是知识的再现,而是基于基本知识的分析判断,学生可以根据题目给出的条件用手头的工具进行操作判断,也可以通过想象进行判断。例2、(2010年福建理6)如图,若是长方体ABCD-被平面EFCH截去几何体EFCH后得到的几何体,其中E为线段上异于的点,F为线段上异于的点,且EH//,则下列结论中不正确的是()A.EH//FGB.四边开EFGH是矩形C.是棱柱D.是棱台【新课标要求:借助长方体模型,在直观认识和理解空间点、线、面的位置关系的基础上,抽象出空间线、面位置关系的定义。】这个题目以长方体为载体,认识空间几何体的结构特征,考查线面关系性质定理与判定定理。这些题目的共同特点都是,即考查了基本知识,又考查了学生直观感知、操作确认的能力。2.理科试题主题不变,在解答题中向量方法与综合几何法并重。【新课标要求:学习直线的方向向量与平面的法向量,运用向量语言表述线线、线面、面面的垂直、平行关系,用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理),用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。】可见与大纲相比,课标加强了向量在解决立体几何中的作用。理科试题中的解答题除个别题目之外都可以用向量方法和综合几何法两类方法求解,而且向量方法不但有坐标法,还有几何法。运用向量方法不但可以证明确定的结论,还可以探索未知的结论,从新课程的角度看更加侧重用向量法解决问题。例3、(2010年宁夏海南卷理18)如圈,己知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,⊥BD垂足为H,PH是四棱锥的高,E为AD中点.(Ⅰ)证明:PE⊥BC(Ⅱ)若==60°,求直线PA与平面PEH所成角的正弦值.本题考查了线线、线面位置关系及线面角。本题中二个小题都可以用几何法求解,也可以建立坐标系用向量法求解,或者用向量几何法求解。例4、(2010年陕西理18)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2√2,E,F分别是用心爱心专心2AD,PC的中点。(Ⅰ)证明:PC⊥平面BEF;(Ⅱ)求平面BEF与平面BAP夹角的大小。本题考查了线面位置关系及面面角。本题中二个小题都可以用几何法求解,也可以建立坐标系用向量法求解,但在解决第2问时用几何法需找两平面的交线,学生思维困难,因此本题体现出了向量法解决空间...