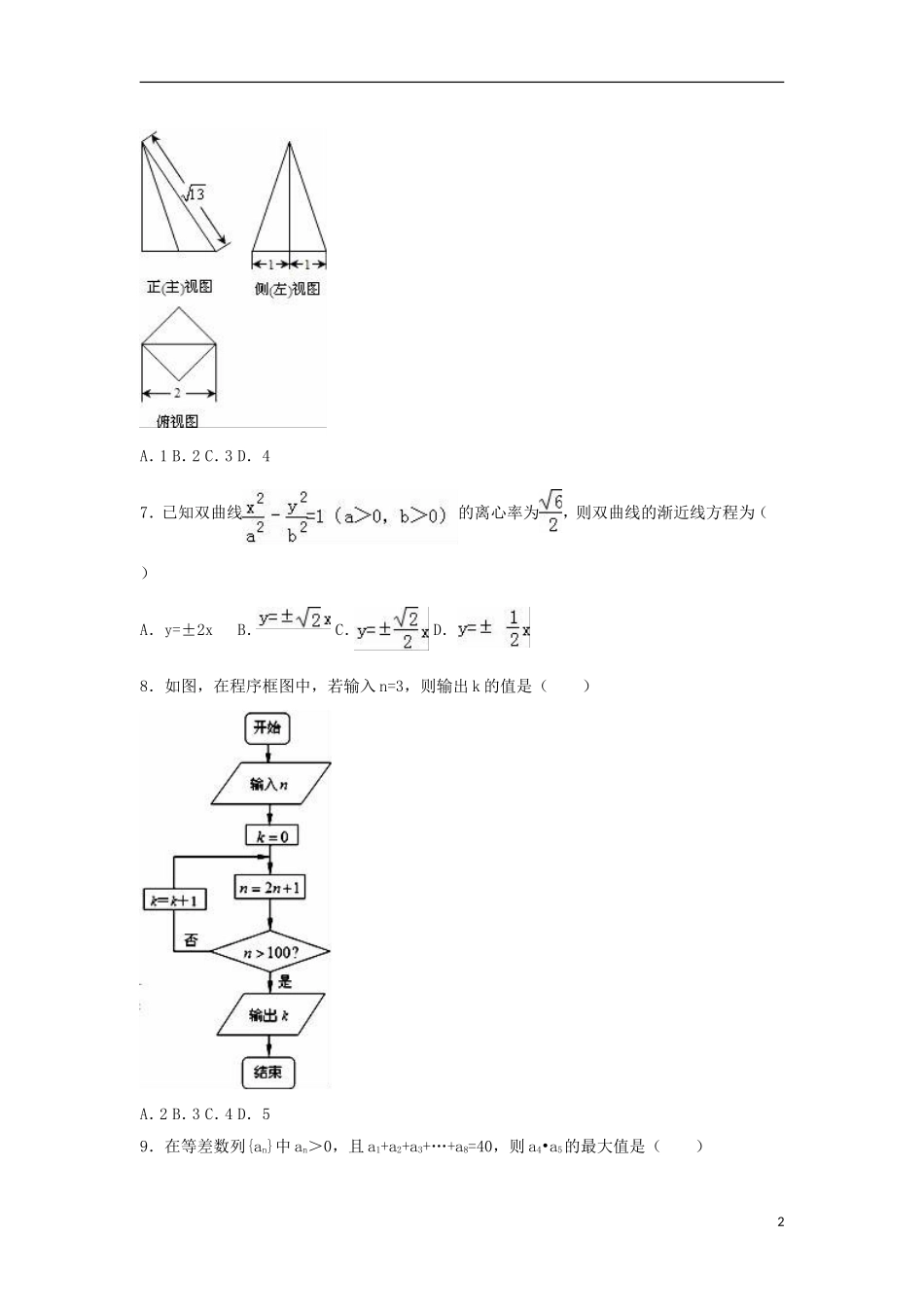
2015年广西南宁市武鸣高中高考数学一模试卷(文科)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合A={x|﹣3<x<3},B={x|x>1},则集合A∩B为()A.[0,3)B.[1,3)C.(1,3)D.(﹣3,1]2.在复平面内,复数对应的点的坐标是()A.(﹣1,1)B.(﹣1,﹣1)C.(1,﹣1)D.(1,1)3.下列有关命题的说法正确的是()A.若“p∧(¬q)”为真命题,则“p∧q”也为真命题B.“x=3”是“2x2﹣7x+3=0”成立的充分不必要条件C.命题“∀x∈R,均有x2﹣x+1>0”的否定是:“∃x∈R,使得x2﹣x+1<0”D.线性回归方程对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点4.棱长为2的正方体ABCD﹣A1B1C1D1的内切球的表面积为()A.B.16πC.4πD.5.已知α∈(,π),sinα=,则tan(α﹣)=()A.﹣7B.﹣C.7D.6.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是()1A.1B.2C.3D.47.已知双曲线的离心率为,则双曲线的渐近线方程为()A.y=±2xB.C.D.8.如图,在程序框图中,若输入n=3,则输出k的值是()A.2B.3C.4D.59.在等差数列{an}中an>0,且a1+a2+a3+…+a8=40,则a4•a5的最大值是()2A.5B.10C.25D.AB=4,5010.已知向量,,若与共线,则m的值为()A.B.2C.D.﹣211.在平面区域内随机取一点,则所取的点恰好落在圆x2+y2=1内的概率是()A.B.C.D.12.定义域为R的可导函数y=f(x)的导函数为f′(x),满足f(x)>f′(x)且f(0)=1,则不等式<1的解为()A.(﹣∞,0)B.(0,+∞)C.(﹣∞,2)D.(2,+∞)二、填空题(本题共4小题,每题5分,共20分)13.如图是甲、乙两名篮球运动员2012年赛季每场比赛得分的茎叶图,则甲、乙两人比赛得分的中位数之和是.14.设函数f(x)=ax3+bx2+cx,若1和﹣1是函数f(x)的两个零点,x1和x2是f(x)的两个极值点,则x1•x2=.15.已知数列{an}:,+,++,+++,…,那么数列bn=前n项和为.316.设抛物线C:y2=3px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.已知向量=(sinx,﹣1),=(cosx,﹣),函数f(x)=()•﹣2.(1)求函数f(x)的最小正周期T;(2)已知a,b,c分别为△ABC内角A,B,C的对边,其中A为锐角,a=2,c=4,且f(A)=1,求A,b和△ABC的面积S.18.某区卫生部门成立了调查小组,调查“常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.(Ⅰ)完成下列2×2列联表,并分析能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?不常吃零食常吃零食总计不患龋齿患龋齿总计(Ⅱ)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.P(K2≥k0)0.0100.0050.001k06.6357.87910.828附:k2=.19.如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.(Ⅰ)证明:PQ∥平面ACD;(Ⅱ)求AD与平面ABE所成角的正弦值.420.已知椭圆+=1(a>b>0)的长轴长为4,且点(1,)在椭圆上.(Ⅰ)求椭圆的方程;(Ⅱ)过椭圆右焦点斜率为k的直线l交椭圆于A,B两点,若•=0,求直线l的方程.21.已知函数f(x)=ln(1+x)﹣,k∈R.(1)讨论f(x)的单调区间;(2)当k=1时,求f(x)在[0,+∞)上的最小值,并证明+++…+<ln(1+n).请考生在第22、23、24题中任选一道作答,如果多做,则按所做的第1题计分.作答时请写清题号.[选修4-1几何证明选讲]22.已知△ABC中,AB=AC,D为△ABC外接圆劣弧上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F(1)求证:∠CDF=∠EDF;(2)求证:AB•AC•DF=...