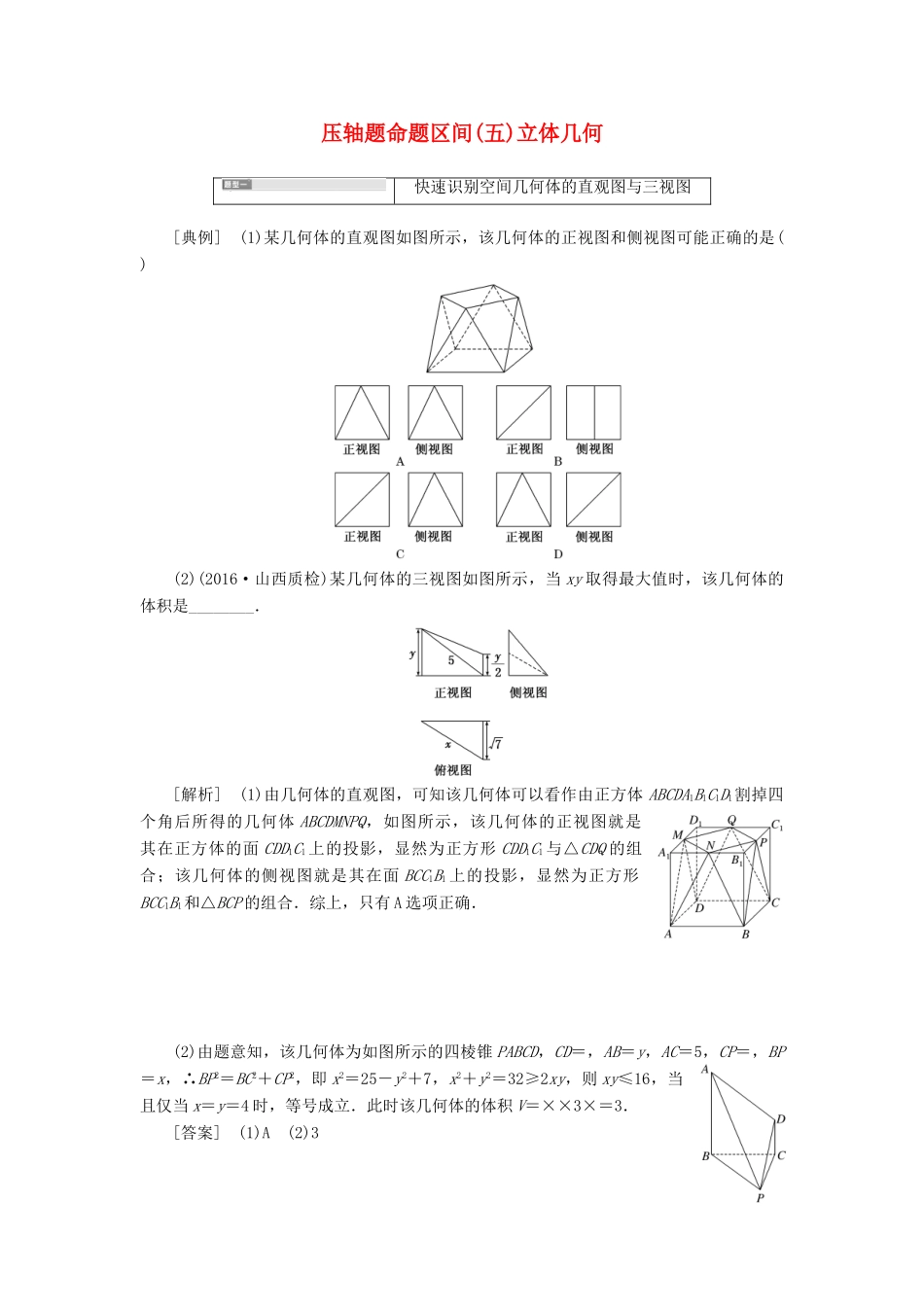
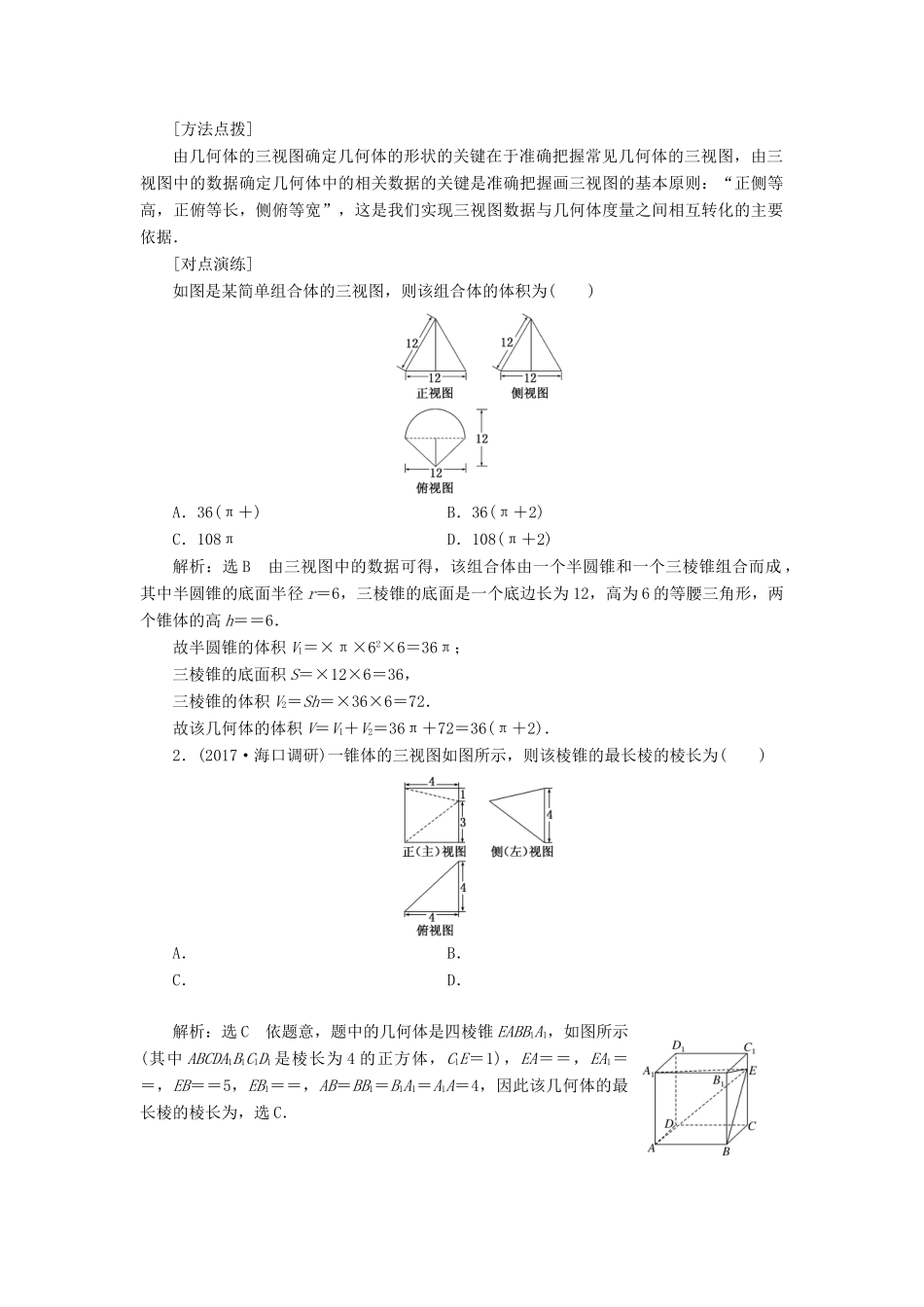
压轴题命题区间(五)立体几何快速识别空间几何体的直观图与三视图[典例](1)某几何体的直观图如图所示,该几何体的正视图和侧视图可能正确的是()(2)(2016·山西质检)某几何体的三视图如图所示,当xy取得最大值时,该几何体的体积是________.[解析](1)由几何体的直观图,可知该几何体可以看作由正方体ABCDA1B1C1D1割掉四个角后所得的几何体ABCDMNPQ,如图所示,该几何体的正视图就是其在正方体的面CDD1C1上的投影,显然为正方形CDD1C1与△CDQ的组合;该几何体的侧视图就是其在面BCC1B1上的投影,显然为正方形BCC1B1和△BCP的组合.综上,只有A选项正确.(2)由题意知,该几何体为如图所示的四棱锥PABCD,CD=,AB=y,AC=5,CP=,BP=x,∴BP2=BC2+CP2,即x2=25-y2+7,x2+y2=32≥2xy,则xy≤16,当且仅当x=y=4时,等号成立.此时该几何体的体积V=××3×=3.[答案](1)A(2)3[方法点拨]由几何体的三视图确定几何体的形状的关键在于准确把握常见几何体的三视图,由三视图中的数据确定几何体中的相关数据的关键是准确把握画三视图的基本原则:“正侧等高,正俯等长,侧俯等宽”,这是我们实现三视图数据与几何体度量之间相互转化的主要依据.[对点演练]如图是某简单组合体的三视图,则该组合体的体积为()A.36(π+)B.36(π+2)C.108πD.108(π+2)解析:选B由三视图中的数据可得,该组合体由一个半圆锥和一个三棱锥组合而成,其中半圆锥的底面半径r=6,三棱锥的底面是一个底边长为12,高为6的等腰三角形,两个锥体的高h==6.故半圆锥的体积V1=×π×62×6=36π;三棱锥的底面积S=×12×6=36,三棱锥的体积V2=Sh=×36×6=72.故该几何体的体积V=V1+V2=36π+72=36(π+2).2.(2017·海口调研)一锥体的三视图如图所示,则该棱锥的最长棱的棱长为()A.B.C.D.解析:选C依题意,题中的几何体是四棱锥EABB1A1,如图所示(其中ABCDA1B1C1D1是棱长为4的正方体,C1E=1),EA==,EA1==,EB==5,EB1==,AB=BB1=B1A1=A1A=4,因此该几何体的最长棱的棱长为,选C.与球相关的“接”、“切”问题[典例](1)某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的体积为()A.B.3πC.D.π(2)若圆锥的内切球与外接球的球心重合,且内切球的半径为1,则圆锥的体积为________.(3)若正三棱锥的高和底面边长都等于6,则其外接球的表面积为________.[解析](1)把该四面体ABCD放入正方体中,如图所示,此四面体的外接球即为正方体的外接球,由题意可知,正方体的棱长为1,所以外接球的半径为R=,所以此四面体的外接球的体积为V=×π×3=π.故选C.(2)过圆锥的旋转轴作轴截面,得△ABC及其内切圆⊙O1和外切圆⊙O2,且两圆同圆心,即△ABC的内心与外心重合,易得△ABC为正三角形,由题意知⊙O1的半径为r=1,△ABC的边长为2,于是知圆锥的底面半径为,高为3.故所求体积为V=×π×3×3=3π.(3)如图,作PM⊥平面ABC于点M,则球心O在PM上,PM=6,连接AM,AO,则OP=OA=R,在Rt△OAM中,OM=6-R,OA=R,又AB=6,且△ABC为等边三角形,故AM==2,则R2-(6-R)2=(2)2,解得R=4,所以球的表面积S=4πR2=64π.[答案](1)C(2)3π(3)64π[方法点拨]与球相关的“接”、“切”问题的解决方法方法解读适合题型截面法解答时首先要找准切点,通过作截面来球内切多面体或旋转体(如典例(2))解决.如果内切的是多面体,则作截面时主要抓住多面体过球心的对角面来作构造直角三角形法首先确定球心位置,借助外接的性质——球心到多面体的顶点的距离等于球的半径,寻求球心到底面中心的距离、半径、顶点到底面中心的距离构造成直角三角形,利用勾股定理求半径正棱锥、正棱柱的外接球(如典例(3))补形法因正方体、长方体的外接球半径易求得,故将一些特殊的几何体补形为正方体或长方体,便可借助外接球为同一个的特点求解三条侧棱两两垂直的三棱锥,从正方体或长方体的八个顶点中选取点作为顶点组成的三棱锥、四棱锥等(如典例(1))[对点演练]1.一个正六棱柱的所有顶点在同一个球面上,且这个正六棱柱的底面周长为6,体积为,那么...