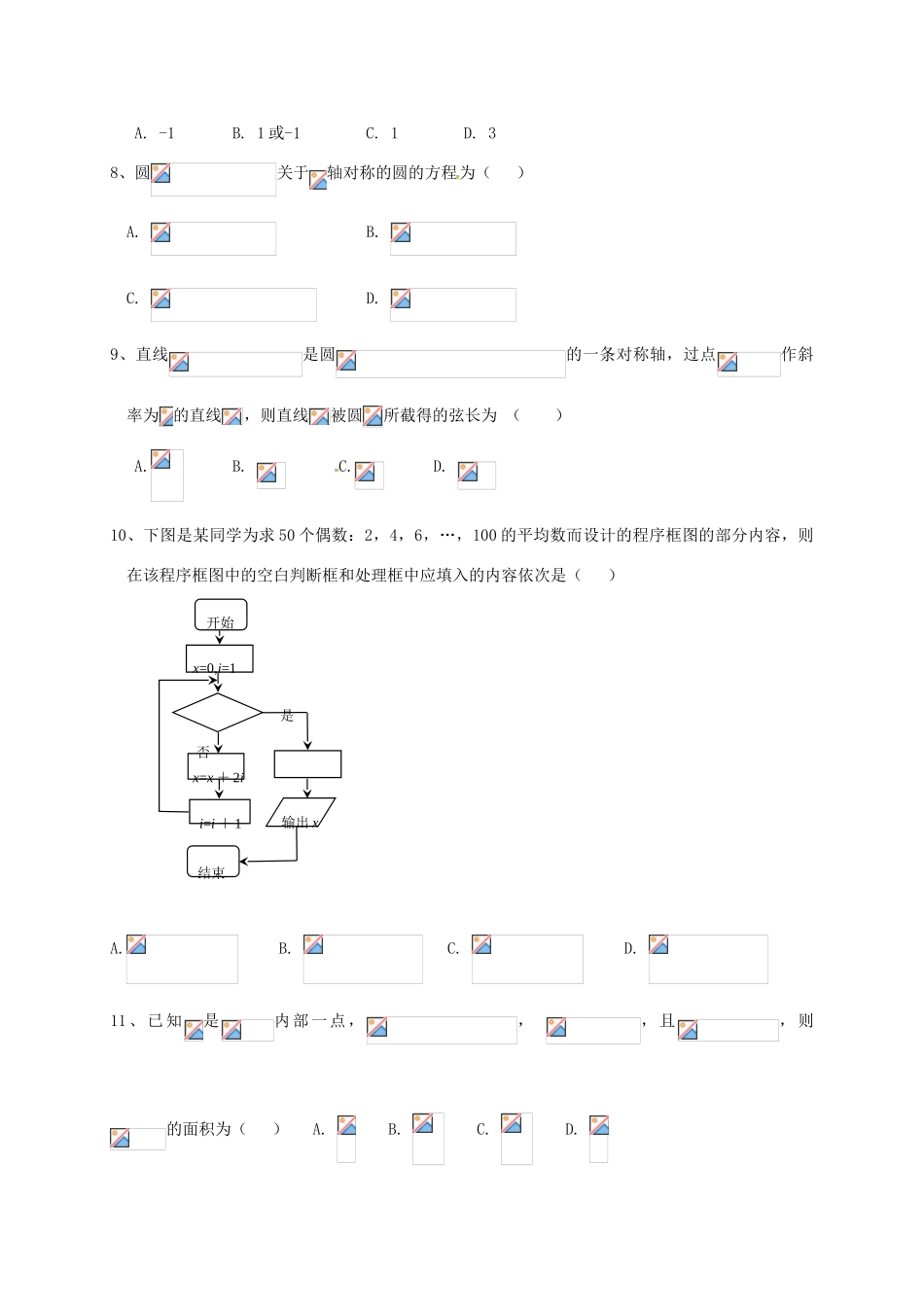
辽宁省瓦房店市2016-2017学年高一数学6月基础知识竞赛试题一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1、设全集,,,则()A.B.C.D.2、下列函数中,既是偶函数又在区间上单调递减的是()A.B.C.D.3、已知实数满足,,则函数的零点个数是()A.0B.1C.2D.34、已知函数的图象与函数()的图象交于点,如果,那么的取值范围是()A.B.C.D.5、设,则、、的大小关系是()A.B.C.D.6、已知,是两条不同直线,是一个平面,则下列命题中正确的是()A.若,,则B.若,,则C.若,,则D.若,,则7、若直线与直线平行,则的值为()A.-1B.1或-1C.1D.38、圆关于轴对称的圆的方程为()A.B.C.D.9、直线是圆的一条对称轴,过点作斜率为的直线,则直线被圆所截得的弦长为()A.B.C.D.10、下图是某同学为求50个偶数:2,4,6,…,100的平均数而设计的程序框图的部分内容,则在该程序框图中的空白判断框和处理框中应填入的内容依次是()A.B.C.D.11、已知是内部一点,,,且,则的面积为()A.B.C.D.开始x=0,i=1是结束否x=x+2ii=i+1输出x12、若,且,则的值为()A.B.C.D.二.填空题:本大题共4小题,每小题5分13、化简.14、下列叙述:①函数是奇函数;②函数的一条对称轴方程为;③函数,,则的值域为;④函数,有最小值,无最大值.所有正确结论的序号是__________.15、已知向量,,若,则_________.16、设的内角所对的边长分别为,且,则的值为__________.三.解答题:解答应写出文字说明,证明过程或演算步骤.17、已知集合,集合,(1)求;(2)若集合满足求实数的取值范围.18、在中,三个内角分别为,已知.(1)求角的值;(2)若,且,求.19、如图,在三棱柱中,面,,在线段上,,.(1)求证:;(2)试探究:在上是否存在点,满足∥平面,若存在,请指出点的位置,并给出证明;若不存在,说明理由.20、某种产品的广告费支出与销售额(单位:万元)之间有如下对应数据:245683040605070(1)求回归直线方程;(2)预测广告费支出为10万元时,销售额多大?(,)21、的内角的对边分别为,已知.(1)求;(2)若,求的面积的最大值.22、已知圆,是轴上的动点,分别切圆于两点.(1)若,求及直线的方程;(2)求证:直线恒过定点.答案CBBDBCCACABC13、114、②④15、16、4三.17、解:(1)依题意有(2)18、解:(1)因为,得,即,因为,且,所以,所以.(2)因为,所以,因为,所以,所以.19、解:(1)∵AA1⊥面ABC,BC?面ABC,∴BC⊥AA1.又∵BC⊥AC,AA1,AC?面AA1C1C,AA1∩AC=A,∴BC⊥面AA1C1C,又AC1?面AA1C1C,∴BC⊥AC1.(2)(法一)当AF=3FC时,FE∥平面A1ABB1.理由如下:在平面A1B1C1内过E作EG∥A1C1交A1B1于G,连结AG.∵B1E=3EC1,∴EG=43A1C1,又AF∥A1C1且AF=43A1C1,∴AF∥EG且AF=EG,∴四边形AFEG为平行四边形,∴EF∥AG,又EF?面A1ABB1,AG?面A1ABB1,∴EF∥平面A1ABB1.(法二)当AF=3FC时,FE∥平面A1ABB1.理由如下:在平面BCC1B1内过E作EG∥BB1交BC于G,连结FG.∵EG∥BB1,EG?面A1ABB1,BB1?面A1ABB1,∴EG∥平面A1ABB1.∵B1E=3EC1,∴BG=3GC,∴FG∥AB,又AB?面A1ABB1,FG?面A1ABB1,∴FG∥平面A1ABB1.又EG?面EFG,FG?面EFG,EG∩FG=G,∴平面EFG∥平面A1ABB1.∵EF?面EFG,∴EF∥平面A1ABB1.20、解:(1),,∴,.因此,所求回归直线方程为.(2)根据上面求得的回归直线方程,当广告费支出为10万元时,(万元),即这种产品的销售收入大约为82.5万元.21、解:(1)由已知及正弦定理可得,在中,,∴,∴,从而,∵,∴,∴,∴;(2)解法:由(1)知,∴,∵,∴,∵,∴,∵,∴(当且仅当时等号成立),∴;解法二:由正弦定理可知,∵,∴,∴,∴,∵,∴,∴当,即时,取最大值.22、解:(1)设直线则,又,∴,∴设,而点由得,则或,从而直线的方程为:或.(2)证明:设点,由几何性质可以知道,在以为直径的圆上,此圆的方程为,为两圆的公共弦,两圆方程相减得即过定点.