高考数学 数形结合思想在中的运用知识点分析 北师大版VIP免费

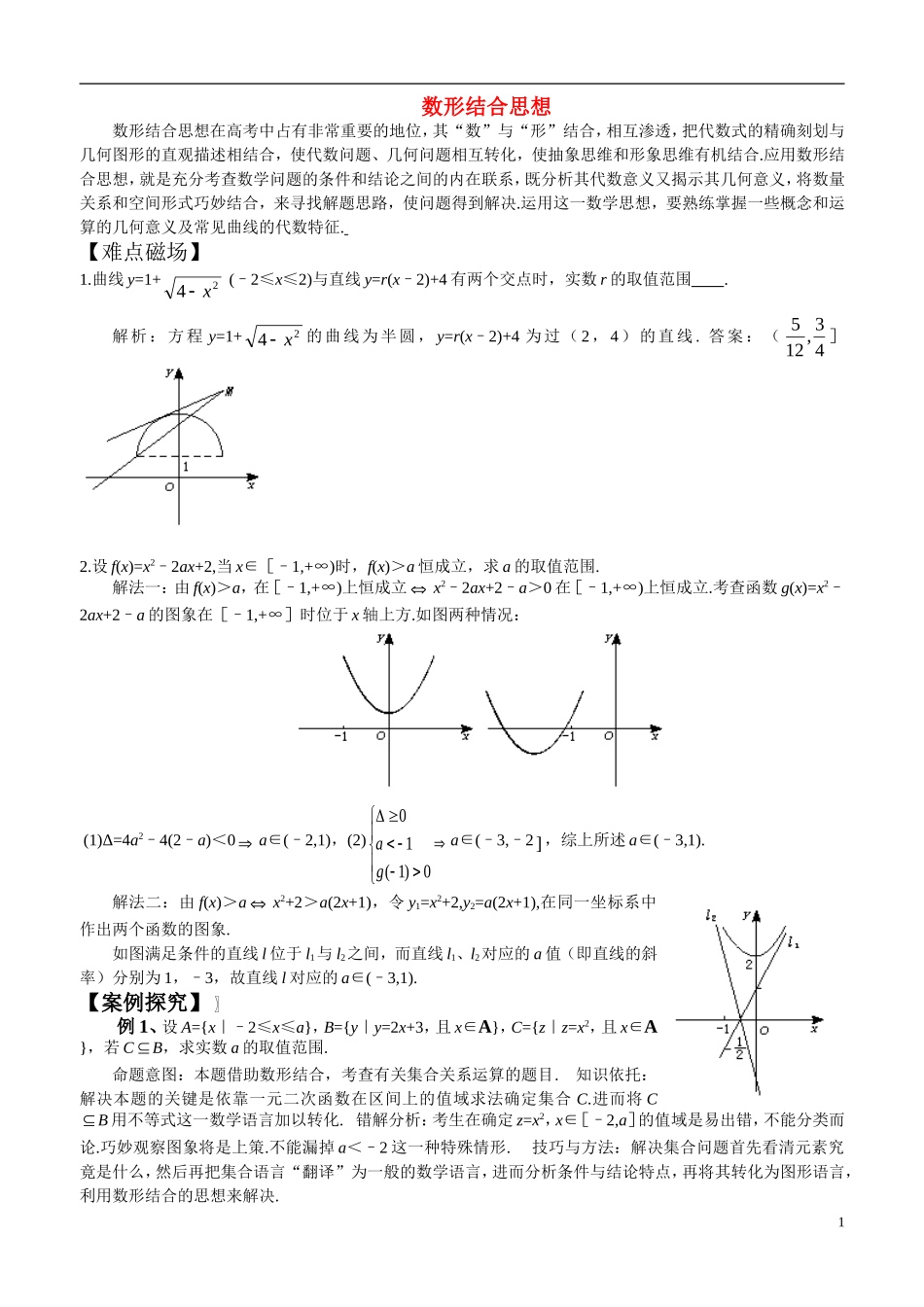
数形结合思想数形结合思想在高考中占有非常重要的地位，其“数”与“形”结合，相互渗透，把代数式的精确刻划与几何图形的直观描述相结合，使代数问题、几何问题相互转化，使抽象思维和形象思维有机结合.应用数形结合思想，就是充分考查数学问题的条件和结论之间的内在联系，既分析其代数意义又揭示其几何意义，将数量关系和空间形式巧妙结合，来寻找解题思路，使问题得到解决.运用这一数学思想，要熟练掌握一些概念和运算的几何意义及常见曲线的代数特征.【难点磁场】1.曲线y=1+24x(–2≤x≤2)与直线y=r(x–2)+4有两个交点时，实数r的取值范围.解析：方程y=1+24x的曲线为半圆，y=r(x–2)+4为过（2，4）的直线.答案：（43,125］2.设f(x)=x2–2ax+2,当x∈［–1,+∞)时，f(x)＞a恒成立，求a的取值范围.解法一：由f(x)＞a，在［–1,+∞)上恒成立x2–2ax+2–a＞0在［–1,+∞)上恒成立.考查函数g(x)=x2–2ax+2–a的图象在［–1,+∞］时位于x轴上方.如图两种情况：(1)Δ=4a2–4(2–a)＜0a∈(–2,1)，(2)0)1(10gaa∈(–3,–2]，综上所述a∈(–3,1).解法二：由f(x)＞ax2+2＞a(2x+1)，令y1=x2+2,y2=a(2x+1),在同一坐标系中作出两个函数的图象.如图满足条件的直线l位于l1与l2之间，而直线l1、l2对应的a值（即直线的斜率）分别为1，–3，故直线l对应的a∈(–3,1).【案例探究】例1、设A={x｜–2≤x≤a}，B={y｜y=2x+3，且x∈A}，C={z｜z=x2，且x∈A}，若CB，求实数a的取值范围.命题意图：本题借助数形结合，考查有关集合关系运算的题目.知识依托：解决本题的关键是依靠一元二次函数在区间上的值域求法确定集合C.进而将CB用不等式这一数学语言加以转化.错解分析：考生在确定z=x2，x∈［–2,a］的值域是易出错，不能分类而论.巧妙观察图象将是上策.不能漏掉a＜–2这一种特殊情形.技巧与方法：解决集合问题首先看清元素究竟是什么，然后再把集合语言“翻译”为一般的数学语言，进而分析条件与结论特点，再将其转化为图形语言，利用数形结合的思想来解决.1解： y=2x+3在［–2,a］上是增函数，∴–1≤y≤2a+3，即B={y｜–1≤y≤2a+3}作出z=x2的图象，该函数定义域右端点x=a有三种不同的位置情况如下：①当–2≤a≤0时，a2≤z≤4即C={z｜z2≤z≤4}，要使CB,必须且只须2a+3≥4得a≥21与–2≤a＜0矛盾.②当0≤a≤2时，0≤z≤4即C={z｜0≤z≤4}，要使CB，由图可知：必须且只需20432aa，解得21≤a≤2③当a＞2时，0≤z≤a2，即C={z｜0≤z≤a2}，要使CB必须且只需2322aaa解得2＜a≤3④当a＜–2时，A=此时B=C=，则CB成立.综上所述，a的取值范围是(–∞,–2)∪［21,3］.例2、已知acosα+bsinα=c,acosβ+bsinβ=c(ab≠0,α–β≠kπ,k∈Z)，求证：22222cosbac.命题意图：本题主要考查数学代数式几何意义的转换能力.知识依托：解决此题的关键在于由条件式的结构联想到直线方程.进而由A、B两点坐标特点知其在单位圆上.错解分析：考生不易联想到条件式的几何意义，是为瓶颈之一.如何巧妙利用其几何意义是为瓶颈之二.技巧与方法：善于发现条件的几何意义，还要根据图形的性质分析清楚结论的几何意义，这样才能巧用数形结合方法完成解题.证明:在平面直角坐标系中，点A（cosα,sinα）与点B（cosβ,sinβ）是直线l:ax+by=c与单位圆x2+y2=1的两个交点如图.从而：｜AB｜2=(cosα–cosβ)2+(sinα–sinβ)2=2–2cos(α–β)又 单位圆的圆心到直线l的距离22||bacd由平面几何知识知｜OA｜2–(21｜AB｜)2=d2即bacd2224)cos(221∴22222cosbac.【锦囊妙计】应用数形结合的思想，应注意以下数与形的转化：（1）集合的运算及韦恩图；（2）函数及其图象；（3）数列通项及求和公式的函数特征及函数图象（4）方程（多指二元方程）及方程的曲线以形助数常用的有：借助数轴；借助函数图象；借助单位圆；借助数式的结构特征；借助于解析几何方法.以数助形常用的有：借助于几何轨迹所遵循的数量关系；借助于运算结果与几何定理的结合.【歼灭难点训练】一、选择题21.方程sin(x–4)=41x的实数解的个数是...