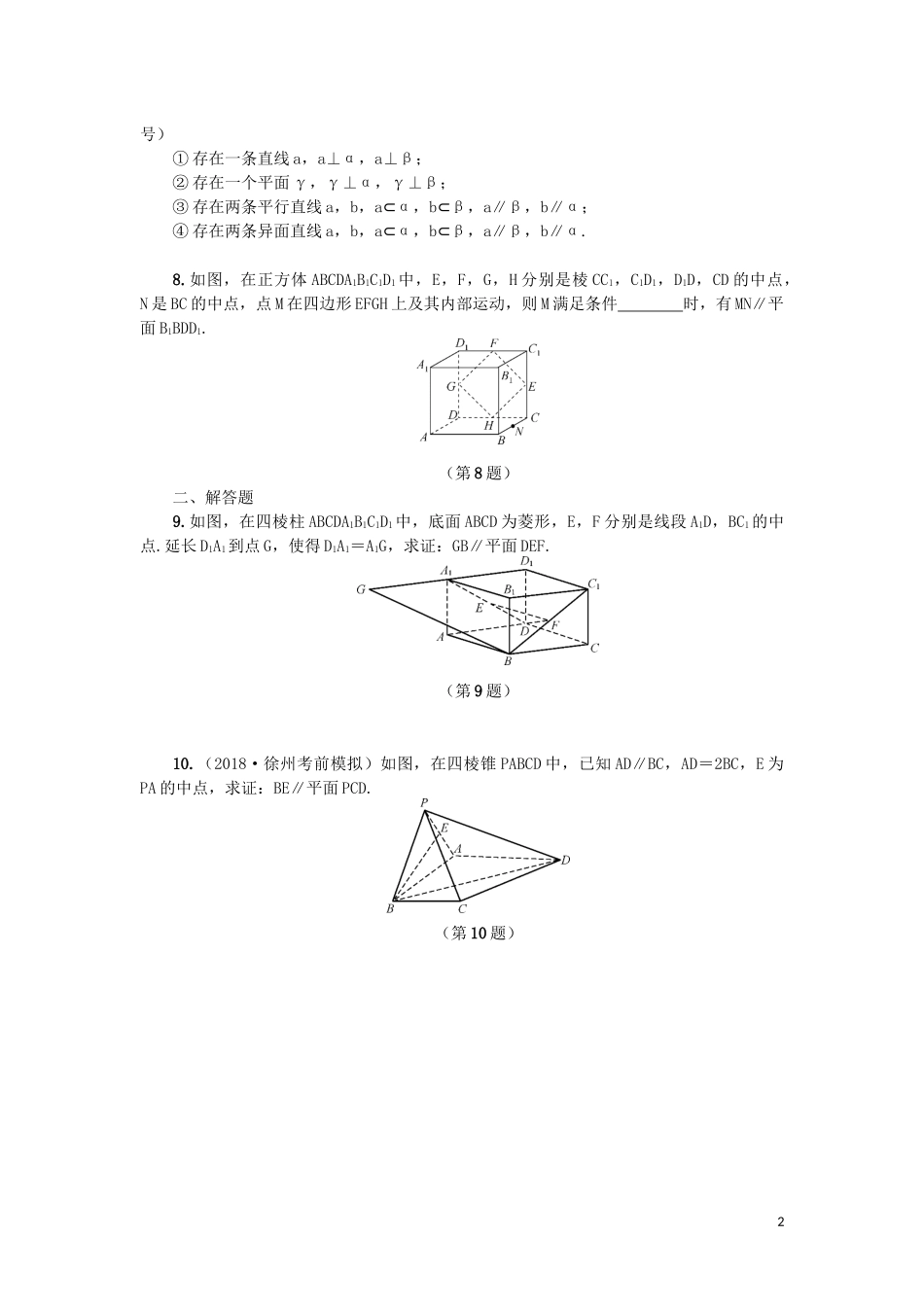
第47课直线与平面、平面与平面的平行A.课时精练一、填空题1.(2018·厦门期末)若m,n是两条不同的直线,α,β是两个不重合的平面,则下列命题中正确的是.(填序号)①若m⊂α,n⊂β,α∥β,则m∥n;②若m⊂α,α∥β,则m∥β;③若m∥α,n∥α,m⊂β,n⊂β,则α∥β;④若m∥β,m⊂α,α∩β=n,则m∥n.2.设b,c表示两条直线,α,β表示两个平面,现给出下列命题:①若b⊂α,c∥α,则b∥c;②若b⊂α,b∥c,则c∥α;③若c∥α,α⊥β,则c⊥β;④若c∥α,c⊥β,则α⊥β.其中正确的命题是.(填序号)3.已知直线m,l,n和平面α,β,给出下列命题:①若m⊂α,l∩α=A,点A∉m,则l与m不共面;②若m,l是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;③若l∥α,m∥β,α∥β,则l∥m;④若l⊂α,m⊂α,l∩m=A,l∥β,m∥β,则α∥β.其中为真命题的是.(填序号)4.已知α,β是两个平面,m,n是两条直线,给出下列命题:①若m⊥n,m⊥α,n∥β,则α⊥β;②若m⊥α,n∥α,则m⊥n;③若α∥β,m⊂α,则m∥β;④若m∥n,α∥β,则m与α所成的角和n与β所成的角相等.其中正确的命题是.(填序号)5.在下列条件中,可判定平面α与平面β平行的是.(填序号)①α,β都垂直于平面γ;②α内不共线的三个点到β的距离相等;③l,m是α内两条直线,且l∥β,m∥β;④l,m是两异面直线,且l∥α,m∥α,l∥β,m∥β.6.若l,m,n表示三条不同的直线,α,β,γ表示三个不重合的平面,给出下列命题:①若m∥n,m⊂α,n⊂β,则α∥β;②若m∥l,且m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=m,β∩γ=l,γ∩α=n,且n∥β,则l∥m.其中正确命题的个数是.7.若α,β是两个不重合的平面,则下列条件中能推出α∥β的是.(填序1号)①存在一条直线a,a⊥α,a⊥β;②存在一个平面γ,γ⊥α,γ⊥β;③存在两条平行直线a,b,a⊂α,b⊂β,a∥β,b∥α;④存在两条异面直线a,b,a⊂α,b⊂β,a∥β,b∥α.8.如图,在正方体ABCDA1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,CD的中点,N是BC的中点,点M在四边形EFGH上及其内部运动,则M满足条件时,有MN∥平面B1BDD1.(第8题)二、解答题9.如图,在四棱柱ABCDA1B1C1D1中,底面ABCD为菱形,E,F分别是线段A1D,BC1的中点.延长D1A1到点G,使得D1A1=A1G,求证:GB∥平面DEF.(第9题)10.(2018·徐州考前模拟)如图,在四棱锥PABCD中,已知AD∥BC,AD=2BC,E为PA的中点,求证:BE∥平面PCD.(第10题)211.如图,在三棱柱ABCA1B1C1中,已知AA1⊥平面ABC,AC=BC,M,N分别是棱CC1,AB的中点.(1)求证:CN⊥平面ABB1A1;(2)求证:CN∥平面AMB1.(第11题)B.滚动小练1.已知向量a,b,c在正方形网格中的位置如图所示,若c=λa+μb(λ,μ∈R),则=W.(第1题)2.已知向量a=(x,-1),b=(y,2),若a⊥b,则|a+b|的最小值是W.3.已知函数f(x)=.(1)求函数f(x)的定义域及f的值;(2)求函数f(x)在上的单调增区间.34