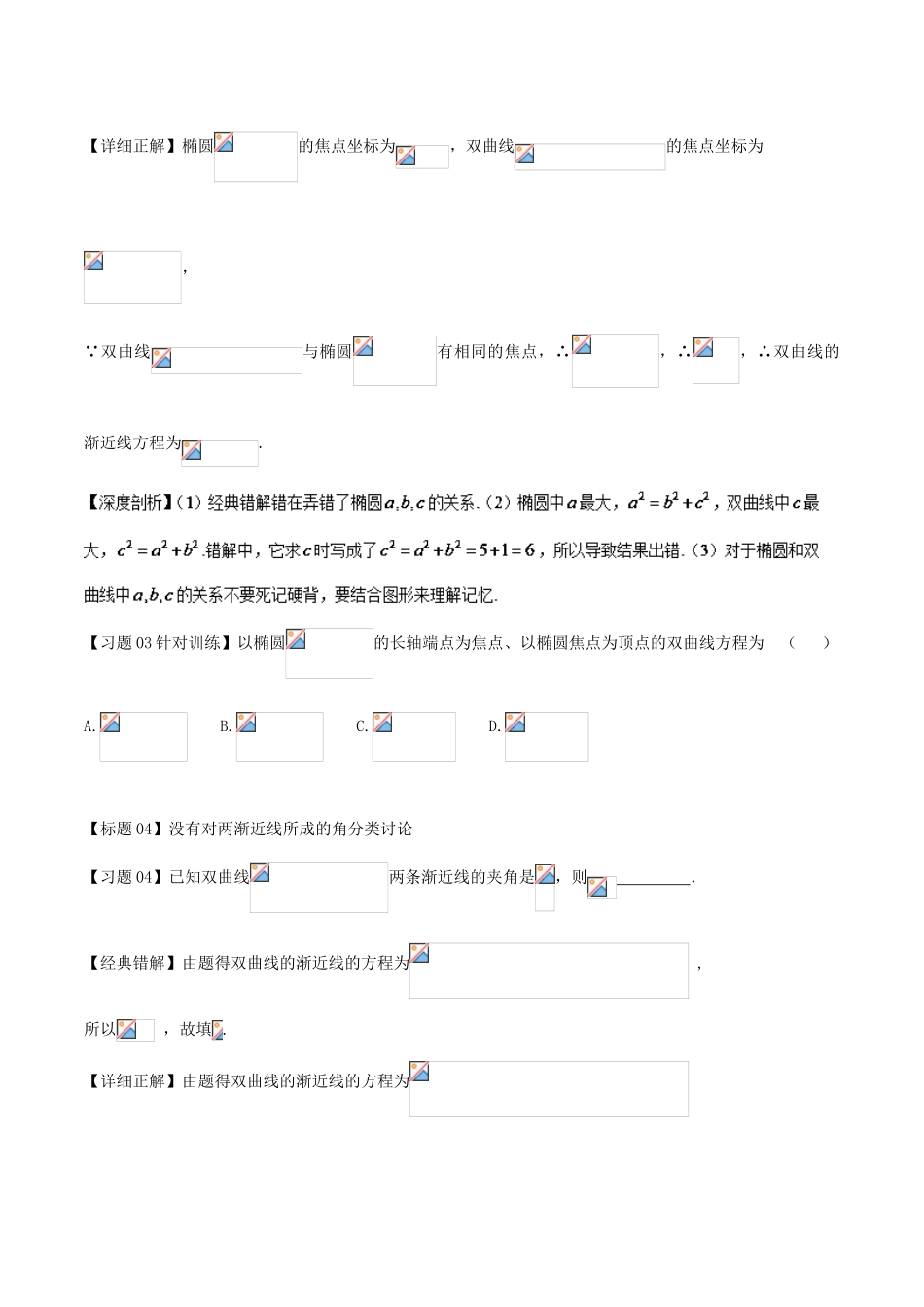
专题16圆锥曲线与方程【标题01】双曲线的定义理解片面【习题01】已知,,点满足,记点的轨迹为.求轨迹的方程.【经典错解】由可知:点的轨迹是以为焦点的双曲线,由,∴,故轨迹的方程为.【详细正解】由可知:点的轨迹是以为焦点的双曲线的右支,由,∴,故轨迹的方程为.【习题01针对训练】设,,的周长是,求的顶点的轨迹方程.【标题02】椭圆的几何性质没有过关把长轴短轴记错了【习题02】已知椭圆的对称轴是坐标轴,焦点在轴上,离心率为,长轴长为12,求椭圆的方程.【经典错解】由题得所以椭圆方程为.【详细正解】由题得所以椭圆方程为.【深度剖析】(1)经典错解错在椭圆的几何性质没有过关把长轴短轴记错了.(2)椭圆的长轴为,不是,短轴为,不是,焦距为,不是,这些基础知识不能记错.【习题02针对训练】已知焦点在轴上的椭圆的离心率为,它的长轴长等于圆的半径,则椭圆的标准方程是()A.B.C.D.【标题03】弄错了椭圆的关系【习题03】已知双曲线与椭圆有相同的焦点,则该双曲线的渐近线方程为.【经典错解】椭圆的焦点坐标为,双曲线的焦点坐标为, 双曲线与椭圆有相同的焦点,∴,∴,∴双曲线的渐近线方程为,【详细正解】椭圆的焦点坐标为,双曲线的焦点坐标为, 双曲线与椭圆有相同的焦点,∴,∴,∴双曲线的渐近线方程为.【习题03针对训练】以椭圆的长轴端点为焦点、以椭圆焦点为顶点的双曲线方程为()A.B.C.D.【标题04】没有对两渐近线所成的角分类讨论【习题04】已知双曲线两条渐近线的夹角是,则.【经典错解】由题得双曲线的渐近线的方程为,所以,故填.【详细正解】由题得双曲线的渐近线的方程为或者,所以,故填或.【习题04针对训练】已知双曲线的右焦点到其一条渐近线距离为,则实数的值是.【标题05】利用直线方程的斜截式解答时没有分类讨论【习题05】已知一条曲线在轴右边,上每一点到点的距离减去它到轴距离的差都是.(1)求曲线的方程;(2)设是过原点的直线,是与垂直相交于点,且与曲线相交于两点的直线,且,问:是否存在上述直线使成立?若存在,求出直线的方程,若不存在,请说明理由.【经典错解】(1)设是曲线上任意一点,那么点满足,化简,得.(2)设两点的坐标分别为,假设使成立的直线存在.设的方程为,由与垂直相交于点且.得,即① ∴即.将代入方程,得 与有两个交点,∴,②∴③将②代入③得化简,得. ,∴∴④由①、④得或,得存在两条直线满足条件,其方程为:或.综上,符合题意的直线有两条:或.【详细正解】(1)同上;(2)设两点的坐标分别为.假设使成立的直线存在.①当垂直于轴时,则为轴,点坐标为,,.∴,∴,不合题意.②当不垂直于轴时,设的方程为,同上略.综上,符合题意的直线有两条:或.【习题05针对训练】已知椭圆:()过点,且椭圆的离心率为.(1)求椭圆的方程;(2)若动点在直线上,过作直线交椭圆于两点,且为线段中点,再过作直线.求直线是否恒过定点,若果是则求出该定点的坐标,不是请说明理由.【标题06】把代入抛物线的方程开方时漏掉了一个解【习题06】已知抛物线上一点到焦点的距离是6,则点的坐标是.【经典错解】抛物线的焦点坐标为,设点的坐标为,由题得,所以,所以点的坐标为.【详细正解】抛物线的焦点坐标为(2,0),设点的坐标为,由题得,所以所以,所以点的坐标为.【深度剖析】(1)经典错解错在把代入抛物线的方程开方时漏掉了一个解.(2)计算时,一定要注意每一步的等价性,本题同时也可以画图观察,由对称性可知有两解.【习题06针对训练】设抛物线的焦点为,点在轴上,若线段的中点在抛物线上,且点到抛物线准线的距离为,则点的坐标为()A.(0,±2)B.(0,2)C.(0,±4)D.(0,4)【标题07】没有认真注意关键词“线段”导致出现双解【习题07】连接抛物线的焦点与点所得的线段与抛物线交于点,设点为坐标原点,则三角形的面积为()A.B.C.D.【经典错解】抛物线的焦点为且,所以直线所在的直线方程为,与抛物线方程联立有,解得,所以.故选.【详细正解】上同.解得,因为点是线段与抛物线的交点,所以点的纵坐标为,所以.故选.【习题07针对训练】已知双曲线(,)与直线有交...