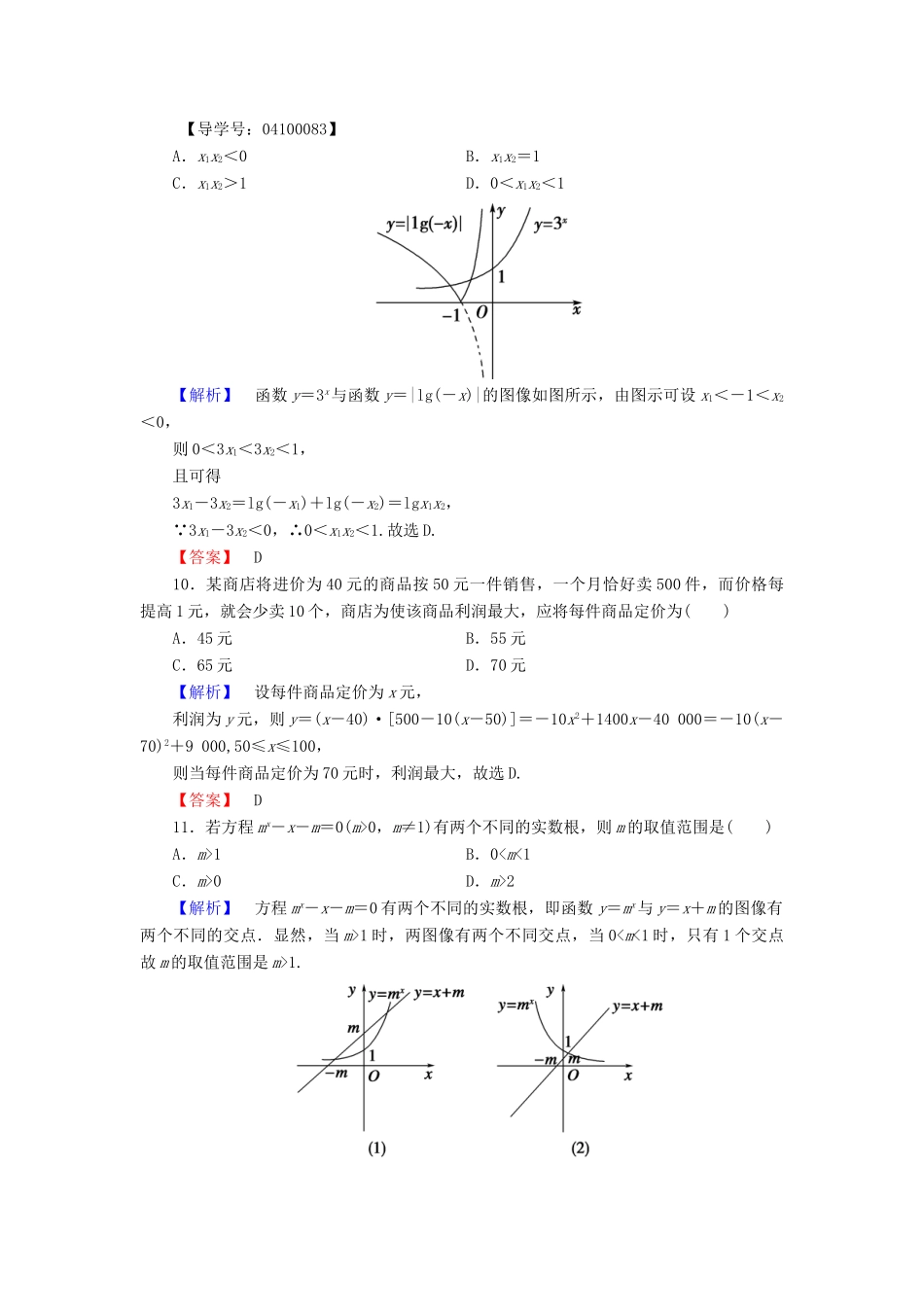
章末综合测评(四)函数应用(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数y=(x-1)(x2-2x-3)的零点为()A.1,2,3B.1,-1,3C.1,-1,-3D.无零点【解析】令y=(x-1)(x2-2x-3)=0,解得x=1,-1,3.【答案】B2.下图函数图像与x轴均有交点,其中不能用二分法求图中交点横坐标的是()【解析】由二分法的定义知应选C.【答案】C3.(2015·泉州高一检测)某同学骑车上学,离开家不久,发现作业本忘家里了,于是返回家找到作业本再上学,为了赶时间快速行驶.下图中横轴表示出发后的时间,纵轴表示离学校的距离,则较符合该同学走法的图是()【解析】该同学离学校距离先减小,后增大,再减小到0,由上述特点可知符合的是D.【答案】D4.(2015·余姚高一检测)在下列区间中,函数f(x)=ex+4x-3的零点所在的区间为()A.B.C.D.【解析】因为f=e--1-3=e--4<0,f(0)=1-3=-2<0,f=e+1-3=e-2<0,f=e+2-3=e-1>0,故零点所在区间为.【答案】C5.函数y=x2的图像与函数y=|lgx|的图像的交点个数为()A.0B.1C.2D.3【解析】在同一平面直角坐标系中分别作出y=x2和y=|lgx|的图像,如图,可得交点个数为1.【答案】B6.(2016·山东滕州市高一期中)函数f(x)=x-3+log3x的零点所在的区间是()A.(0,1)B.(1,3)C.(-∞,0)D.(3,+∞)【解析】f(1)=1-3+log31=-2<0,f(3)=3-3+log33=1>0,且f(x)在(1,3)上图像连续不断,∴f(x)零点所在的区间是(1,3),故选B.【答案】B7.某企业产值连续三年持续增长,这三年年增长率分别为P1,P2,P3,则这三年的年平均增长率为()A.(P1+P2+P3)B.C.-1D.1+(P1+P2+P3)【解析】设三年的年平均增长率为x,三年前的产值为a.则a(1+x)3=a(1+P1)(1+P2)(1+P3),则x=-1.【答案】C8.若函数f(x)=3ax+1-3a在(-1,1)上存在零点,则a的取值范围是()A.B.C.{a|a<-1}D.【解析】当a=0时,f(x)=1,无零点;当a≠0时,f(x)=3ax+1-3a为一次函数,在(-1,1)上存在零点,即f(-1)·f(1)<0,即(-3a+1-3a)(3a+1-3a)<0,解得a>.【答案】B9.设方程3x=|lg(-x)|的两个根为x1,x2,则()【导学号:04100083】A.x1x2<0B.x1x2=1C.x1x2>1D.0<x1x2<1【解析】函数y=3x与函数y=|lg(-x)|的图像如图所示,由图示可设x1<-1<x2<0,则0<3x1<3x2<1,且可得3x1-3x2=lg(-x1)+lg(-x2)=lgx1x2, 3x1-3x2<0,∴0<x1x2<1.故选D.【答案】D10.某商店将进价为40元的商品按50元一件销售,一个月恰好卖500件,而价格每提高1元,就会少卖10个,商店为使该商品利润最大,应将每件商品定价为()A.45元B.55元C.65元D.70元【解析】设每件商品定价为x元,利润为y元,则y=(x-40)·[500-10(x-50)]=-10x2+1400x-40000=-10(x-70)2+9000,50≤x≤100,则当每件商品定价为70元时,利润最大,故选D.【答案】D11.若方程mx-x-m=0(m>0,m≠1)有两个不同的实数根,则m的取值范围是()A.m>1B.00D.m>2【解析】方程mx-x-m=0有两个不同的实数根,即函数y=mx与y=x+m的图像有两个不同的交点.显然,当m>1时,两图像有两个不同交点,当01.【答案】A12.某商店计划投入资金20万元经销甲或乙两种商品,已知经销甲商品与乙商品所获得的利润分别为P(万元)和Q(万元),且它们与投入资金x(万元)的关系是:P=,Q=·(a>0).若不管资金如何投放,经销这两种商品或其中的一种商品所获得的纯利润总不少于5万元,则a的最小值应为()A.B.5C.±D.-【解析】设投放x万元经销甲商品,则投放(20-x)万元经销乙商品,总利润y=P+Q=+·.令y≥5,则+·≥5,a≥10-,即a≥对0≤x<20恒成立.而f(x)=的最大值为,且x=20时,a≥10-也成立,amin=,故选A.【答案】A二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.函数y=x2与函数y=xlnx在区间(0,+∞)上增长较快的一个是________.【解析】因为y=lnx的增长越来越慢.y=xlnx增长与y=x2相比会越来越慢,...