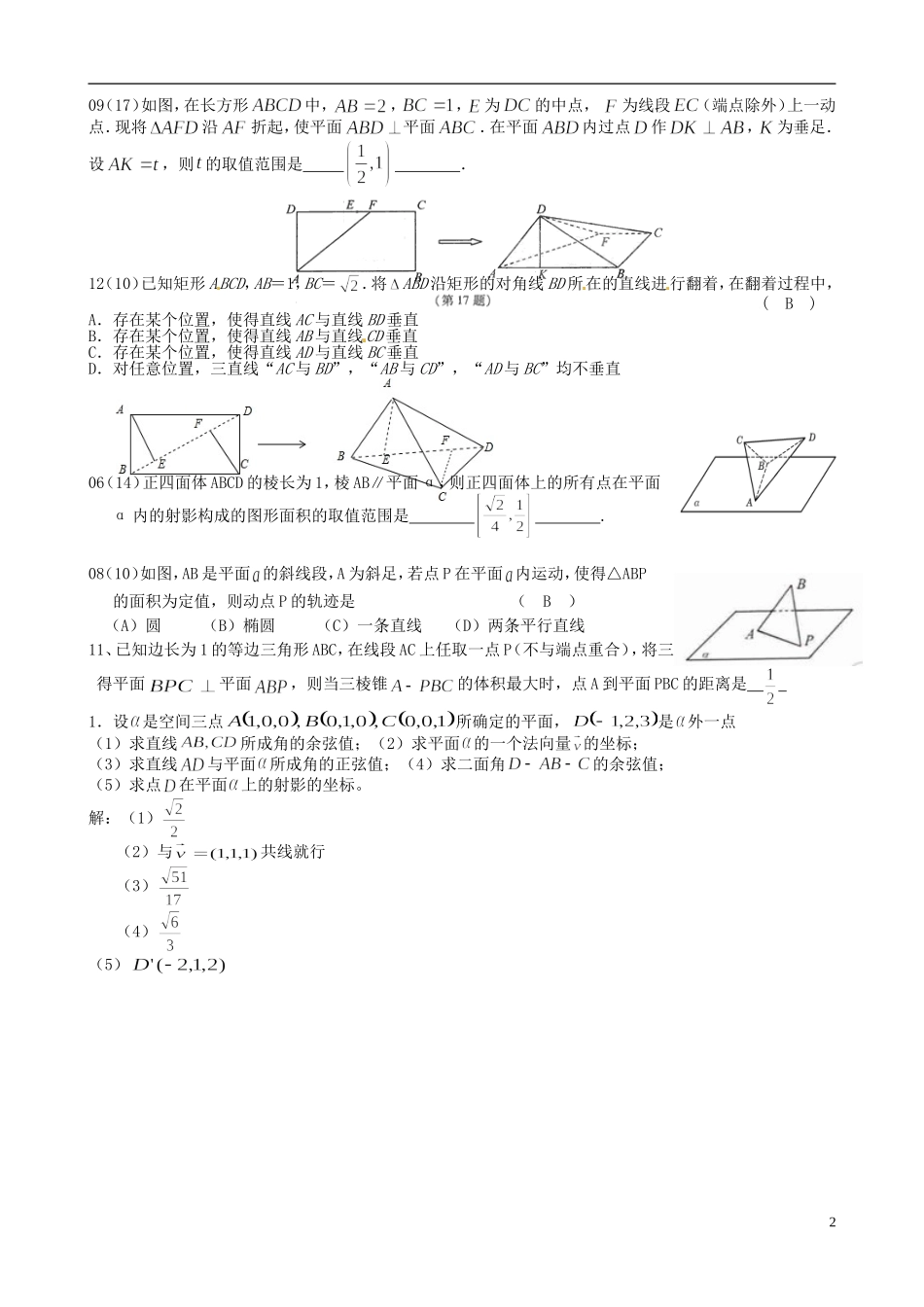
AB高一立体几何综合练习(1)参考答案04(10)如图,在正三棱柱ABC—A1B1C1中已知AB=1,D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则α=(D)(A)(B)(C)(D)09(5)在三棱柱中,各棱长相等,侧棱垂直于底面,点是侧面的中心,则与平面所成角的大小是(C)A.B.C.D.04(16)已知平面和平面交于直线,P是空间一点,PA⊥,垂足为A,PB⊥,垂足为B,且PA=1,PB=2,若点A在内的射影与点B在内的射影重合,则点P到的距离为.1.如图,四棱锥S—ABCD的底面为正方形,SD底面ABCD,则下列结论中不正确的是(D)A.AC⊥SBB.AB∥平面SCDC.SA与平面SBD所成的角等于SC与平面SBD所成的角D.AB与SC所成的角等于DC与SA所成的角2.正方体ABCD-中,B1B与平面AC所成角的余弦值为(D)A23BC23D3.在长方体ABCD-A1B1C1D1中,AA1=AD=2AB.若E,F分别为线段A1D1,CC1的中点,则直线EF与平面ABB1A1所成角的余弦值为(A)(A)(B)(C)(D)5.如图,在空间直角坐标系中有直三棱柱,,则直线与直线夹角的余弦值为(B)A.B.C.D.6.如图,二面角的大小是60°,线段.,与所成的角为30°.则与平面所成的角的正弦值是.7.已知二面角α-l-β为60o,动点P、Q分别在面α、β内,P到β的距离为3,Q到α的距离为23,则P、Q两点之间距离的最小值为;8.在三棱锥S-ABC中,△ABC为正三角形,且A在面SBC上的射影H是△SBC的垂心,又二面角H-AB-C为300,则;05(12).设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于____90°_____.1ABCDEMN09(17)如图,在长方形中,,,为的中点,为线段(端点除外)上一动点.现将沿折起,使平面平面.在平面内过点作,为垂足.设,则的取值范围是.12(10)已知矩形ABCD,AB=1,BC=.将ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,(B)A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直06(14)正四面体ABCD的棱长为1,棱AB∥平面α,则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是.08(10)如图,AB是平面的斜线段,A为斜足,若点P在平面内运动,使得△ABP的面积为定值,则动点P的轨迹是(B)(A)圆(B)椭圆(C)一条直线(D)两条平行直线11、已知边长为1的等边三角形ABC,在线段AC上任取一点P(不与端点重合),将三角形ABP沿BP折起,使得平面平面,则当三棱锥的体积最大时,点A到平面PBC的距离是1.设是空间三点所确定的平面,是外一点(1)求直线所成角的余弦值;(2)求平面的一个法向量的坐标;(3)求直线与平面所成角的正弦值;(4)求二面角的余弦值;(5)求点在平面上的射影的坐标。解:(1)(2)与共线就行(3)(4)(5)2