（江苏专用）高考数学大一轮复习 第四章 第24课 两角和与差的三角函数自主学习-人教版高三全册数学试题VIP免费

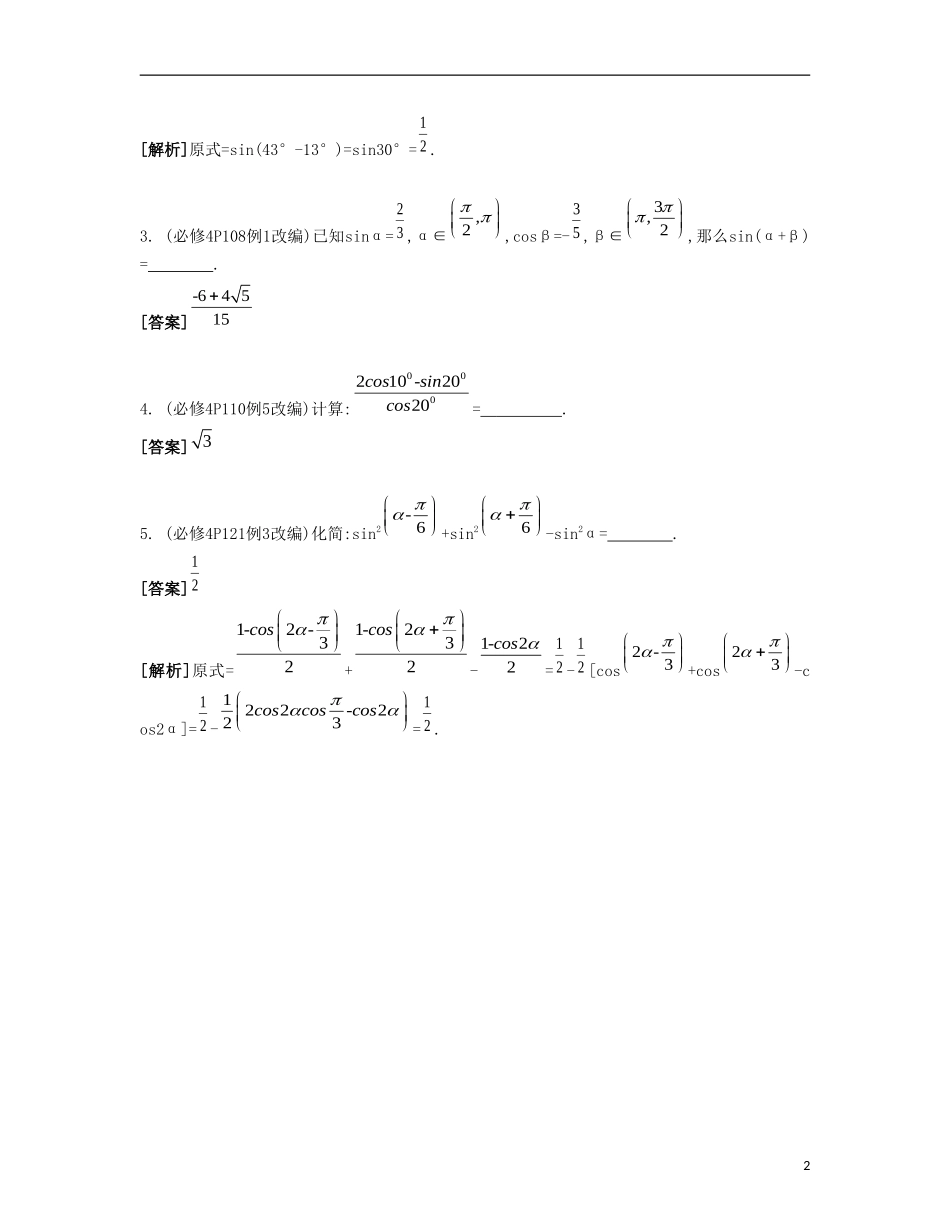
第24课两角和与差的三角函数(本课对应学生用书第50-51页)自主学习回归教材1.两角和(差)的三角函数公式(1)sin(α±β)=sinαcosβ±cosαsinβ;(2)cos(α±β)=cosαcosβ∓sinαsinβ;(3)tan(α±β)=1tantantantan.2.注意两角和(差)的三角函数公式的变形运用asinx+bcosx=222222,,c.bsinababaosabsinxφφ其中满足3.注意几种常见的角的变换(1)α=(α+β)-β=(α-β)+β;(2)2α=(α+β)+(α-β);(3)2α+β=α+(α+β).1.(必修4P115练习1改编)已知tanα=4,tanβ=3,那么tan(α+β)=.[答案]-711[解析]由题意得tan(α+β)=1-·tantantantan=431-12=-711.2.(必修4P96练习4改编)计算:sin43°cos13°-sin13°cos43°=.[答案]121[解析]原式=sin(43°-13°)=sin30°=12.3.(必修4P108例1改编)已知sinα=23,α∈,2,cosβ=-35,β∈3,2,那么sin(α+β)=.[答案]-645154.(必修4P110例5改编)计算:000210-2020cossincos=.[答案]35.(必修4P121例3改编)化简:sin2-6+sin26-sin2α=.[答案]12[解析]原式=1-2-32cos+1-232cos-1-22cos=12-12[cos2-3+cos23-cos2α]=12-122-223coscoscos=12.2