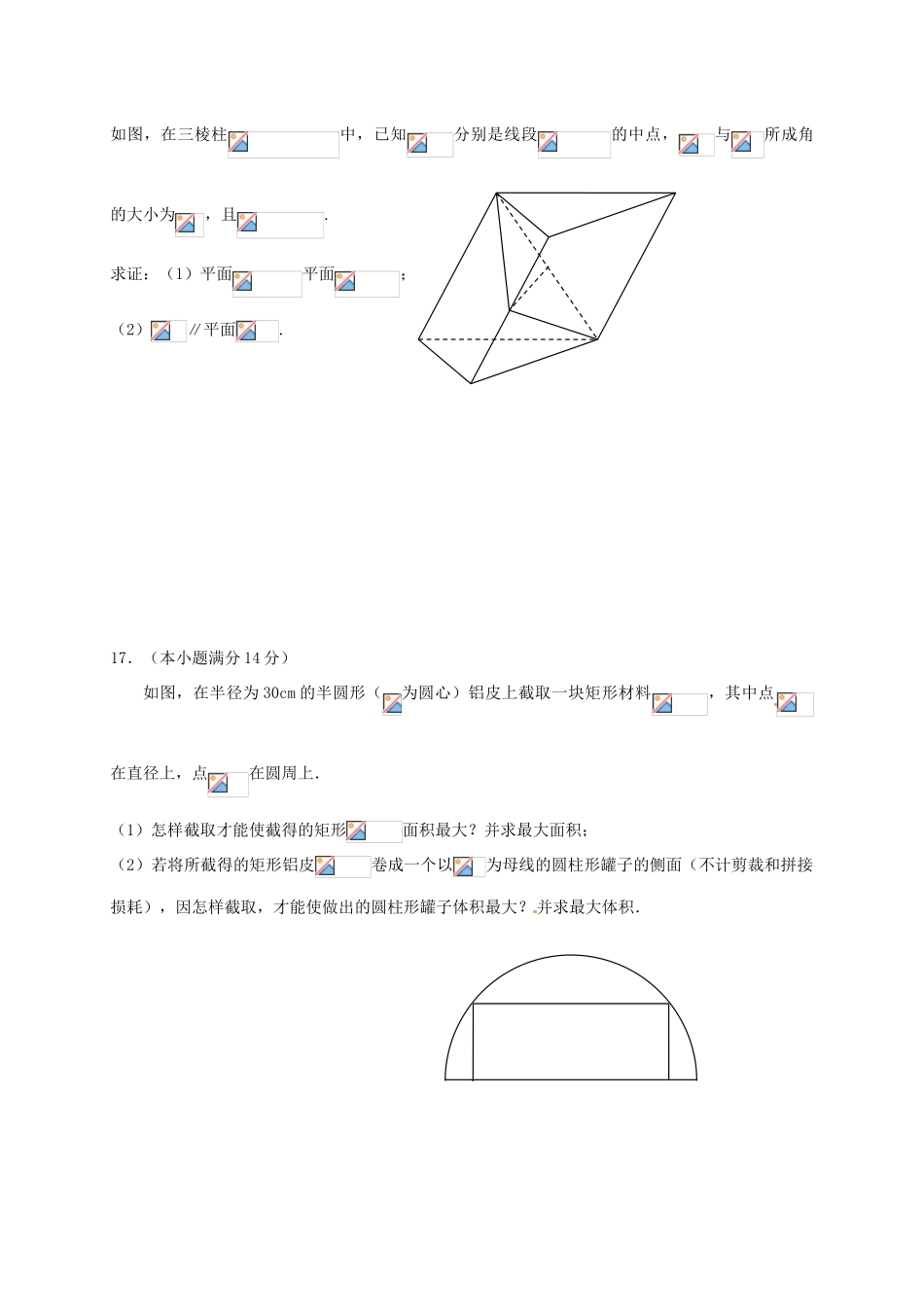
2017届高三年级第二学期周考(9)数学试题(总分160分,考试时间120分钟)一、填空题:(本大题共14个小题,每小题5分,共70分,将答案填在答题纸上)1.已知集合,集合,则集合等于___▲____.2.已知是虚数单位,则复数的虚部为____▲____.3.已知函数在处的导数为,则实数的值为____▲____.4.阅读算法流程图,运行相应的程序,输出的结果为▲.5.一种水稻试验品种连续5年的平均单位面积产量(单位:t/hm2)如下:9.8,9.9,10.1,10,10.2,则该组数据的方差为▲.6.袋中有形状大小都相同的5只球,其中1只白球,2只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为___▲___.7.已知抛物线的焦点为,准线为,过抛物线上一点作于,若直线的斜率为,则▲.8.在等比数列中,若,则的值为▲.9.已知平面上三点的坐标为,其中,若,则的值为▲.N(第6题图)开始z←x+yx←1,y←1z<6y←zY输出结束x←y10.定义在上的函数满足,则的值为▲.11.已知实数满足,若不等式恒成立,则实数的最小值为▲.12.已知圆,圆,若圆上存在点,过点作圆的两条切线,切点为,使得,则实数的取值范围是▲.13.已知是定义在上的单调函数,且对任意,都有成立,则函数的值域为▲.14.在中,角所对应的边分别为,其中,则的最小值为▲.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.(本小题满分14分)已知,.(1)求的值;(2)求的值.16.(本小题满分14分)如图,在三棱柱中,已知分别是线段的中点,与所成角的大小为,且.求证:(1)平面平面;(2)∥平面.17.(本小题满分14分)如图,在半径为30cm的半圆形(为圆心)铝皮上截取一块矩形材料,其中点在直径上,点在圆周上.(1)怎样截取才能使截得的矩形面积最大?并求最大面积;(2)若将所截得的矩形铝皮卷成一个以为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),因怎样截取,才能使做出的圆柱形罐子体积最大?并求最大体积.18.(本小题满分16分)已知椭圆的左、右焦点分别为,离心率为,直线与椭圆的两个交点间的距离为.(1)求椭圆的方程;(2)分别过作,满足,设与的上半部分分别交于两点,求四边形面积的最大值.19.(本小题满分16分)已知,,为的导函数.(1)求的零点;(2)求的值域;(3)若在定义域上存在,使得,求证:.20.(本小题满分16分)已知各项均为正数的数列的前项和为,数列的前项和为,满足,.(1)求的值及数列的通项公式;(2)是否存在,使得成为一直角三角形的三边?若存在指出的关系,若不存在,请说明理由;(3)若数列的通项公式为,数列满足,中不存在这样的项,同时成立(其中)试求实数的取值范围.