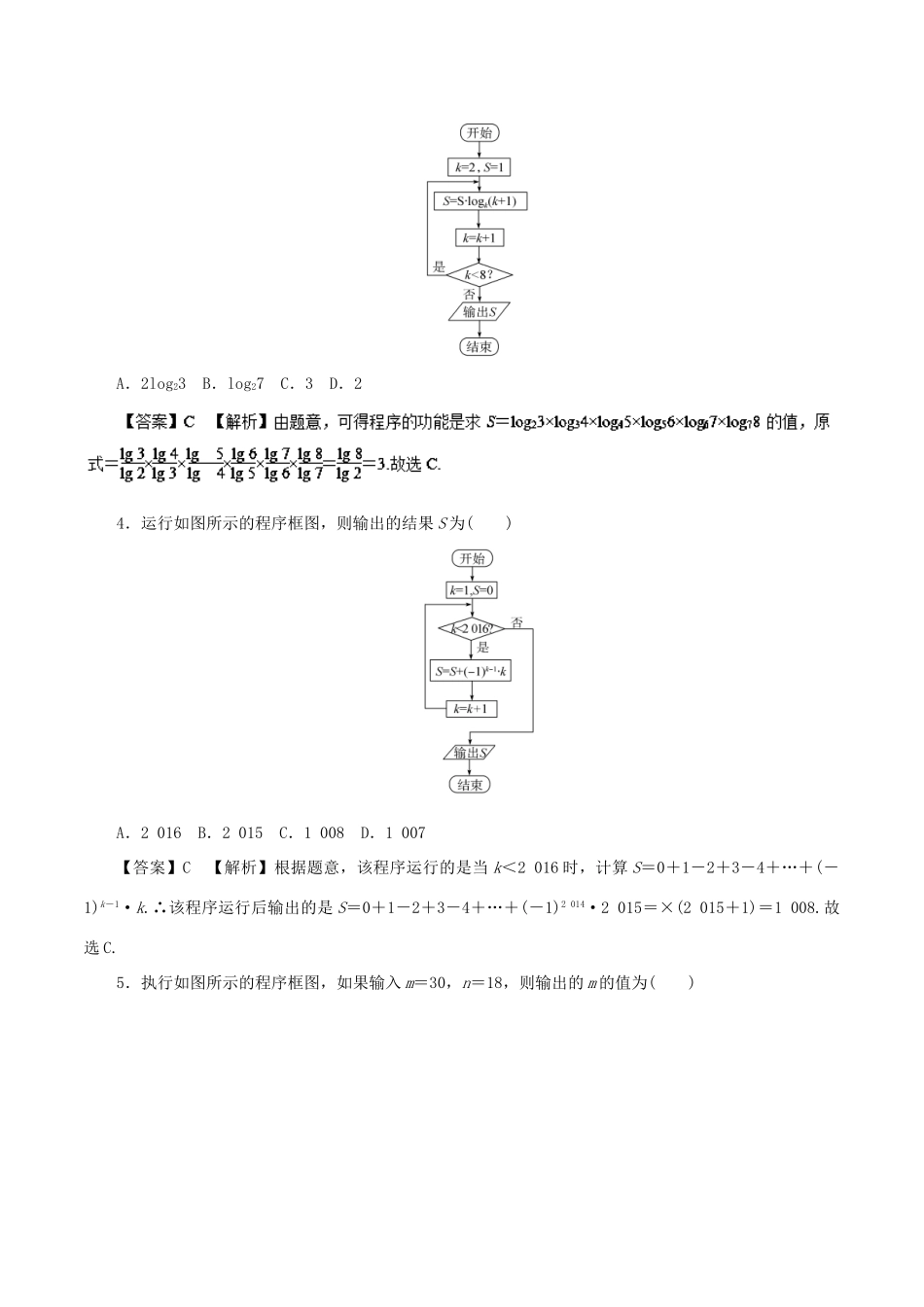
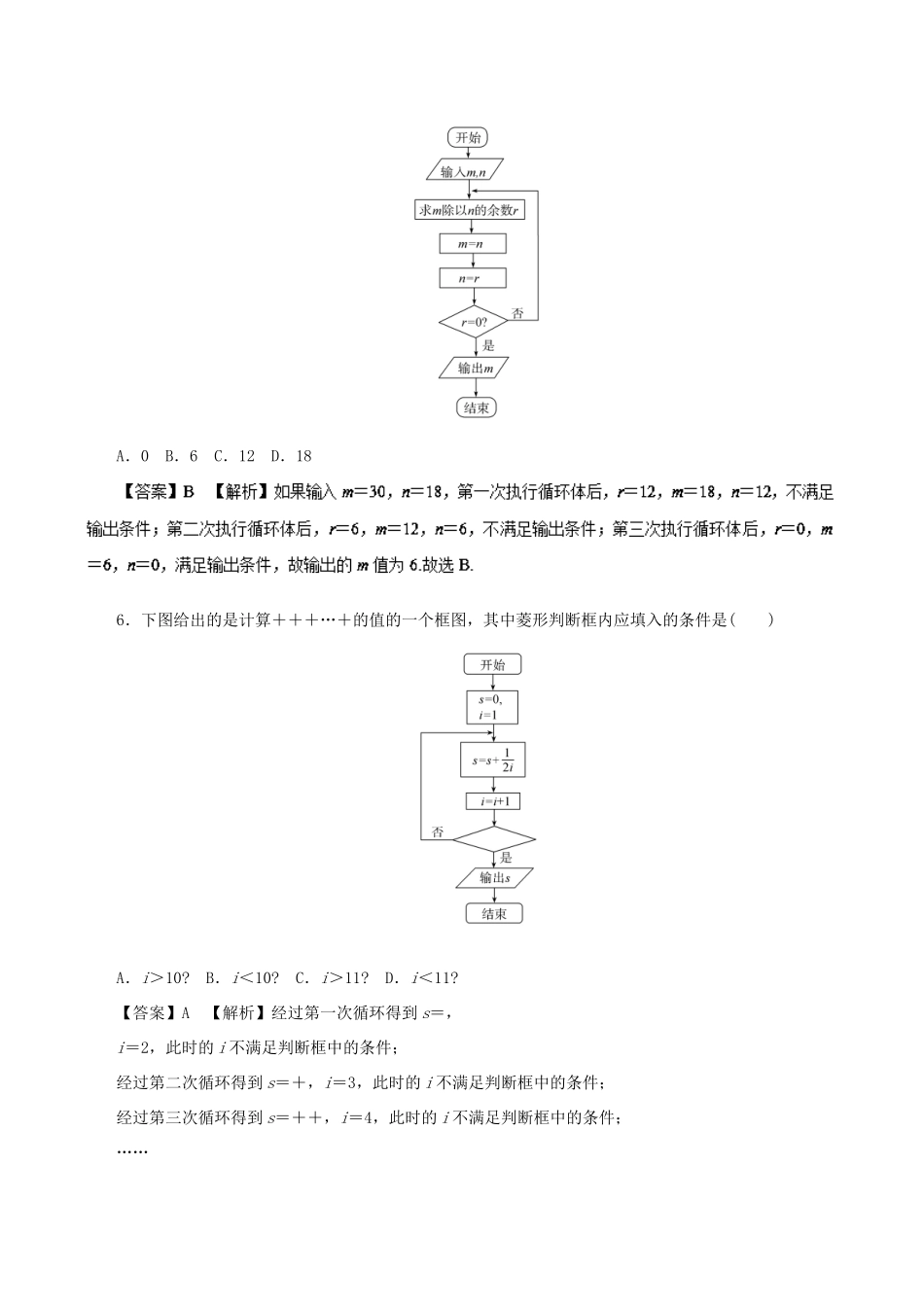
专题18算法、复数、推理与证明1.如图所示程序框图(算法流程图)的输出结果是()A.3B.11C.38D.123【答案】D【解析】第一步:a=12+2=3<12,第二步:a=32+2=11<12,第三步:a=112+2=123>12,跳出循环,输出a=123.故选D.2.执行如图所示的程序框图,若输出的S=88,则判断框内应填入的条件是()A.k>4?B.k>5?C.k>6?D.k>7?3.若执行如图所示的程序框图,输出S的值为()A.2log23B.log27C.3D.24.运行如图所示的程序框图,则输出的结果S为()A.2016B.2015C.1008D.1007【答案】C【解析】根据题意,该程序运行的是当k<2016时,计算S=0+1-2+3-4+…+(-1)k-1·k.∴该程序运行后输出的是S=0+1-2+3-4+…+(-1)2014·2015=×(2015+1)=1008.故选C.5.执行如图所示的程序框图,如果输入m=30,n=18,则输出的m的值为()A.0B.6C.12D.186.下图给出的是计算+++…+的值的一个框图,其中菱形判断框内应填入的条件是()A.i>10?B.i<10?C.i>11?D.i<11?【答案】A【解析】经过第一次循环得到s=,i=2,此时的i不满足判断框中的条件;经过第二次循环得到s=+,i=3,此时的i不满足判断框中的条件;经过第三次循环得到s=++,i=4,此时的i不满足判断框中的条件;……经过第十次循环得到s=+++…+,i=11,此时的i满足判断框中的条件,执行输出,故判断框中的条件是i>10?.故选A.7.如图所示的程序框图所表示的算法的功能是()A.计算1+++…+的值B.计算1+++…+的值C.计算1+++…+的值D.计算1+++…+的值8.已知z=1+i,则(z)2=()A.2B.-2C.2iD.-2i【答案】D【解析】 z=1+i,∴z=1-i,(z)2=-2i,故选D.9.已知复数是纯虚数,则实数a=()A.-2B.4C.-6D.6【答案】D【解析】=, 复数为纯虚数,∴a=6.10.如图,在复平面内,复数z1,z2对应的向量分别是OA,OB,则|z1+z2|=()A.2B.3C.2D.3【答案】A【解析】由题图可知,z1=-2-i,z2=i,则z1+z2=-2,∴|z1+z2|=2,故选A.11.在复平面内,复数z和表示的点关于虚轴对称,则复数z=()A.+iB.-iC.-+iD.--i12.如果复数(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于()A.B.C.-D.2【答案】C【解析】==-i.由=,得b=-.13.设i是虚数单位,z是复数z的共轭复数.若z·zi+2=2z,则z=()A.1+iB.1-iC.-1+iD.-1-i【答案】A【解析】令z=a+bi,则z=a-bi,代入z·zi+2=2z,得:(a2+b2)i+2=2a+2bi,得a2+b2=2b且2a=2,解得a=1,b=1,则z=1+i,故选A.14.在复平面内,复数3-4i,i(2+i)对应的点分别是A,B,则线段AB的中点C对应的复数为()A.-2+2iB.2-2iC.-1+iD.1-i【答案】D【解析】 i(2+i)=-1+2i,∴复数3-4i,i(2+i)对应的点A,B的坐标分别为A(3,-4),B(-1,2).∴线段AB的中点C的坐标为(1,-1),则线段AB的中点C对应的复数为1-i.故选D.15.设a>0,f(x)=,令a1=1,an+1=f(an),n∈N*.(1)写出a2,a3,a4的值,并猜想数列{an}的通项公式;(2)用数学归纳法证明你的结论.16.各项都为正数的数列{an}满足a1=1,a-a=2.(1)求数列{an}的通项公式;(2)求证:++…+≤对一切n∈N*恒成立.【解析】(1)因为a-a=2,所以数列{a}是首项为1,公差为2的等差数列,所以a=1+(n-1)·2=2n-1,又an>0,则an=.(2)证明:由(1)知,即证1++…+≤.①当n=1时,左边=1,右边=1,所以不等式成立;当n=2时,左边<右边,所以不等式成立.②假设当n=k(k≥2,k∈N*)时不等式成立,即1++…+≤,当n=k+1时,左边=1++…++≤+<+=+==.所以当n=k+1时不等式成立.由①②知对一切n∈N*不等式恒成立.17.已知函数f(x)=x2-ax+ln(x+1)(a∈R).(1)当a=2时,求函数f(x)的极值点;(2)若函数f(x)在区间(0,1)上恒有f′(x)>x,求实数a的取值范围;(3)已知a<1,c1>0,且cn+1=f′(cn)(n=1,2,…),证明数列{cn}是单调递增数列.(2)因为f′(x)=2x-a+,由f′(x)>x,得2x-a+>x,所以由题意知,a<x+(0<x<1)恒成立.又x+=x+1+-1≥1,当且仅当x...