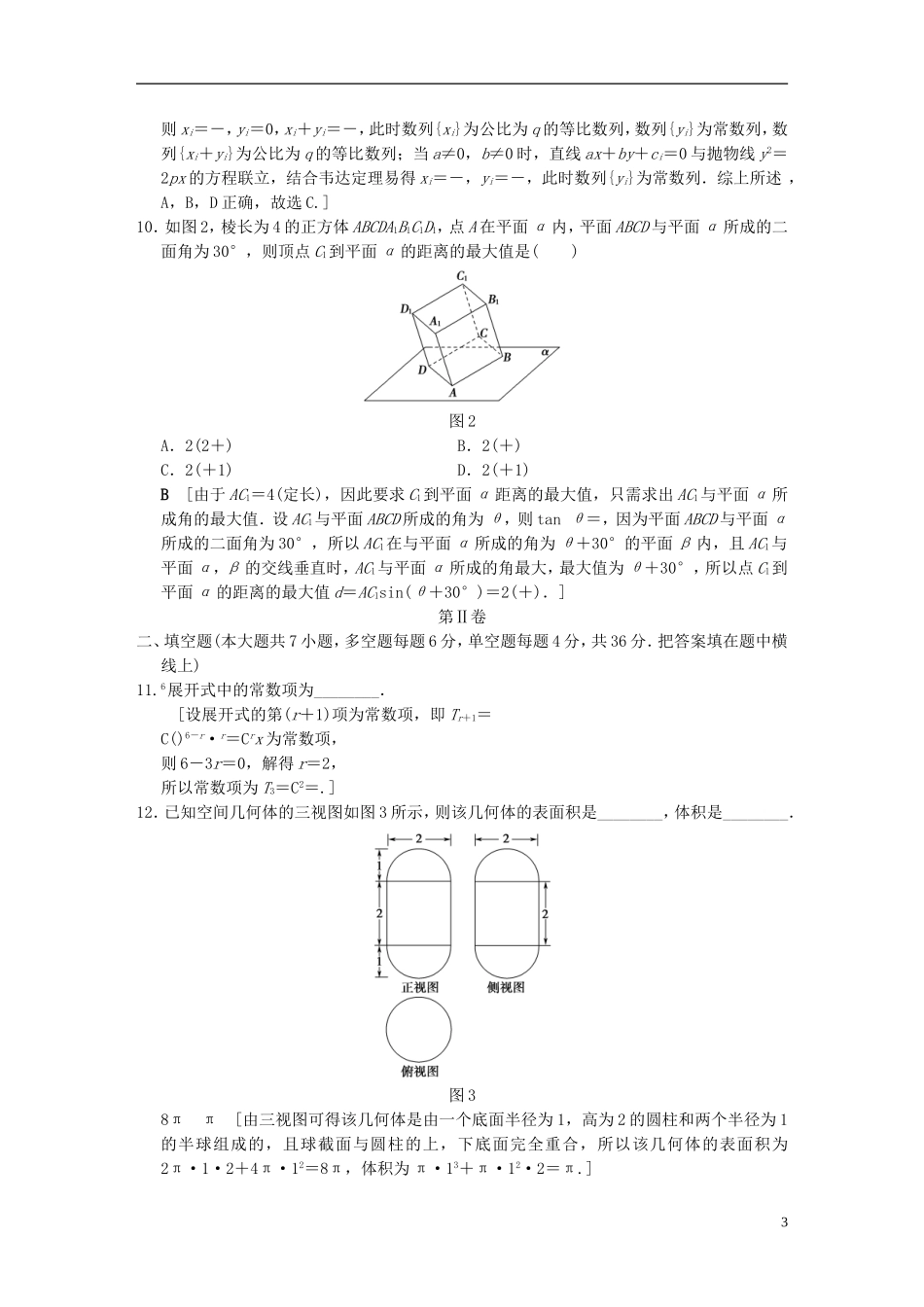
2018年浙江高考仿真卷(三)(对应学生用书第171页)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.定义集合A={x|f(x)=},B={y|y=log2(2x+2)},则A∩∁RB=()A.(1,+∞)B.[0,1]C.[0,1)D.[0,2)B[由2x-1≥0得x≥0,即A=[0,+∞),由于2x>0,所以2x+2>2,所以log2(2x+2)>1,即B=(1,+∞),所以A∩∁RB=[0,1],故选B.]2.△ABC的三个内角A,B,C的对边分别是a,b,c,则“a2+b2-,故D错误.]5.设函数f(x)=若函数g(x)=f(x)-m在[0,2π]内恰有4个不同的零点,则实数m的取值1范围是()A.(0,1)B.[1,2]C.(0,1]D.(1,2)A[函数g(x)=f(x)-m在[0,2π]内有4个不同的零点,即曲线y=f(x)与直线y=m在[0,2π]上有4个不同的交点,画出图象如图所示,结合图象可得出00,b>0)的左,右焦点,以F1F2为直径的圆与双曲线在第一象限的交点为P,过点P向x轴作垂线,垂足为H,若|PH|=a,则双曲线的离心率为()A.B.C.D.C[由题意可得点P的坐标为(b,a),又P在双曲线上,故有-=1,即=,所以b2=ac,即c2-ac-a2=0,所以e2-e-1=0,解得e=(负值舍去).]7.已知3tan+tan2=1,sinβ=3sin(2α+β),则tan(α+β)=()A.B.-C.-D.-3B[由3tan+tan2=1得=,所以tanα=.①由sinβ=3sin(2α+β)得sin[(α+β)-α]=3sin[(α+β)+α],展开并整理得,2sin(α+β)cosα=-4cos(α+β)sinα,所以tan(α+β)=-2tanα,②由①②得tan(α+β)=-.]8.已知f(x)=2x2-4x-1,设有n个不同的数xi(i=1,2,…,n)满足0≤x10)均相交,所成弦的中点为Mi(xi,yi),则下列说法错误的是()A.数列{xi}可能是等比数列B.数列{yi}是常数列C.数列{xi}可能是等差数列D.数列{xi+yi}可能是等比数列C[设等比数列{ci}的公比为q.当a=0,b≠0时,直线by+ci=0与抛物线y2=2px最多有一个交点,不符合题意;当a≠0,b=0时,直线ax+ci=0与抛物线y2=2px的交点为,2则xi=-,yi=0,xi+yi=-,此时数列{xi}为公比为q的等比数列,数列{yi}为常数列,数列{xi+yi}为公比为q的等比数列;当a≠0,b≠0时,直线ax+by+ci=0与抛物线y2=2px的方程联立,结合韦达定理易...