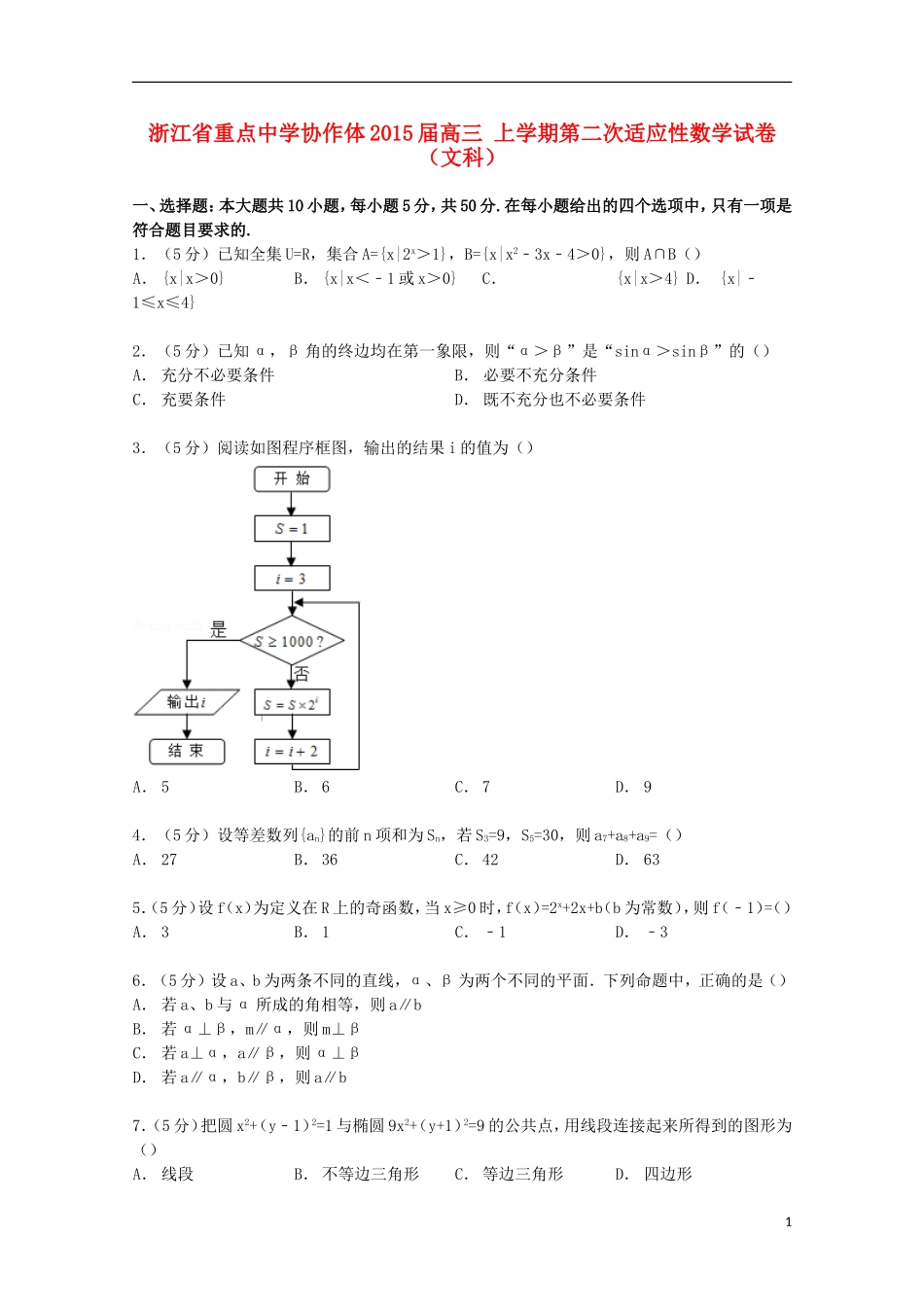
浙江省重点中学协作体2015届高三上学期第二次适应性数学试卷(文科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知全集U=R,集合A={x|2x>1},B={x|x2﹣3x﹣4>0},则A∩B()A.{x|x>0}B.{x|x<﹣1或x>0}C.{x|x>4}D.{x|﹣1≤x≤4}2.(5分)已知α,β角的终边均在第一象限,则“α>β”是“sinα>sinβ”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(5分)阅读如图程序框图,输出的结果i的值为()A.5B.6C.7D.94.(5分)设等差数列{an}的前n项和为Sn,若S3=9,S5=30,则a7+a8+a9=()A.27B.36C.42D.635.(5分)设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(﹣1)=()A.3B.1C.﹣1D.﹣36.(5分)设a、b为两条不同的直线,α、β为两个不同的平面.下列命题中,正确的是()A.若a、b与α所成的角相等,则a∥bB.若α⊥β,m∥α,则m⊥βC.若a⊥α,a∥β,则α⊥βD.若a∥α,b∥β,则a∥b7.(5分)把圆x2+(y﹣1)2=1与椭圆9x2+(y+1)2=9的公共点,用线段连接起来所得到的图形为()A.线段B.不等边三角形C.等边三角形D.四边形18.(5分)设f(x)=|lnx|,若函数g(x)=f(x)﹣ax在区间(0,3]上有三个零点,则实数a的取值范围是()A.(0,)B.(,e)C.(0,]D.[,)9.(5分)各项为实数的等差数列的公差为4,其首项的平方与其余各项之和不超过100,这样的数列至多有()项.A.5B.6C.7D.810.(5分)在等腰三角形ABC中,AB=AC,D在线段AC,AD=kAC(k为常数,且0<k<1),BD=l为定长,则△ABC的面积最大值为()A.B.C.D.二、填空题:本大题共7小题,每小题4分,共28分.11.(4分)若某棱锥的三视图(单位:cm)如图所示,则该棱锥的体积等于cm312.(4分)设x0是方程10﹣x=lnx的解,且x0∈(k,k+1)(k∈Z,则k=.13.(4分)已知函数f(x)=在R上是单调函数,则实数a的取值范围是.14.(4分)在△ABC中,若sinA=2cosBcosC,则tanB+tanC=.15.(4分)若实数x,y满足且z=2x+y的最小值为3,则实数b的值为.216.(4分)已知△ABC中,•=•,|+|=2,且B∈[,],则的取值范围是.17.(4分)已知双曲线的左右焦点为F1,F2,P为右支上的任一点,若的最小值为8a,则离心率的取值范围是.三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.18.(14分)已知,(Ⅰ)求tanx的值;(Ⅱ)求的值.19.(14分)在△ABC中,角A,B,C所对的边分别为a,b,c,角B为锐角,且sinB=(1)求sin2+cos2B的值;(2)若b=2,求ac的最大值.20.(15分)已知数列{an}的前n项和Sn满足:Sn=t(Sn﹣an+1)(t为常数,且t≠0,t≠1).(1)求{an}的通项公式;(2)设bn=an2+Sn﹣an,若数列{bn}为等比数列,求t的值;(3)在满足条件(2)的情形下,设cn=4an+1,数列{cn}的前n项和为Tn,若不等式≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.21.(15分)在直三棱柱ABC﹣A′B′C′中,底面ABC是边长为2的正三角形,D′是棱A′C′的中点,且AA′=2.(Ⅰ)试在棱CC′上确定一点M,使A′M⊥平面AB′D′;(Ⅱ)当点M在棱CC′中点时,求直线AB′与平面A′BM所成角的大小.322.(14分)已知动圆∴a2+c2﹣b2=ac,b=2过定点M(0,2),且在x轴上截得弦长为4.设该动圆圆心的轨迹为曲线C(1)求曲线C方程;(2)点A为直线l:x﹣y﹣2=0上任意一点,过A作曲线C的切线,切点分别为P、Q,△APQ面积的最小值及此时点A的坐标.浙江省重点中学协作体2015届高三上学期第二次适应性数学试卷(文科)参考答案与试题解析一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知全集U=R,集合A={x|2x>1},B={x|x2﹣3x﹣4>0},则A∩B()A.{x|x>0}B.{x|x<﹣1或x>0}C.{x|x>4}D.{x|﹣1≤x≤4}考点:交集及其运算.专题:不等式的解法及应用.分析:集合A和集合B的公共元素构成集合A∩B,由此利用集合A={x|2x>1},B={x|x2﹣3x...