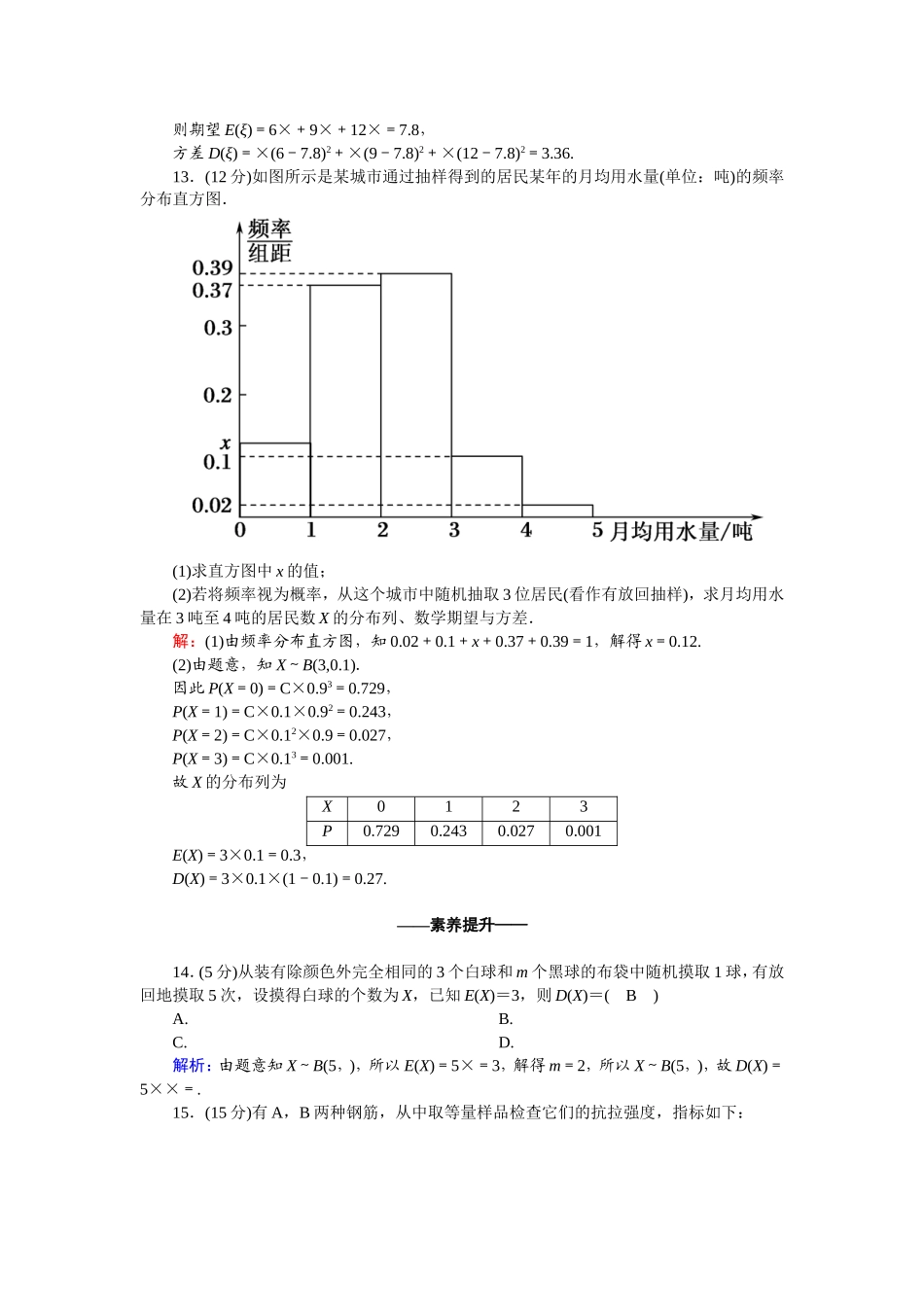
课时作业15离散型随机变量的方差时间:45分钟分值:100分一、选择题(每小题5分,共计40分)1.已知随机变量ξ的分布列为:ξ-101P则在下列式子①E(ξ)=-,②D(ξ)=,③P(ξ=0)=中,正确的有(C)A.0个B.1个C.2个D.3个解析:由分布列可知P(ξ=0)=,根据公式可求得E(ξ)=-,D(ξ)=,所以①③正确.2.随机变量X服从二项分布X~B(100,0.2),那么D(4X+3)的值为(B)A.64B.256C.259D.320解析:由题意知,D(X)=100×0.2×(1-0.2)=16,所以,D(4X+3)=42×D(X)=16×16=256.3.已知X是离散型随机变量,P(X=1)=,P(X=a)=,E(X)=,则D(2X-1)=(D)A.B.-C.D.解析:由题意,知1×+a×=,解得a=2,∴D(X)=(1-)2×+(2-)2×=,∴D(2X-1)=22D(X)=4×=.4.设10≤x1D(X2)B.D(X1)=D(X2)C.D(X1)D(X2).5.已知随机变量ξ+η=8,若ξ~B(10,0.4),则E(η)和D(η)分别是(B)A.2和2.4B.4和2.4C.6和2.4D.4和5.6解析:因为ξ~B(10,0.4),所以E(ξ)=10×0.4=4,D(ξ)=10×0.4×(1-0.4)=2.4.又ξ+η=8,所以η=8-ξ,所以E(η)=8-E(ξ)=8-4=4,D(η)=(-1)2D(ξ)=2.4.6.已知ξ服从二项分布B(n,p),且E(3ξ+2)=9.2,D(3ξ+2)=12.96,则二项分布的参数n,p的值为(B)A.n=4,p=0.6B.n=6,p=0.4C.n=8,p=0.3D.n=24,p=0.1解析:E(3ξ+2)=3E(ξ)+2=3np+2=9.2,∴np=2.4.D(3ξ+2)=9D(ξ)=12.96.∴D(ξ)=1.44,即np(1-p)=1.44.∴1-p=0.6.∴p=0.4,n=6.7.同时抛掷两枚均匀硬币10次,设两枚硬币同时出现反面向上的次数为X,则D(X)等于(A)A.B.C.D.5解析:由题意知,离散型随机变量X服从二项分布,设事件A=“两枚硬币同时出现反面向上”,则P(A)=C()2=,所以X~B(10,),故D(X)=10××=.8.已知A1,A2为两所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为,该同学一旦通过某所高校的考试,就不再参加其他高校的考试,设该同学通过考试的高校个数为随机变量X,则D(X)=(A)A.B.C.D.解析:由已知X的取值可能为0,1.P(X=0)=×=,P(X=1)=+×=,∴E(X)=0×+1×=,D(X)=×+×=.二、填空题(每小题6分,共计18分)9.若随机变量ξ的分布列如下:ξ01xPp若E(ξ)=1.1,则D(ξ)=0.49.解析:先确定x、p,由分布列性质得p=1-(+)=,E(ξ)=0×+1×+x×=1.1,解得x=2,可得D(ξ)=(0-1.1)2×+(1-1.1)2×+(2-1.1)2×=0.49.10.随机变量ξ的分布列为:ξ-101Pabc其中a,b,c成等差数列,若E(ξ)=,则D(ξ)的值是.解析:由已知得解得所以,D(ξ)=(-1-)2×+(0-)2×+(1-)2×=.11.从学校乘汽车到火车站的途中有3个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是,设ξ为途中遇到红灯的次数,则离散型随机变量ξ的方差为.解析:由题意知ξ~B(3,),所以D(ξ)=3××=.三、解答题(共计22分)12.(10分)有10张卡片,其中8张标有数字2,有2张标有数字5,从中随机地抽取3张卡片,设3张卡片上的数字和为ξ,求E(ξ)与D(ξ).解:这3张卡片上的数字和ξ这一随机变量的可能取值为6,9,12,且“ξ=6”表示取出的3张卡片上都标有2,则P(ξ=6)==;“ξ=9”表示取出的3张卡片上有两张为2,一张为5,则P(ξ=9)==;“ξ=12”表示取出的3张卡片上有两张为5,一张为2,则P(ξ=12)==.∴ξ的分布列为ξ6912P则期望E(ξ)=6×+9×+12×=7.8,方差D(ξ)=×(6-7.8)2+×(9-7.8)2+×(12-7.8)2=3.36.13.(12分)如图所示是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图.(1)求直方图中x的值;(2)若将频率视为概率,从这个城市中随机抽取3位居民(看作有放回抽样),求月均用水量在3吨至4吨的居民数X的分布列、数学期...