高中数学 第三章 第4节简单的线性规划知识精讲 北师大版必修5VIP免费

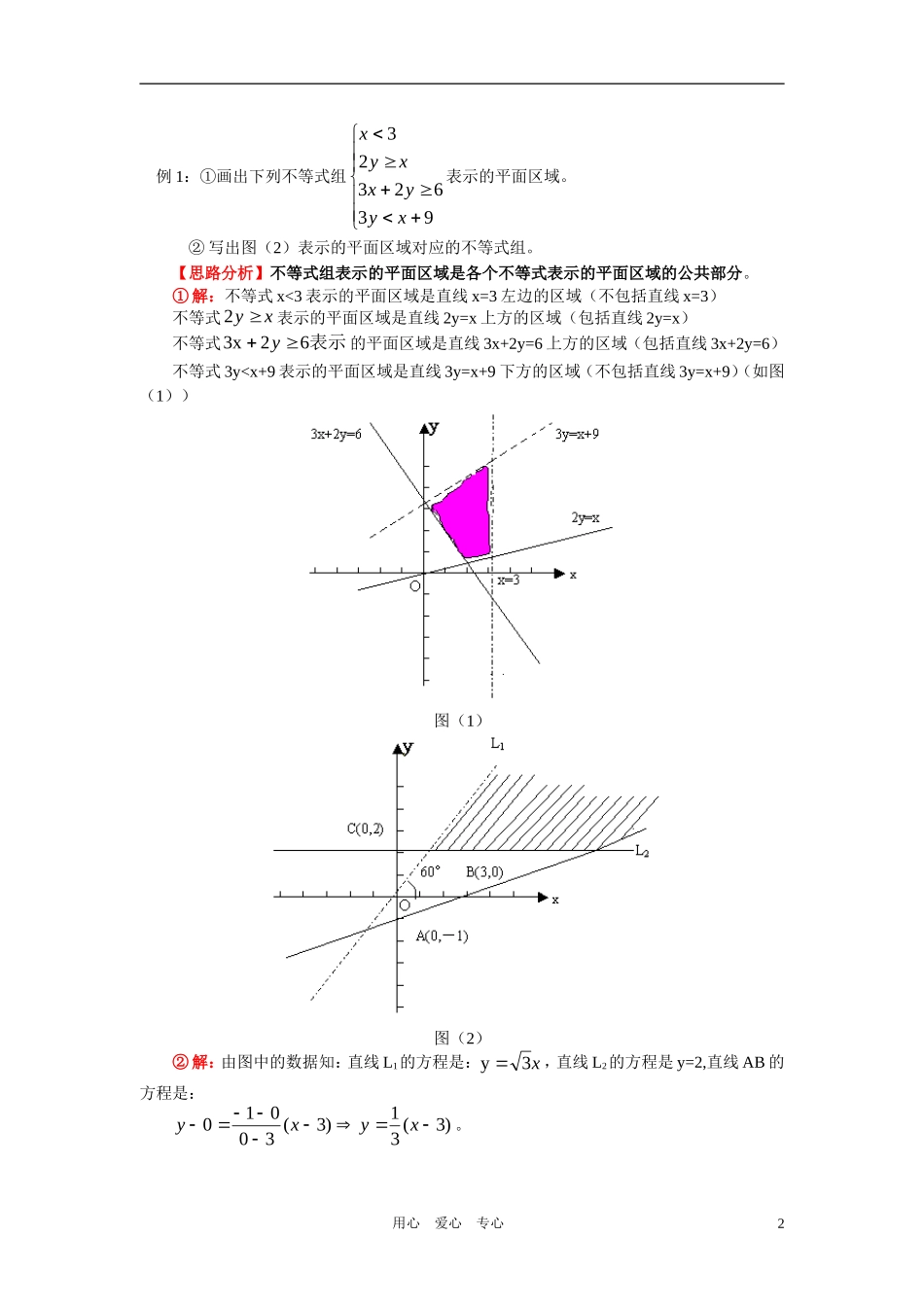
高二数学第三章第4节简单的线性规划知识精讲北师大版必修5【本讲教育信息】一、教学内容：简单的线性规划二、教学目标：（1）了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组，并能利用二元一次不等式组表示的平面区域解决简单的实际问题。（2）了解线性规划的意义，知道目标函数、约束条件、可行解、最优解等基本概念，能正确的利用图解法中的求解程序解决线性规划问题。（3）能建立二元线性规划数学模型解决简单的实际问题。三、知识要点分析：1.二元一次不等式（组）表示的平面区域（1）直线0:CByAxl把平面内不在直线上的点分成两部分，同一侧的点的坐标代入Ax+By+C中的值的符号相同，异侧的点的坐标代入Ax+By+C中的值的符号相反。（2）对于直线:lAx+By+C=0当B≠0时，可化为：y=kx+b的形式。对于二元一次不等式bkxy表示的平面区域是直线y=kx+b的上方（包括直线y=kx+b）.对于二元一次不等式bkxy表示的平面区域是直线y=kx+b的下方（包括直线y=kx+b）注意：二元一次不等式)0(0CByAx或与二元一次不等式)0(0CByAx表示的平面区域不同，前者不包括直线Ax+By+C=0,后者包括直线Ax+By+C=0.2.线性规划求线性目标函数在线性目标条件下的最值问题称为线性规划问题。基本步骤是：（1）确定好线性约束条件，准确画出可行域。（2）对目标函数z=ax+by,若b>0，则bz取得最大值（或最小值）时，z也取得最大值或最小值；若b<0,则反之。（3）一般地，可行域的边缘点有可能是最值点，有些问题可代入边缘点找最值.（4）注意实际问题的特殊要求。【典型例题】考点一：有关平面区域的问题用心爱心专心1例1：①画出下列不等式组9362323xyyxxyx表示的平面区域。②写出图（2）表示的平面区域对应的不等式组。【思路分析】不等式组表示的平面区域是各个不等式表示的平面区域的公共部分。①解：不等式x<3表示的平面区域是直线x=3左边的区域（不包括直线x=3）不等式xy2表示的平面区域是直线2y=x上方的区域（包括直线2y=x）不等式表示62x3y的平面区域是直线3x+2y=6上方的区域（包括直线3x+2y=6）不等式3y0,y>0时，不等式化为：4xy，（ii）x<0，y<0时，不等式化为：4yx（iii）,x>0,y<0时，不等式化为：4yx,（iv）,x<0,y>0时，不等式化为：4yx。针对上述四种情形：画出可行域如图（2）。按x,y取整数连成网格找格点。共有：41212325279个。平面区域是一个边长为24的正方形。故所求平面区域的面积是32图（1）图（2）考点三：求线性及非线性目标函数的最值问题例3：已知0520402yxyxyx求下列目标函数的最值或取值范围。（1）求z=x+2y－4的最大值。（2）求2510z22yyx的最小值。（3）求用心爱心专心3112xyz的取值范围。【思路分析】（1）只要求出线性目标p=x+2y的最大值就可以求出z的最大值。（2）2510z22yyx=（x－0）2+（y－5）2,故z可以看作可行域内任意一点P（x,y）到定点Q（0,5）的距离的平方。即要求z的最小值，只需求|PQ|2的最小值。（3）由112xyz=)1()21(2xy知：z表示...