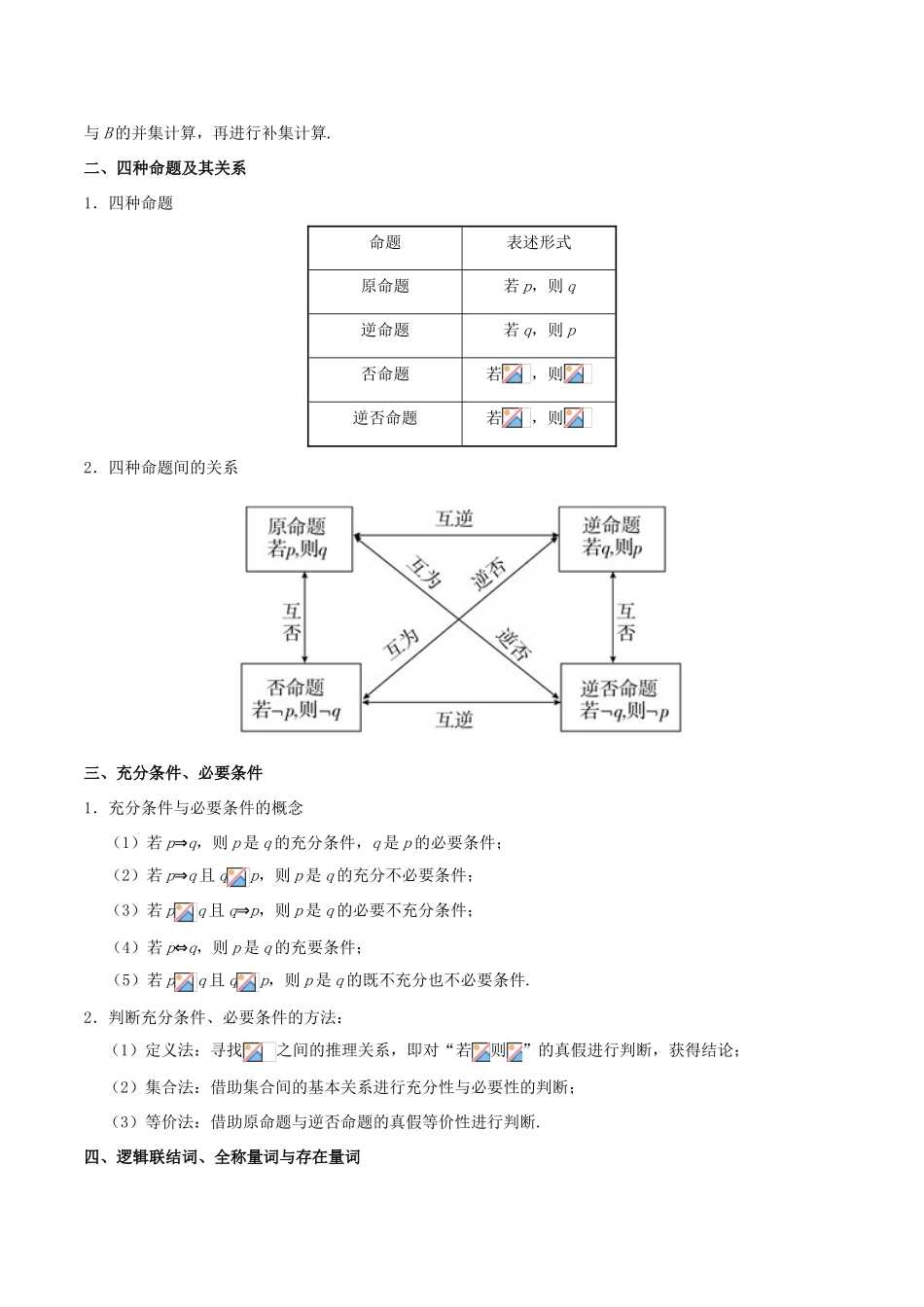
专题01集合与常用逻辑用语一、集合1.元素与集合之间有且仅有“属于()”和“不属于()”两种关系,且两者必居其一.2.集合中元素的特性:确定性、互异性、无序性.3.常用数集及其记法:集合非负整数集(自然数集)正整数集整数集有理数集实数集复数集符号或注意:实数集不能表示为{x|x为所有实数}或{},因为“{}”包含“所有”“全体”的含义.4.理解子集、真子集的概念,知道由“若,有”得是的子集,记作;上述条件下,若“,”得是的真子集,记作.注意子集表示符号“”与元素和集合关系符号“”的区别.5.给定一个集合,能够写出其子集、真子集、非空子集的个数,如给定集合的元素个数为,则其子集、真子集、非空子集的个数分别为.6.交集:,取两个集合的公共元素组成集合;并集:,取两个集合所有元素组成集合;补集:,取全集中不属于集合A的元素组成集合.注意:(1)空集不含任何元素,在解题过程中容易被忽略,特别是在隐含有空集参与的集合问题中,往往容易因忽略空集的特殊性而导致漏解.(2)集合的运算顺序,如表示先计算A的补集,再进行并集计算;则表示先进行A与B的并集计算,再进行补集计算.二、四种命题及其关系1.四种命题命题表述形式原命题若p,则q逆命题若q,则p否命题若,则逆否命题若,则2.四种命题间的关系三、充分条件、必要条件1.充分条件与必要条件的概念(1)若p⇒q,则p是q的充分条件,q是p的必要条件;(2)若p⇒q且qp,则p是q的充分不必要条件;(3)若pq且q⇒p,则p是q的必要不充分条件;(4)若p⇔q,则p是q的充要条件;(5)若pq且qp,则p是q的既不充分也不必要条件.2.判断充分条件、必要条件的方法:(1)定义法:寻找之间的推理关系,即对“若则”的真假进行判断,获得结论;(2)集合法:借助集合间的基本关系进行充分性与必要性的判断;(3)等价法:借助原命题与逆否命题的真假等价性进行判断.四、逻辑联结词、全称量词与存在量词1.常见的逻辑联结词:或、且、非一般地,用联结词“且”把命题p和q联结起来,得到一个新命题,记作,读作“p且q”;用联结词“或”把命题p和q联结起来,得到一个新命题,记作,读作“p或q”;对一个命题p的结论进行否定,得到一个新命题,记作,读作“非p”.2.复合命题的真假判断“p且q”“p或q”“非p”形式的命题的真假性可以用下面的表(真值表)来确定:pq真真假假真真真假假真真假假真真假真假假假真真假假3.全称量词和存在量词量词名称常见量词符号表示全称量词所有、一切、任意、全部、每一个等存在量词存在一个、至少一个、有些、某些等4.含有一个量词的命题的否定全称命题的否定是特称命题,特称命题的否定是全称命题,如下所示:命题命题的否定一、考查集合间的基本关系【例1】已知集合,则集合的子集的个数为A.B.C.D.【答案】B【解析】集合,,故集合的子集的个数为.故选B.【名师点睛】对于集合间的基本关系,高考中一般考查求子集的个数或由集合间的关系求参数的取值范围问题.二、考查集合的基本运算【例2】已知集合,,则A.B.C.D.【答案】C【解析】由已知得,则,又,故,故选C.【例3】已知集合,,则A.B.C.D.【答案】C【解析】 集合,∴. 集合,∴,,,.故选C.【名师点睛】集合间的运算问题,常和函数等其他知识相结合,求解时注意区分是求有限集间集合的运算还是无限集间集合的运算,若是有限集间集合的运算问题,一般使用定义法和Venn图法;若是无限集间集合的运算,则一般用数轴求解.三、充分条件、必要条件【例4】已知条件p:函数的定义域,条件,则是的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】依题意,要使函数有意义,则,得或,故命题:或.由得,则,则,但p不能推出q,故是的充分不必要条件.【例5】已知,,若的一个充分不必要条件是,则实数的取值范围是A.B.C.D.【答案】A【解析】由基本不等式得,,由,又因为的一个充分不必要条件是,则,故选A.【名师点睛】注意区分A是B的充分条件与A的充分条件是B:(1)“A的充分不必要条件是B”是指B能推出A,且A不能推出B,即B⇒A且AB;(2)“A是B的充分不必要条...