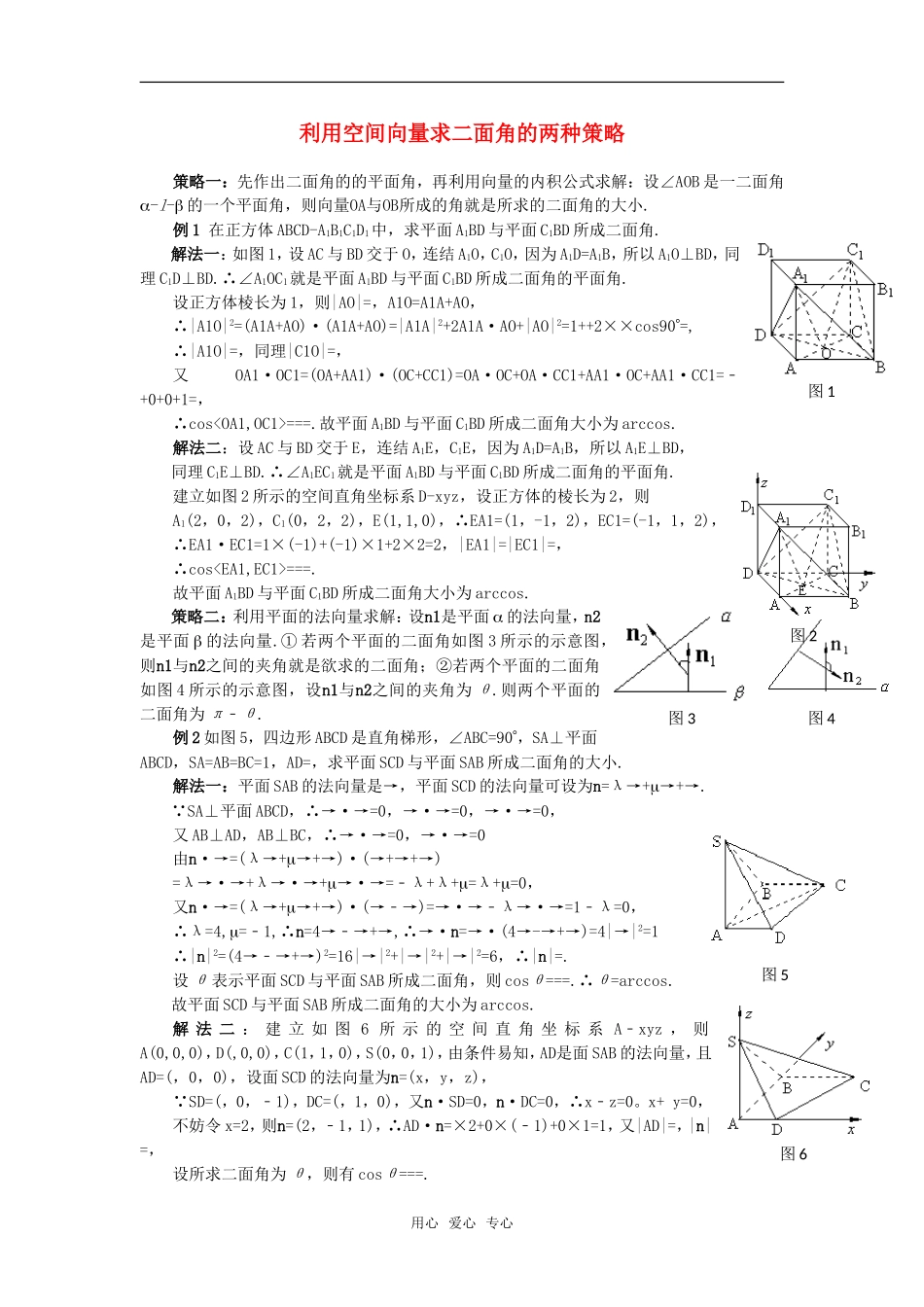
利用空间向量求二面角的两种策略策略一:先作出二面角的的平面角,再利用向量的内积公式求解:设∠AOB是一二面角a-l-b的一个平面角,则向量OA与OB所成的角就是所求的二面角的大小.例1在正方体ABCD-A1B1C1D1中,求平面A1BD与平面C1BD所成二面角.解法一:如图1,设AC与BD交于O,连结A1O,C1O,因为A1D=A1B,所以A1O⊥BD,同理C1D⊥BD.∴∠A1OC1就是平面A1BD与平面C1BD所成二面角的平面角.设正方体棱长为1,则|AO|=,A1O=A1A+AO,∴|A1O|2=(A1A+AO)·(A1A+AO)=|A1A|2+2A1A·AO+|AO|2=1++2××cos90°=,∴|A1O|=,同理|C1O|=,又OA1·OC1=(OA+AA1)·(OC+CC1)=OA·OC+OA·CC1+AA1·OC+AA1·CC1=﹣+0+0+1=,∴cos===.故平面A1BD与平面C1BD所成二面角大小为arccos.解法二:设AC与BD交于E,连结A1E,C1E,因为A1D=A1B,所以A1E⊥BD,同理C1E⊥BD.∴∠A1EC1就是平面A1BD与平面C1BD所成二面角的平面角.建立如图2所示的空间直角坐标系D-xyz,设正方体的棱长为2,则A1(2,0,2),C1(0,2,2),E(1,1,0),∴EA1=(1,-1,2),EC1=(-1,1,2),∴EA1·EC1=1×(-1)+(-1)×1+2×2=2,|EA1|=|EC1|=,∴cos===.故平面A1BD与平面C1BD所成二面角大小为arccos.策略二:利用平面的法向量求解:设n1是平面a的法向量,n2是平面b的法向量.①若两个平面的二面角如图3所示的示意图,则n1与n2之间的夹角就是欲求的二面角;②若两个平面的二面角如图4所示的示意图,设n1与n2之间的夹角为θ.则两个平面的二面角为π﹣θ.例2如图5,四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=,求平面SCD与平面SAB所成二面角的大小.解法一:平面SAB的法向量是→,平面SCD的法向量可设为n=λ→+→+→.∵SA⊥平面ABCD,∴→·→=0,→·→=0,→·→=0,又AB⊥AD,AB⊥BC,∴→·→=0,→·→=0由n·→=(λ→+→+→)·(→+→+→)=λ→·→+λ→·→+→·→=﹣λ+λ+=λ+=0,又n·→=(λ→+→+→)·(→﹣→)=→·→﹣λ→·→=1﹣λ=0,∴λ=4,=﹣1,∴n=4→﹣→+→,∴→·n=→·(4→-→+→)=4|→|2=1∴|n|2=(4→﹣→+→)2=16|→|2+|→|2+|→|2=6,∴|n|=.设θ表示平面SCD与平面SAB所成二面角,则cosθ===.∴θ=arccos.故平面SCD与平面SAB所成二面角的大小为arccos.解法二:建立如图6所示的空间直角坐标系A﹣xyz,则A(0,0,0),D(,0,0),C(1,1,0),S(0,0,1),由条件易知,AD是面SAB的法向量,且AD=(,0,0),设面SCD的法向量为n=(x,y,z),∵SD=(,0,﹣1),DC=(,1,0),又n·SD=0,n·DC=0,∴x﹣z=0。x+y=0,不妨令x=2,则n=(2,﹣1,1),∴AD·n=×2+0×(﹣1)+0×1=1,又|AD|=,|n|=,设所求二面角为θ,则有cosθ===.用心爱心专心图3图4图5图1图2图6故平面SCD与平面SAB所成二面角的大小为arccos.用心爱心专心