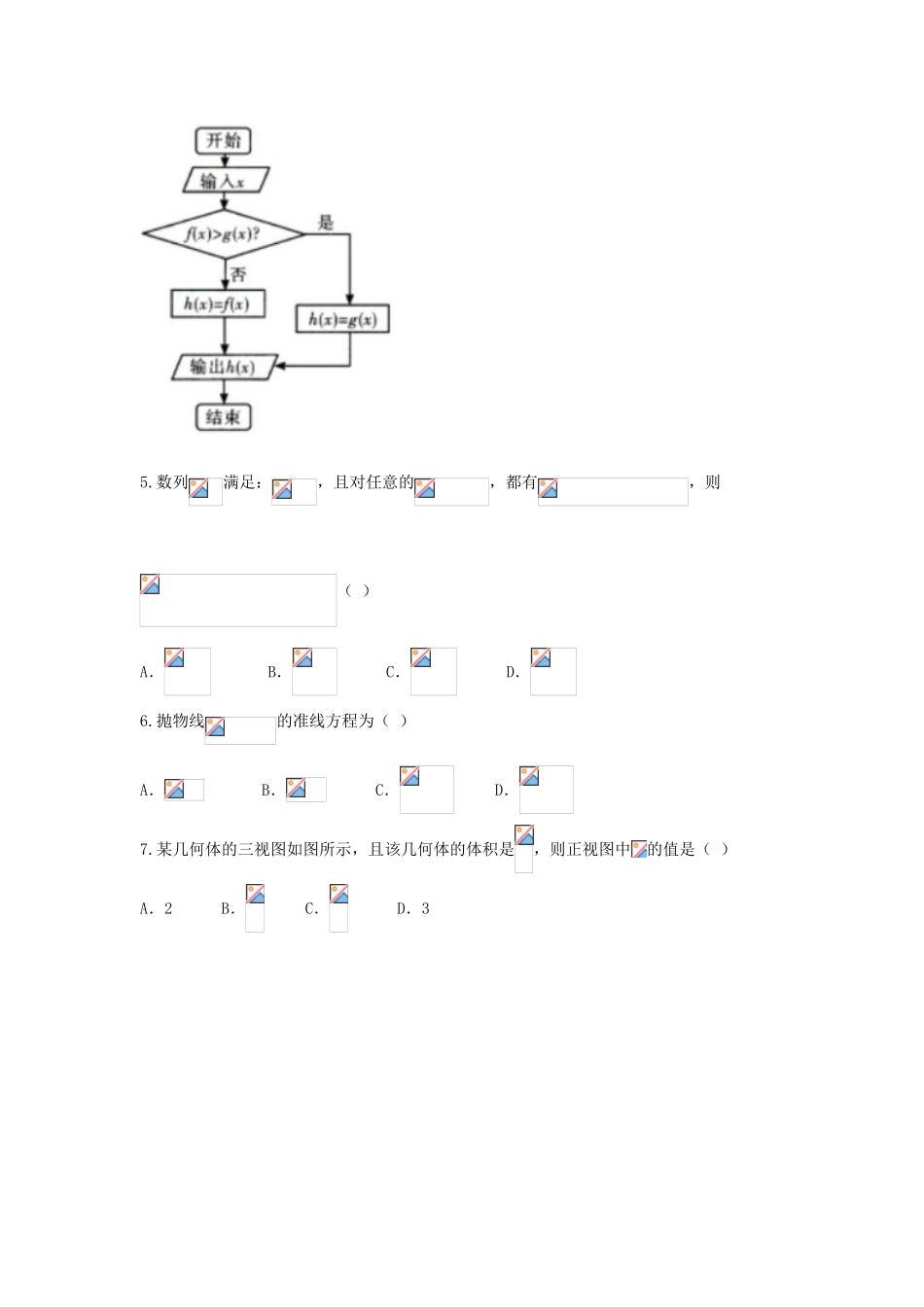
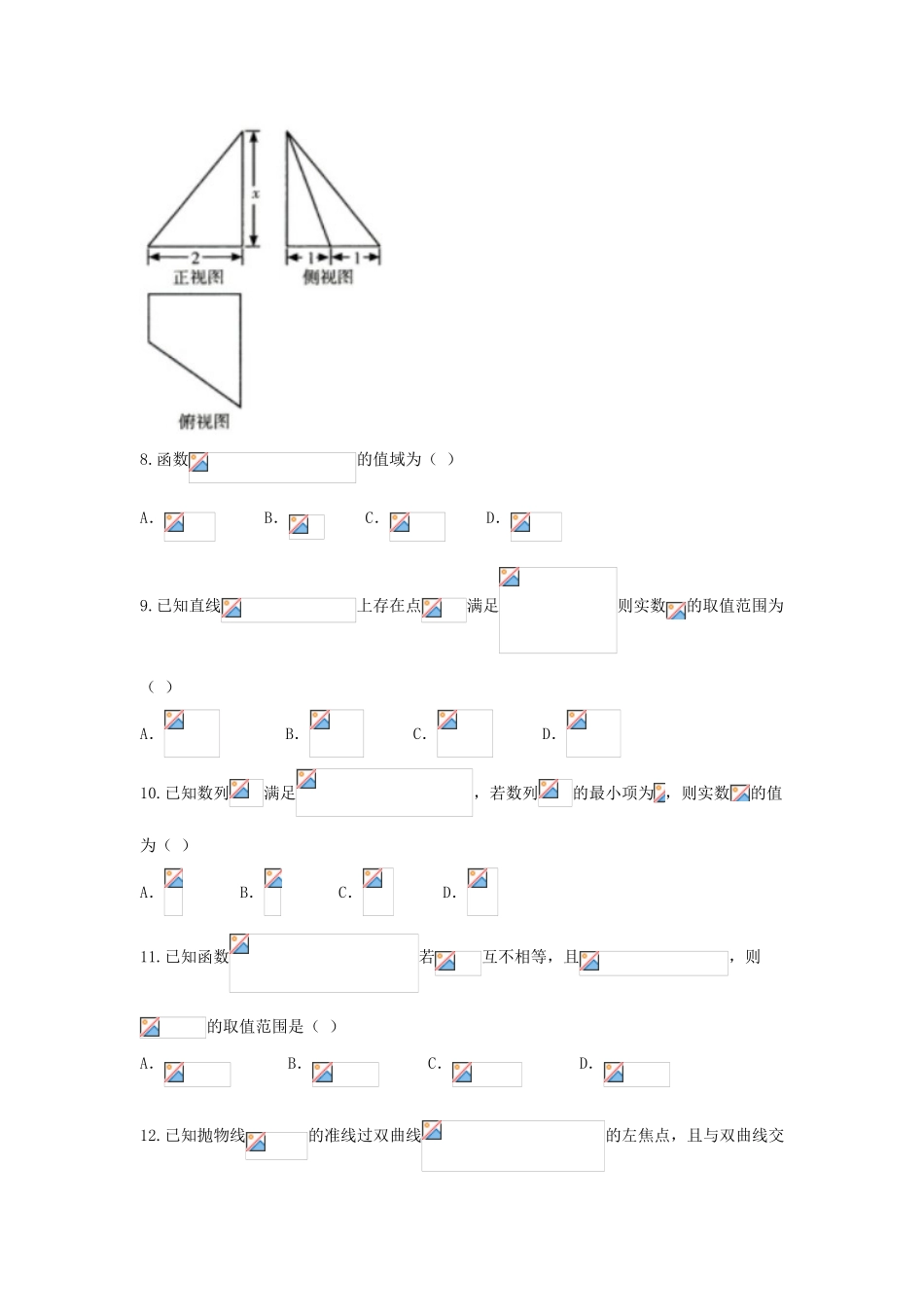
河南省郑州一中2016届高三数学考前冲刺卷(一)文第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集,集合,集合,则()A.[1,2]B.[1,2)C.(1,2]D.(1,2)2.i是虚数单位,复数()A.B.1+iC.iD.-i3.若直线与圆相交于A,B两点,则“k=1”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.如图,若,输入,则输出()A.0.25B.C.D.-25.数列满足:,且对任意的,都有,则()A.B.C.D.6.抛物线的准线方程为()A.B.C.D.7.某几何体的三视图如图所示,且该几何体的体积是,则正视图中的值是()A.2B.C.D.38.函数的值域为()A.B.C.D.9.已知直线上存在点满足则实数的取值范围为()A.B.C.D.10.已知数列满足,若数列的最小项为,则实数的值为()A.B.C.D.11.已知函数若互不相等,且,则的取值范围是()A.B.C.D.12.已知抛物线的准线过双曲线的左焦点,且与双曲线交于两点,为坐标原点,的面积为,则双曲线的离心率为()A.B.4C.3D.2第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.在中,点M是边BC的中点.若,则的最小值是_____.14.若,且,则的值为_____.15.在半径为2的球面上有不同的四点A,B,C,D,若AB=AC=AD=2,则平面BCD被球所截得图形的面积为________.16.已知函数在区间上单调递增,则实数的取值范围是_____.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)已知a,b,c分别是△ABC的角A,B,C所对的边,且.(1)若△ABC的面积等于,求a,b的值;(2)若,求A的值.18.(本小题满分12分)如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.(1)求此人到达当日空气重度污染的概率;(2)求此人停留期间空气质量至少有1天为优良的概率;(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)19.(本小题满分12分)如图所示,已知直三棱柱中,分别是的中点,点P在线段上运动.(1)证明:无论点P在线段上的任何位置,总有AM⊥平面PNQ;(2)若AC=1,求三棱锥P-MNQ的体积.20.(本小题满分12分)已知为椭圆C的左、右焦点,且点在椭圆C上.(1)求椭圆C的方程;(2)过的直线交椭圆C于A,B两点,则的内切圆的面积是否存在最大值?若存在,求其最大值及此时的直线方程;若不存在,请说明理由.21.(本小题满分12分)设,函数.(1)若,求函数的单调区间;(2)当时,函数取得极值,证明:对于任意,.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4-1:几何证明选讲如图所示,圆O的直径AB=10,P是AB延长线上的一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.(1)求证:PEC=PDF;(2)求的值.23.(本小题满分10分)选修4-4:坐标系与参数方程极坐标与直角坐标系xOy有相同的长度单位,以坐标原点O为极点,以x轴的正半轴为极轴,已知曲线C的极坐标方程为.(1)将曲线C的极坐标方程化为参数方程;(2)已知曲线C上两点,求△AOB的面积的最小值及此时的值.24.(本小题满分10分)选修4-5:不等式选讲已知正实数a,b满足a+b=2.(1)求的最小值m;(2)设函数,对于(1)中求得的,是否存在实数,使得成立?若存在,求出x的取值范围;若不存在,说明理由.数学(文科)试卷(一)参考答案1-5DCADD6-12DCAABCD13.14.1或15.16.[-1,1]17.(1)根据三角形的面积公式可知:,所以ab=4.又由余弦定理可知:,所以.综上可得a=b=2.(2)因为,所以,当时,.当时,.由正弦定理得.联立得.根据题意,得,且与互斥,i,j=1,2,3,...,13,i≠j.(1)设B表示事件“此人到达当日空气重度污染”,则.所以.(2)设此人停留期间刚好有一天空气质量优良的事件为C,刚好有两天空气质量优良的事件为D,则,.所以此人停留期间空气质量...