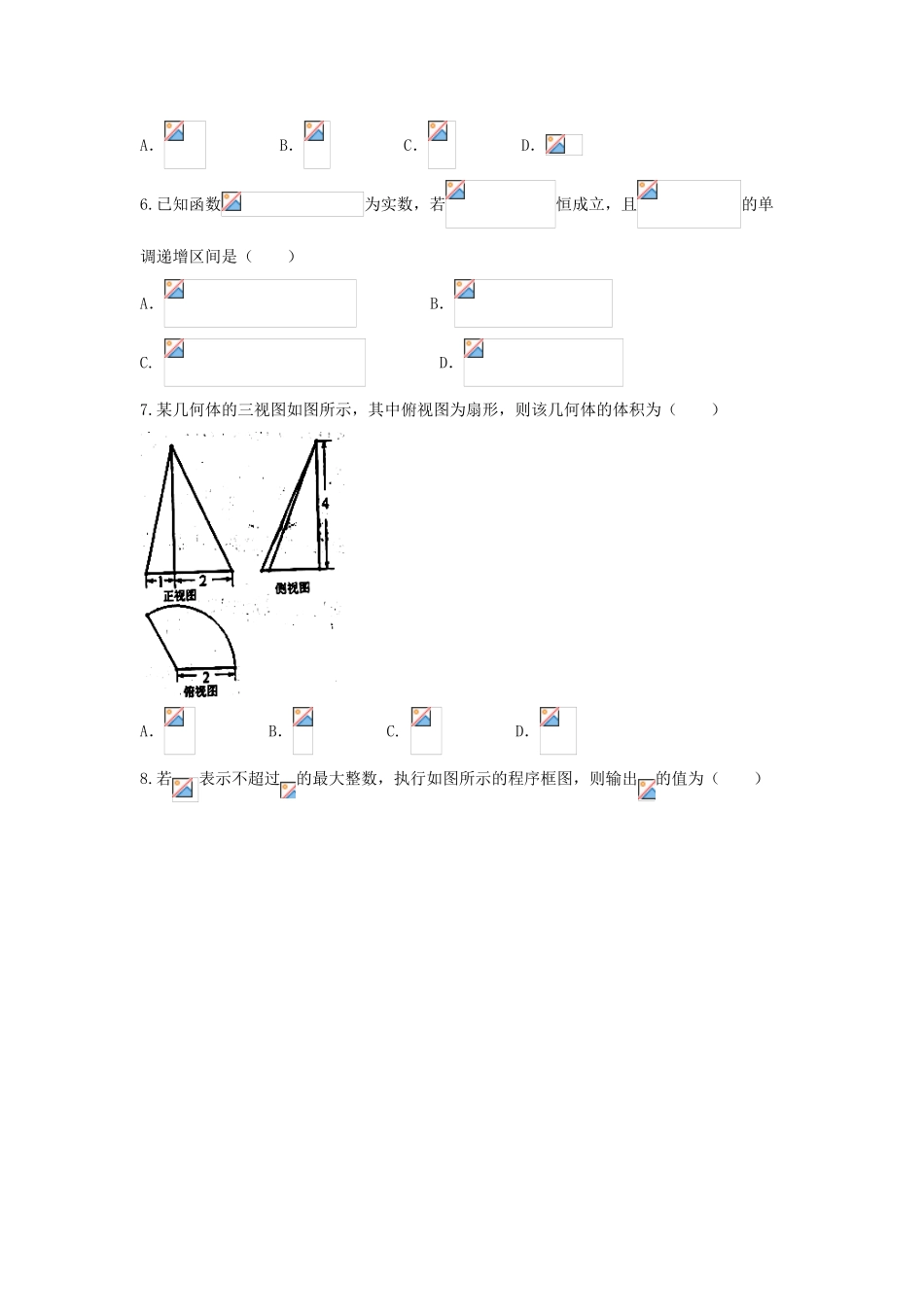
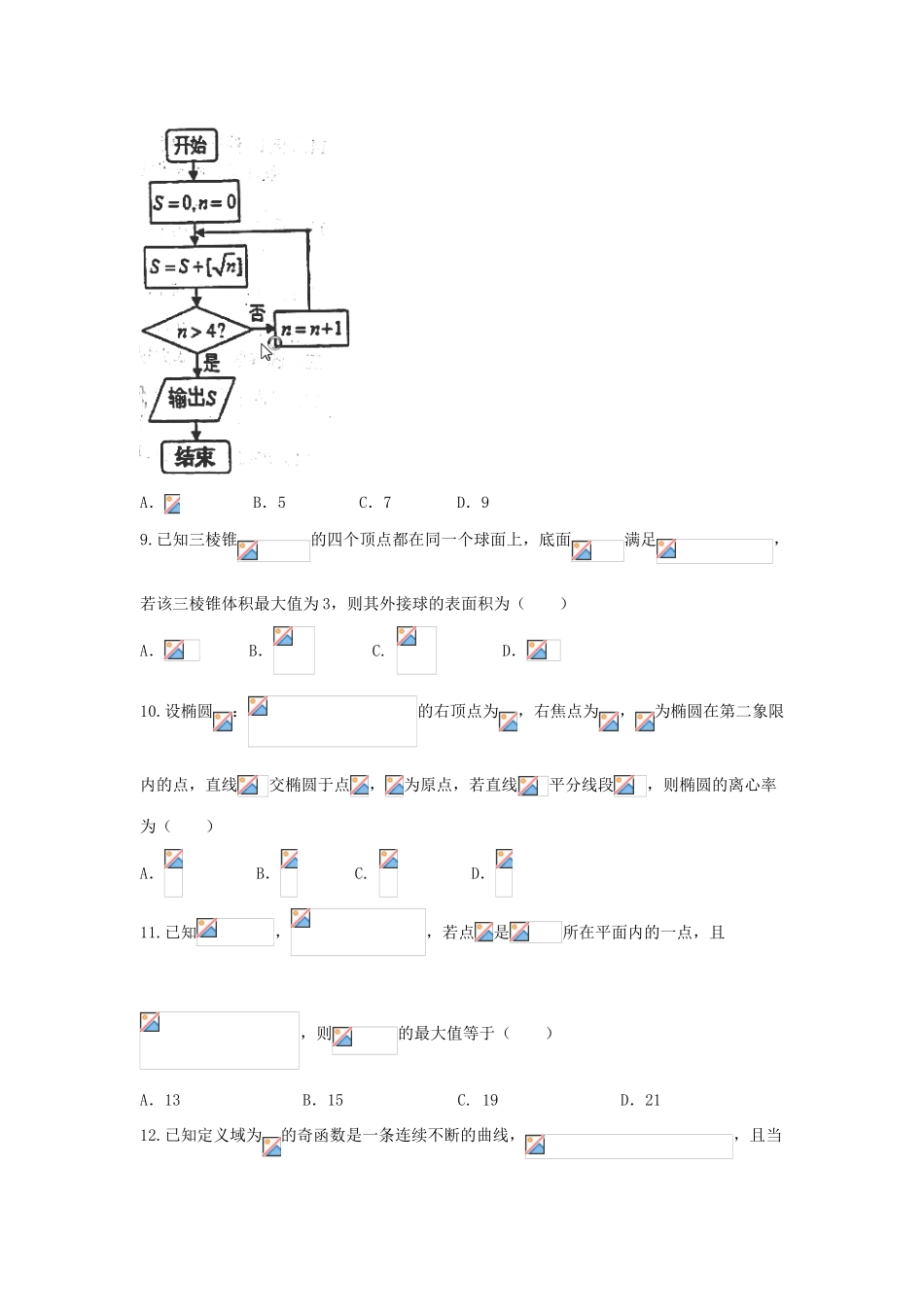
辽宁省庄河市2018届高三数学上学期开学考试试题理第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.,则()A.B.C.D.2.已知集合,,,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.即不充分也不必要条件3.古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是()A.该金锤中间一尺重3斤B.中间三尺的重量和是头尾两尺重量和的3倍C.该金锤的重量为15斤D.该金锤相邻两尺的重量之差的绝对值为0.5斤4.已知某次数学考试的成绩服从正态分布,则114分以上的成绩所占的百分比为()(附,,)A.B.C.D.5.已知函数,则的值为()A.B.C.D.6.已知函数为实数,若恒成立,且的单调递增区间是()A.B.C.D.7.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为()A.B.C.D.8.若表示不超过的最大整数,执行如图所示的程序框图,则输出的值为()A.B.5C.7D.99.已知三棱锥的四个顶点都在同一个球面上,底面满足,若该三棱锥体积最大值为3,则其外接球的表面积为()A.B.C.D.10.设椭圆:的右顶点为,右焦点为,为椭圆在第二象限内的点,直线交椭圆于点,为原点,若直线平分线段,则椭圆的离心率为()A.B.C.D.11.已知,,若点是所在平面内的一点,且,则的最大值等于()A.13B.15C.19D.2112.已知定义域为的奇函数是一条连续不断的曲线,,且当时,导函数,则在区间上的最小值为()A.B.0C.D.2016第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设变量满足约束条件,则目标函数的最大值为.14.若10件产品包含2件次品,今在其中任取两件,已知两件中有一件不是废品的条件下,另一件是废品的概率为.15.设,则的值是.16.在中,角的对边分别为.已知,且,则的面积的最大值为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.为数列的前项和,已知,.(1)求数列的通项公式;(2)设,求数列的前项的和.18.某市规定,高中学生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段(单位:小时)进行统计,其频率分布直方图如图所示.(1)求抽取的200为学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;(2)从全市高中学生(人数很多)中任意选取3为学生,记为3为学生中参加社区服务时间不少于90小时的人数.试求随机变量的分布列和数学期望和方差.19.如图,四棱锥,侧面是边长为2的正三角形,且与底面垂直,底面是的菱形,为棱上的动点,且.(1)求证:;(2)试确定的值,使得二面角的平面角余弦值为.20.已知椭圆的两个焦点,动点在椭圆上,且使得的点恰有两个,动点到焦点的距离的最大值为.(1)求椭圆的方程;(2)如图,以椭圆的长轴为直径作圆,过直线上的动点作圆的两条切线,设切点分别为,若直线与椭圆交于不同的两点,求的取值范围.21.已知函数.(1)若,求曲线在点处的切线方程;(2)若在处取得最小值,求实数的取值范围.22.已知极坐标系的极点为平面直角坐标系的原点,极轴为轴的正半轴,两种坐标系中的长度单位相同,曲线的参数方程为(为参数),直线过点,且斜率为,射线的极坐标方程为.(1)求曲线和直线的极坐标方程;(2)已知射线与圆的交点为,与直线的交点为,求线段的长.试卷答案一、选择题1-6:AABDBC7-12:DCDBAC二、填空题13.214.15.4016.三、解答题17.(1)由题知,为数列的前项和,,则两式相减可得,整理可得,又,则,则有,当时,,解得或(舍去)则数列是以3为首项,2为公差的等差数列,则综上所述,结论是:数列的通项公式为;(2)由(1)得,,则则数列的前项的和为:综上所述,结论是:数列的前项的和为.18.解:(1)根据题意,参加社区服务时...