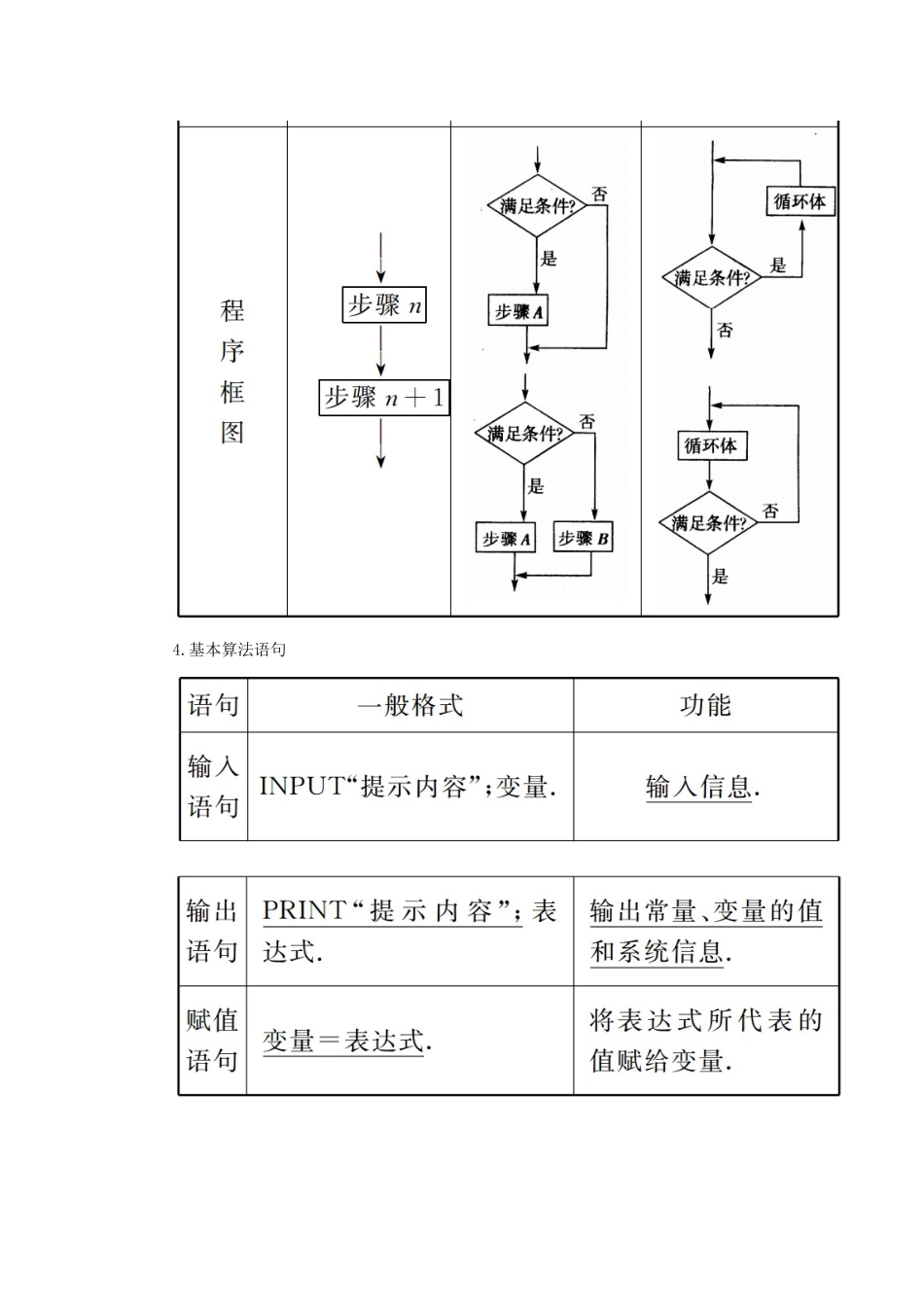
第一节算法与程序框图【最新考纲】1.了解算法的含义,了解算法的思想.2.理解程序框图的三种基本逻辑结构:顺序、条件、循环.3.理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.1.算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.(2)应用:算法通常可以编成计算机程序,让计算机执行并解决问题.2.程序框图定义:程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.3.三种基本逻辑结构4.基本算法语句1.(质疑夯基)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)程序框图中的图形符号可以由个人来确定.()(2)一个程序框图一定包含顺序结构,但不一定包含条件结构和循环结构.()(3)“当型”循环与“直到型”循环退出循环的条件不同.()(4)在算法语句中,X=X+1是错误的.()答案:(1)×(2)√(3)√(4)×2.根据给出的程序框图,计算f(-1)+f(2)=()A.0B.1C.2D.4解析:输入-1,满足x≤0,所以f(-1)=4×(-1)=-4;输入2,不满足x≤0,所以f(2)=22=4,即f(-1)+f(2)=0.答案:A3.(2015·陕西卷)根据右边框图,当输入x为2006时,输出的y=()A.2B.4C.10D.28解析:x每执行一次循环减少2,当x变为-2时跳出循环,y=3-x+1=32+1=10.答案:C4.某程序框图如图所示,若输出的S=57,则判断框内为()A.k>4?B.k>5?C.k>6?D.k>7?解析:由程序框图可知,k=1时,S=1;k=2时,S=2×1+2=4;k=3时,S=2×4+3=11;k=4时,S=2×11+4=26;k=5时,S=2×26+5=57.答案:A5.阅读如图所示的程序框图,运行相应的程序,输出的S的值等于________.解析:第1次循环:S=0+21+1,此时S=3<15;第2次循环:S=3+22+2,此时S=9<15;第3次循环:S=9+23+3,此时S=20>15;终止循环,输出S=20.答案:20一条规律每个算法结构都含有顺序结构,循环结构中必定包含一个条件结构,用于确定何时终止循环体,循环结构和条件结构都含有顺序结构.一种区别当型循环与直到型循环的区别直到型循环是“先循环,后判断,条件满足时终止循环”;而当型循环则是“先判断,后循环,条件满足时执行循环”;两者的判断框内的条件表述在解决同一问题时是不同的它们恰好相反.两点注意1.赋值号左边只能是变量(不是表达式),在一个赋值语句中只能给一个变量赋值.2.利用循环结构表示算法,要明确是利用当型循环结构,还是直到型循环结构.要注意:(1)选择好累计变量;(2)弄清在哪一步开始循环,满足什么条件不再执行循环体.A级基础巩固一、选择题1.(2015·四川卷)执行如图所示的程序框图,输出S的值()A.-B.C.-D.解析:当k=5时,输出S=sin=sin=sin=.答案:D2.(2016·西安调研)根据框图(如图所示),对大于2的整数N,输出的数列的通项公式是()A.an=2nB.an=2(n-1)C.an=2nD.an=2n-1解析:第一次运行:i=1,a1=2×1=2,S=a1=2第二次运行:i=2,a2=2×2=22,S=a2=22.第三次运行:i=3,a3=2×22=23,S=a3=23.第四次运行:i=4,a4=2×23=24,S=a4=24.……∴an=2n.答案:C3.(2015·北京卷)执行如图所示的程序框图,输出的结果为()A.(-2,2)B.(-4,0)C.(-4,-4)D.(0,-8)解析:第一次循环:S=1-1=0,t=1+1=2,x=0,y=2,k=1.第二次循环:S=0-2=-2,t=0+2=2,x=-2,y=2,k=2;第三次循环:S=-2-2=-4,t=-2+2=0,x=-4,y=0,k=3.因此输出的点为(-4,0).答案:B4.(2014·课标全国Ⅰ卷)执行下面的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=()A.B.C.D.解析:第一次执行循环后:M=1+=,a=2,b=,n=2;第二次执行循环后:M=2+=,a=,b=,n=3.第三次执行循环后:M=+=,a=,b=,n=4.这时n=4,跳出循环,输出M的值.答案:D5.(2016·唐山质检)所示的程序框图,若输出k的值为6,则判断框内可填入的条件是()A.S>?B.S>?C.S>?D.S>?解析:第一次执行循环:s=1×=,k=8,s=应满足条件;第二次执行循环:s=×=,k=7,s=应满足条件,排除选项D;第三次执行循环:s=×=,k...