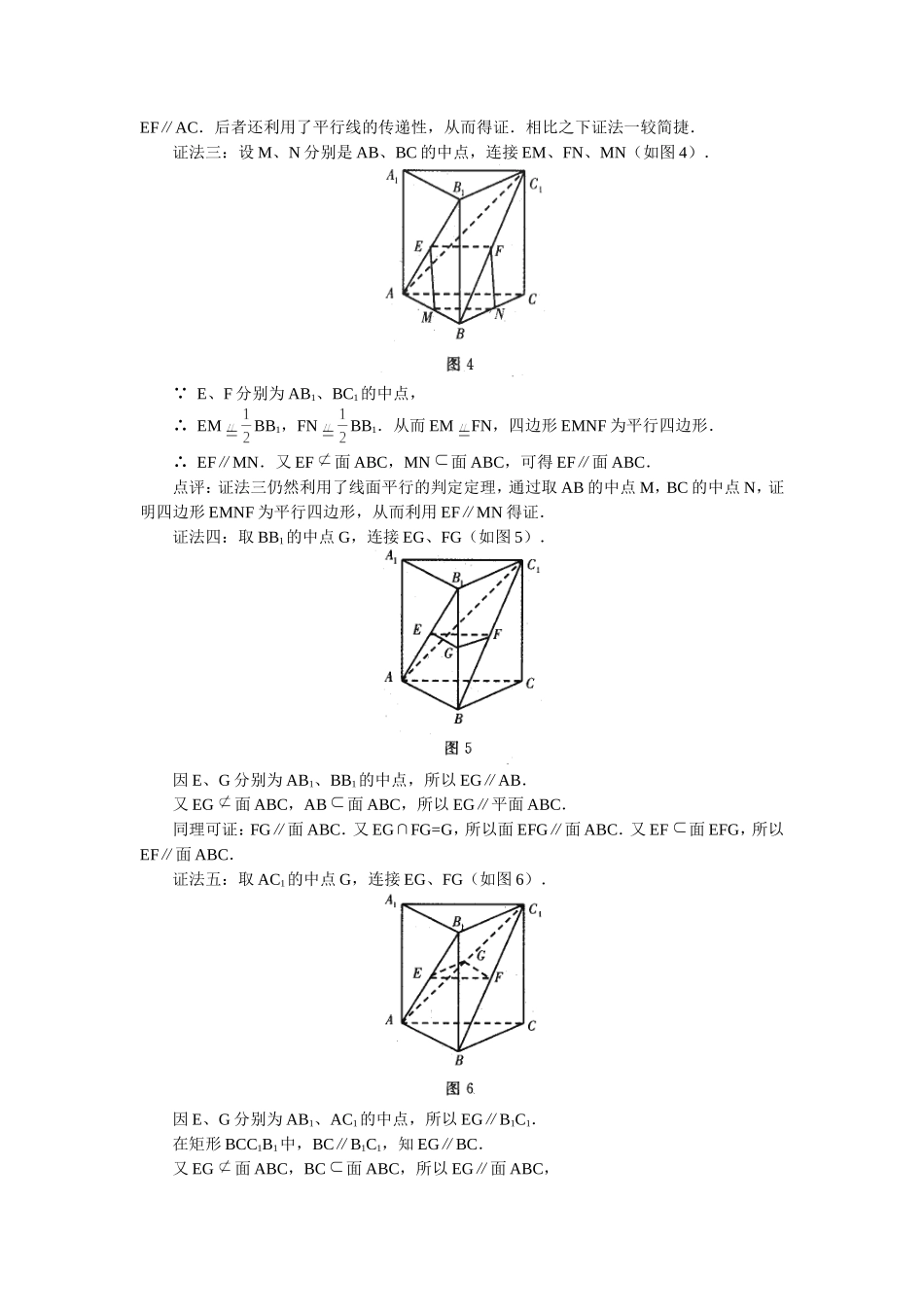
一题多解以点带面吴传叶新课标要求培养大家浓厚的学习兴趣,顽强的学习毅力,实事求是的科学态度,独立思考、勇于创新的精神和学习习惯.为此本文整理了一道立体几何题的五种证法,供广大读者参考.题目:如图1所示的空间图形中,已知四边形ABB1A1、ACC1A1、BCC1B1均为矩形,E、F分别是AB1、BC1的中点,求证:EF∥面ABC.证法一:连接B1C(如图2),因为四边形BCC1B1为矩形,F是BC1的中点,所以B1C过点F,且F是B1C的中点.E是AB1的中点,在△AB1C中,EF∥AC.又EF面ABC,AC面ABC,所以EF∥面ABC.证法二:∵四边形BCC1B1为矩形,E是AB1的中点,∴连接A1B(如图3),A1B过点E,且E是A1B的中点.由F是BC1的中点,所以在△A1BC1中,EF∥A1C1.在矩形ACC1A1中,AC∥A1C1,所以EF∥AC.又EF面ABC,AC面ABC,故EF∥面ABC.点评:证法一和证法二都利用了线面平行的判定定理,两者都通过添加辅助线,证明EF∥AC.后者还利用了平行线的传递性,从而得证.相比之下证法一较简捷.证法三:设M、N分别是AB、BC的中点,连接EM、FN、MN(如图4).∵E、F分别为AB1、BC1的中点,∴EMBB1,FNBB1.从而EMFN,四边形EMNF为平行四边形.∴EF∥MN.又EF面ABC,MN面ABC,可得EF∥面ABC.点评:证法三仍然利用了线面平行的判定定理,通过取AB的中点M,BC的中点N,证明四边形EMNF为平行四边形,从而利用EF∥MN得证.证法四:取BB1的中点G,连接EG、FG(如图5).因E、G分别为AB1、BB1的中点,所以EG∥AB.又EG面ABC,AB面ABC,所以EG∥平面ABC.同理可证:FG∥面ABC.又EG∩FG=G,所以面EFG∥面ABC.又EF面EFG,所以EF∥面ABC.证法五:取AC1的中点G,连接EG、FG(如图6).因E、G分别为AB1、AC1的中点,所以EG∥B1C1.在矩形BCC1B1中,BC∥B1C1,知EG∥BC.又EG面ABC,BC面ABC,所以EG∥面ABC,同理可证:FG∥面ABC.又EG∩FG=G,知面EFG∥面ABC.又EF面EFG,所以EF∥面ABC.点评:证法四和证法五都利用了面面平行的性质定理,证明了EF所在的平面EFG∥平面ABC,从而得证.作为普通的立体几何题,只要善于从不同的角度思考,总能找到不同的解决办法,这不仅能挖掘潜力,提高应变能力,同时还能对所学的数学知识作系统全面的复习.