江苏省昆山震川高级中学高三数学作业2 苏科版VIP免费

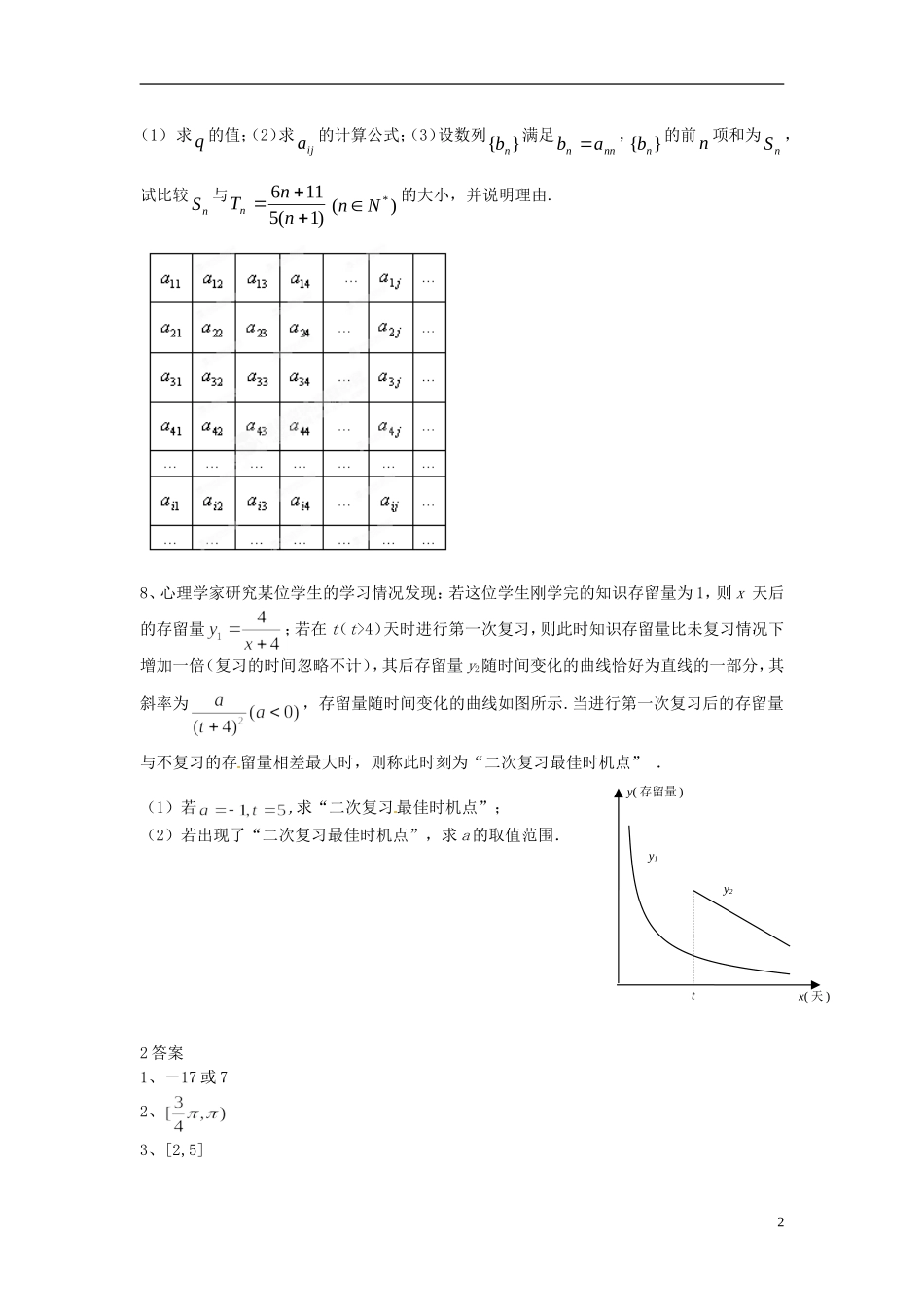
江苏省昆山震川高级中学高三数学作业2苏科版1、已知直线被圆所截的弦长为，则实数的值为__．2、已知点P是曲线上的一动点，为曲线在点P处的切线的倾斜角，则的取值范围为__．3、在平行四边形中，，边的长分别为2、1，若分别是边、上的点，且满足，则的取值范围是__．4、设实数，若不等式对任意都成立，则的最小值为__．6、如图,是边长为的正方形，平面，，.(1)求证：平面；(2)设点是线段上一个动点，试确定点的位置，使得平面，并证明你的结论.7、在下表中，每行上的数从左到右都成等比数列，并且所有公比都等于q，每列上的数从上到下都成等差数列．正数ija表示位于第i行第j列的数，其中8124a，142a，16554a．1ABCDFEy(存留量)x(天)y2y1t（1）求q的值；（2）求ija的计算公式；（3）设数列}{nb满足nnnab，}{nb的前n项和为nS，试比较nS与)1(5116nnTn)(*Nn的大小，并说明理由.8、心理学家研究某位学生的学习情况发现：若这位学生刚学完的知识存留量为1，则x天后的存留量；若在t（t>4）天时进行第一次复习，则此时知识存留量比未复习情况下增加一倍（复习的时间忽略不计），其后存留量y2随时间变化的曲线恰好为直线的一部分，其斜率为，存留量随时间变化的曲线如图所示.当进行第一次复习后的存留量与不复习的存留量相差最大时，则称此时刻为“二次复习最佳时机点”．（1）若,求“二次复习最佳时机点”；（2）若出现了“二次复习最佳时机点”，求a的取值范围．2答案1、－17或72、3、[2,5]24、5、6、解：(1)证明：因为平面，所以.因为是正方形，所以，因为从而平面.（2）当M是BD的一个三等分点，即3BM＝BD时，AM∥平面BEF．取BE上的三等分点N，使3BN＝BE，连结MN，NF，则DE∥MN，且DE＝3MN，因为AF∥DE，且DE＝3AF，所以AF∥MN，且AF＝MN，故四边形AMNF是平行四边形．所以AM∥FN，因为AM平面BEF，FN平面BEF，所以AM∥平面BEF．7、19．解：（1）设第4列公差为d，则161381165252454aad．故411611655444daa，于是4142442aaq．由于0ija，所以0q，故21q．（2）由于各列成等差数列，故在第4列中，iidiaai161)2(16181)2(244．由于第i行成等比数列，且公比21q，所以，jjjiijiiqaa)21()21(161444．（3）由（2）可知nnnna)21(．即nnnb)21(．所以nnbbbbS321.即nnnnnS)21()21()1()21(3)21(2211132，故1432)21()21()1()21(3)21(2)21(121nnnnnS．两式相减，得132)21()21()21()21(2121nnnnS11)21()21(1)21(211])21(1[21nnnnnn，3所以nnnnnnS22222121．因为0212)3()42(2222321111nnnnnnnnnnnSS（)Nn所以数列}{nS)(Nn是递增数列.同理)2)(1(5)2)(116()1)(176()1(5116)2(511)1(61nnnnnnnnnnTTnn0)2)(1(55nn)(Nn所以}{nT)(Nn是递减数列.容易计算813,811,1,214321SSSS，57,2029,1523,10174321TTTT显然11TS，22TS，33TS，44TS所以当3n时，nnTS；当3n时，nnTS.8、解：设第一次复习后的存留量与不复习的存留量之差为，由题意知，所以当时，≤，当且仅当时取等号，所以“二次复习最佳时机点”为第14天．(2)≤，当且仅当时取等号，由题意，所以．45