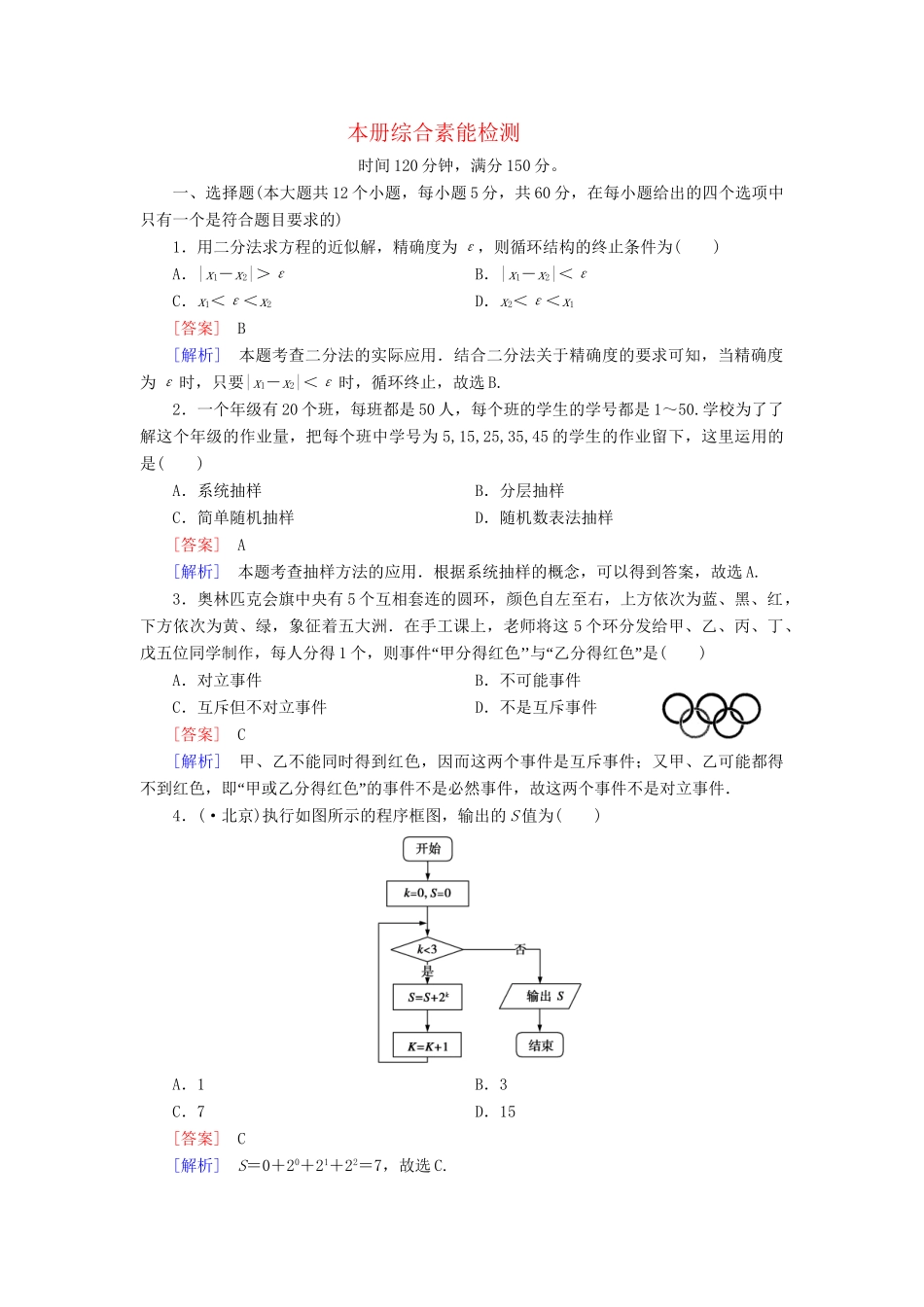
本册综合素能检测时间120分钟,满分150分。一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.用二分法求方程的近似解,精确度为ε,则循环结构的终止条件为()A.|x1-x2|>εB.|x1-x2|<εC.x1<ε<x2D.x2<ε<x1[答案]B[解析]本题考查二分法的实际应用.结合二分法关于精确度的要求可知,当精确度为ε时,只要|x1-x2|<ε时,循环终止,故选B.2.一个年级有20个班,每班都是50人,每个班的学生的学号都是1~50.学校为了了解这个年级的作业量,把每个班中学号为5,15,25,35,45的学生的作业留下,这里运用的是()A.系统抽样B.分层抽样C.简单随机抽样D.随机数表法抽样[答案]A[解析]本题考查抽样方法的应用.根据系统抽样的概念,可以得到答案,故选A.3.奥林匹克会旗中央有5个互相套连的圆环,颜色自左至右,上方依次为蓝、黑、红,下方依次为黄、绿,象征着五大洲.在手工课上,老师将这5个环分发给甲、乙、丙、丁、戊五位同学制作,每人分得1“’’“”个,则事件甲分得红色与乙分得红色是()A.对立事件B.不可能事件C.互斥但不对立事件D.不是互斥事件[答案]C[解析]甲、乙不能同时得到红色,因而这两个事件是互斥事件;又甲、乙可能都得“”不到红色,即甲或乙分得红色的事件不是必然事件,故这两个事件不是对立事件.4.(·北京)执行如图所示的程序框图,输出的S值为()A.1B.3C.7D.15[答案]C[解析]S=0+20+21+22=7,故选C.5.如图所示是一容量为100的样本的频率分布直方图,则由图形中的数据,样本落在[15,20]内的频数为()A.20B.30C.40D.50[答案]B[解析]样本落在[15,20]内的频率是1-5×(0.04+0.1)=0.3,则样本落在[15,20]内的频数为0.3×100=30.6.(·浙江)在3张奖卷中有一、二等奖各1张,另一张无奖,甲、乙两人各抽取1张,两人都中奖的概率是()A.B.C.D.[答案]B[解析]设三张卷分别用A,B,C代替,A一等奖;B二等奖;C无奖,甲、乙各抽一张共包括(A,B),(A,C),(B,A),(B,C),(C,A),(C,B)6种基本事件,其中甲、乙都中奖包括两种,P==,故选B.7.某中学高三年级从甲、乙两个班级中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则x+y的值为()A.7B.8C.9D.10[答案]B[解析] 85×7=2×70+3×80+2×90+30+x,∴x=5.又 乙班学生成绩的中位数是83,∴y=3,∴x+y=5+3=8,故选B.8.计算机常用的十六进制是适十六进一,采用数字0~9和字母A~F共16个计算符号,这些符号与十进制数的对应关系如下表:十六进制0123456789ABCDEF十进制0123456789101112131415例如:用十六进制表示E+D=1B,则A×B=()A.6EB.72C.5FD.5B[答案]A[解析]本题考查进位制间的相互转化.用十进制表示A×B=10×11=110,而110=6×16+14=6E(16),故选A.9.如果数据x1,x2…,,xn的平均数为,方差为s2,则5x1+2,5x2+2…,,5xn+2的平均数和方差分别为()A.,s2B.5+2,s2C.5+2,25s2D.,25s2[答案]C[解析]本题考查平均数与方差的计算公式.由平均数与方差的计算公式分析可得5x1+2,5x2+2…,,5xn+2的平均数为5+2,方差为25s2,故选C.10.扇形AOB的半径为1,圆心角为90°.点C、D、E将弧AB等分成四份.连接OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰为的概率是()A.B.C.D.[答案]A[命题立意]本题考查扇形面积公式及古典概型概率求解,难度中等.[解析]据题意若扇形面积为,据扇形面积公式=×α×1⇒α=,即只需扇形中心角为即可,列举可得这种情况共有3种,而整个基本事件个数共有10种,故其概率为.11.(~·石家庄模拟)从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:身高x(cm)160165170175180体重y(kg)6366707274根据上表可得回归直线方程y=0.56x+a,据此模型预报身高为172cm的高三男生的体重为()A.70.09B.70.12C.70.55D.71.05[答案]B[解析]由表中数据得==170,==69.将(,)代入y=0.56x+a,∴69=0.56×170+a,∴a=-26.2,∴y=0.56x-26.2.∴当x=172时,y=70....