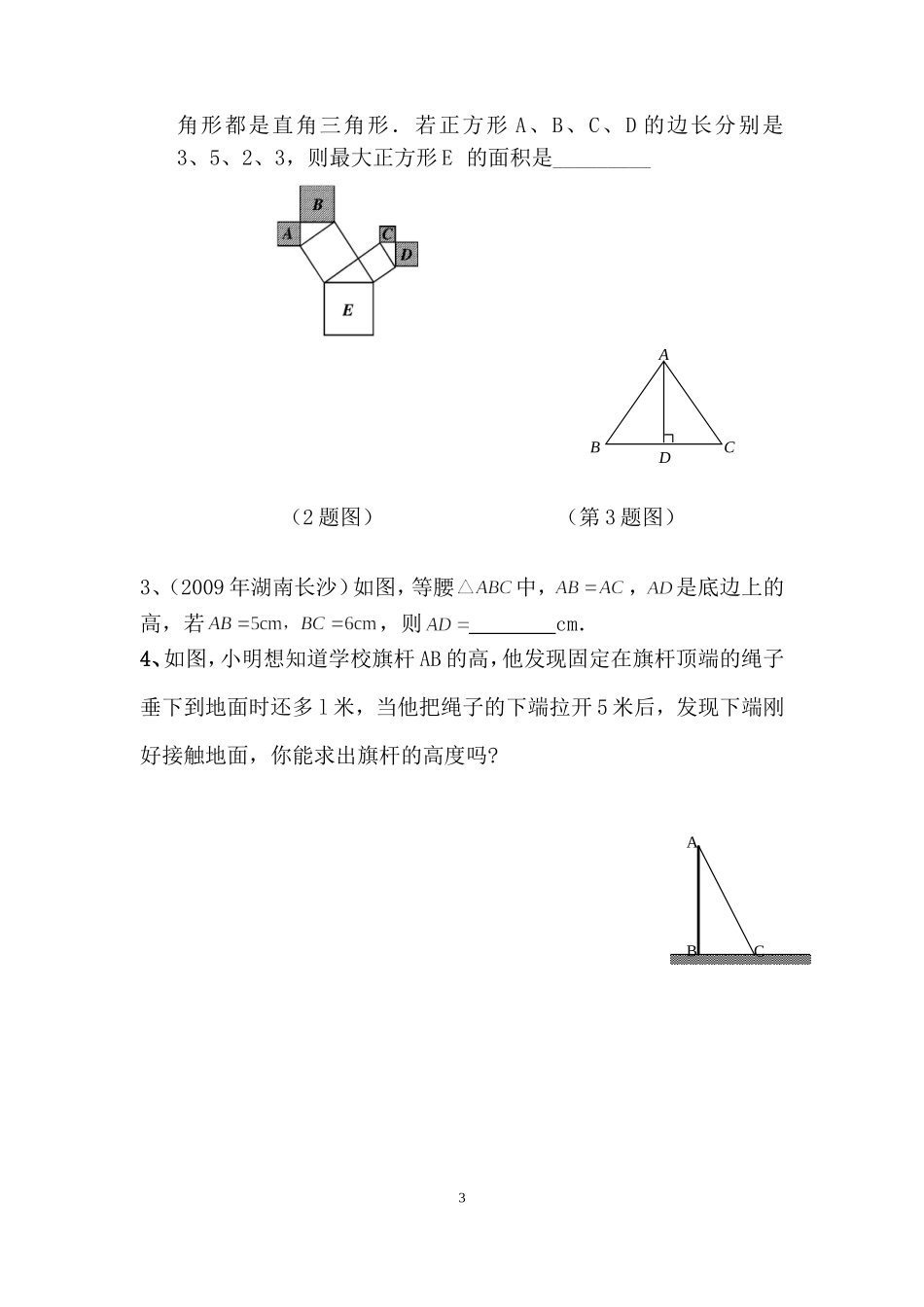
勾股定理期末复习(一)初二()班姓名_____第组学习目标:复习勾股定理及其逆定理,能利用它们求三角形的边长或证明三角形是直角三角形.专题一:勾股定理1.勾股定理:若直角三角形的三边分别为,,,,则有:。公式变形①:若知道,,则;公式变形②:若知道,,则;公式变形③:若知道,,则;例1:求图中的直角三角形中未知边的长度:,.(1)在Rt中,若,,,则.(2)在Rt中,若,a=6,b=10,则.(3)在Rt中,若,,,则.3、在Rt△ABC,∠C=90°,c=25,a:b=3:4,则a=,b=。例题2、已知直角三角形的两边长分别为5和12,求第三边。1915b1024c练习:已知直角三角形的两边长分别为3cm和5cm,,则第三边长为。例题3已知:等边△ABC的边长是6。求:(1)等边△ABC的高。⑵S△ABC。例题4一个直角三角形的周长为9,斜边为4,求这个三角形的面积。练习:1.直角三角形两直角边长分别为5和12,则它斜边上的高为_______.2、图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三2角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是_________(2题图)(第3题图)3、(2009年湖南长沙)如图,等腰中,,是底边上的高,若,则cm.4、如图,小明想知道学校旗杆AB的高,他发现固定在旗杆顶端的绳子垂下到地面时还多l米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能求出旗杆的高度吗?[3ACDBABC5、如图,在直角三角形中,AC=18,BC=24,现将AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求BD的长。勾股定理期末复习(二)初二()班姓名_____第组学习目标:复习勾股定理及其逆定理,能利用它们求三角形的边长或证明三角形是直角三角形.学习过程:专题二:勾股定理的逆定理例1:下列2组数据为一个三角形的边长:(1)5、12、13(2)4、5、6找出哪组能够构成直角三角形,并说明理由。解:(1)(2)4练习:1、在下列长度的各组线段中,能组成直角三角形的是()A.12,15,17B.9,16,25C.5a,12a,13a(a>0)D.2,3,42.若△ABC的三边abc,满足(a-b)(a2+b2-c2)=0,则△ABC是()A.等腰三角形;B.直角三角形;C.等腰三角形或直角三角形;D.等腰直角三角形。3、在△ABC中,若a2=b2-c2,则△ABC是三角形,是直角;4、如图,AD⊥BC,垂足为D,如果CD=1,AD=2,BD=4,试判断ΔABC的形状,并说明理由。专题三:勾股定理的应用例题1、求下列阴影部分的面积:(1)阴影部分是正方形;(2)阴影部分是长方形;(3)阴影部分是半圆.5DCBAS=S=S=练习:若的三条边长分别为3cm、4cm、5cm。则_______例题2、如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为米。练习:1、如图,从电线杆离地面6m处向地面拉一条长10m的固定缆绳,这条缆绳在地面的固定点距离电线杆底部有m.2、如图,某人欲横渡一条河,由于水流的影响,实际上岸地点C偏离欲到达点B200m,结果他在水中实际游了520m,求该河流的宽度为_________。思维拓展:3、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.(1)求DC的长;(2)求AB的长;(3)求证:△ABC是直角三角形.3、已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。6CABD图4ABCDEDCBANOMAMONB来源:学科网]4、如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米。①求梯子顶端与地面的距离OA的长。②若梯子顶点A下滑1米到C点,求梯子的底端向右滑到D的距离。7