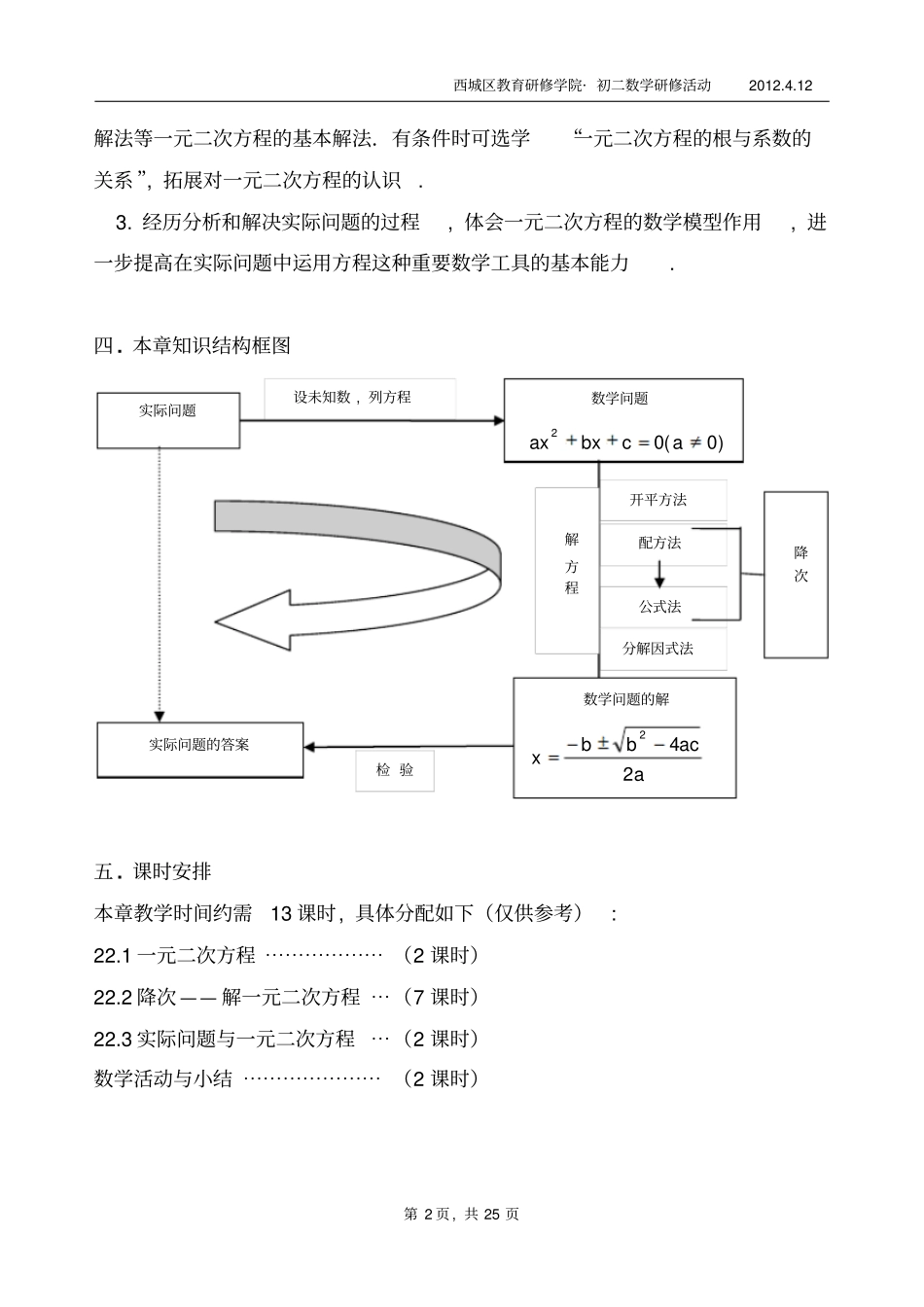
西城区教育研修学院·初二数学研修活动2012.4.12第1页,共25页第二十二章《一元二次方程》教材分析北京八中刘颖一.本章的主要内容:1.主要内容:一元二次方程及其有关概念,一元二次方程的解法(配方法、公式法、因式分解法),运用一元二次方程分析和实际问题.2.本章重点:一元二次方程的解法,难点:一元二次方程的应用.二.中考考试要求:(2012年)考试内容考试要求ABC一元二次方程了解一元二次方程的概念,理解配方法,会用直接开平方法、配方法、公式法、因式分解法解简单的数字系数的一元二次方程,理解各种解法的依据能由一元二次方程的概念确定二次项系数中所含字母的取值范围;能选择适当的方法解一元二次方程;会用一元二次方程根的判别式判断根的情况能利用根的判别式说明含有字母系数的一元二次方程根的情况及由方程根的情况确定方程中待定系数的取值范围;会运用一元二次方程解决简单的实际问题三.课程学习目标1.以分析实际问题中的等量关系并求解其中的未知数为背景,认识一元二次方程及其有关概念.2.根据化归的思想,抓住“降次”这一基本策略,掌握配方法、公式法和因式分西城区教育研修学院·初二数学研修活动2012.4.12第2页,共25页解法等一元二次方程的基本解法.有条件时可选学“一元二次方程的根与系数的关系”,拓展对一元二次方程的认识.3.经历分析和解决实际问题的过程,体会一元二次方程的数学模型作用,进一步提高在实际问题中运用方程这种重要数学工具的基本能力.四.本章知识结构框图五.课时安排本章教学时间约需13课时,具体分配如下(仅供参考):22.1一元二次方程⋯⋯⋯⋯⋯⋯(2课时)22.2降次——解一元二次方程⋯(7课时)22.3实际问题与一元二次方程⋯(2课时)数学活动与小结⋯⋯⋯⋯⋯⋯⋯(2课时)实际问题数学问题)0(02acbxax设未知数,列方程实际问题的答案数学问题的解aacbbx242解方程开平方法配方法公式法分解因式法检验降次西城区教育研修学院·初二数学研修活动2012.4.12第3页,共25页六.内容安排22.1节以实际问题为背景,引出一元二次方程的概念,归纳出一元二次方程的一般形式,给出一元二次方程的根的概念,并提出一元二次方程的根会出现不唯一的情况.这些概念是全章后续内容的基础.22.2节讨论一元二次方程的基本解法,其中包括直接开平方法、配方法、公式法和因式分解法等,这一节是全章的重点内容之一.在本章之前的方程都是一次方程或可化为一次方程的分式方程,一元二次方程是首次出现的高于一次的方程.解二次方程的基本策略是将其转化为一次方程,这就是“降次”.本节首先通过解比较简单的一元二次方程,引导学生认识直接开平方法解方程;然后讨论比较复杂的一元二次方程,通过对比一边为完全平方形式的方程,使学生认识配方法的基本原理并掌握其具体方法;有了配方法作基础,再讨论如何用配方法解一元二次方程的一般形式20axbxc(0a),就得到一元二次方程的求根公式,于是有了直接利用公式的公式法,并引出用判别式确定一元二次方程的根的情况.本节在公式法后讨论因式分解法解一元二次方程,这种解法要使方程的一边为两个一次因式相乘,另一边为0,再分别令每个一次因式为0.这几种解法都是依降次的思想,将二次方程转化为一次方程,只是具体的降次手段有所不同.本节最后增加了选学内容“一元二次方程的根与系数的关系”.学习这一内容可以进一步加深对一元二次方程及其根的认识,为以后的学习做准备.22.3节安排了3个探究内容,结合实际问题,分别讨论传播问题、增长率问题和几何图形面积问题.一元二次方程与许多实际问题都有联系,本节不是按照实际问题的类型分类和选材的,而是选取几个具有一定代表性的实际问题来进一步讨论如何建立和利用方程模型,重点在分析实际问题中的数量关系并以方程形式进行表示,这种数学建模思想的体现与前面有关方程的各章是一致的,只是在问题中数量关系的复杂程度上又有新的发展,数学模型由一次方程或可西城区教育研修学院·初二数学研修活动2012.4.12第4页,共25页以化为一次方程的分式方程变为一元二次方程.本章从引言到小结始终保持贴近实际、贴近生活.这样安排主要目的是:1.反映客观世界与数学的密切联系;2.加强对应用数学知识分析和解决实际问题的意...