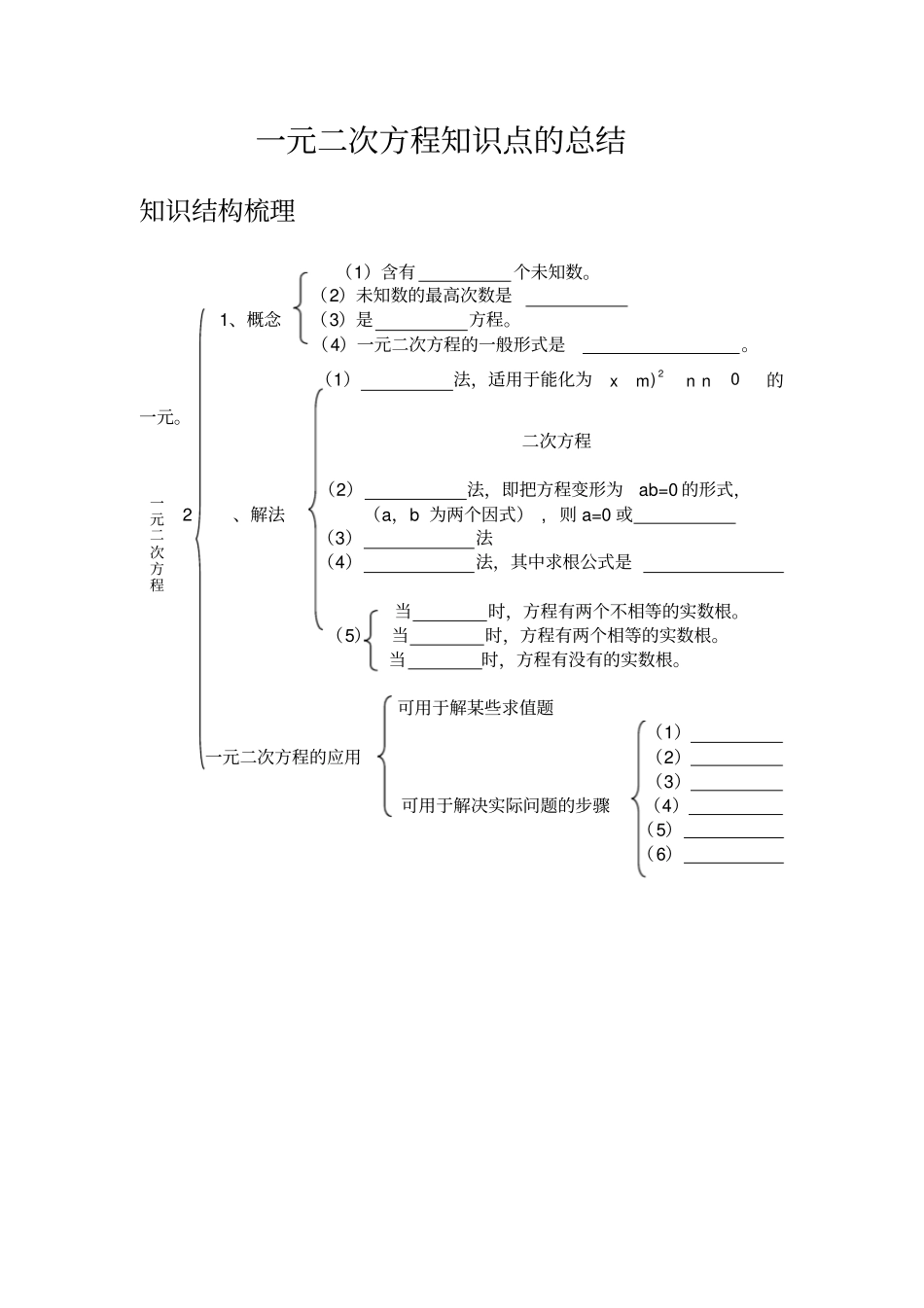
一元二次方程知识点的总结知识结构梳理(1)含有个未知数。(2)未知数的最高次数是1、概念(3)是方程。(4)一元二次方程的一般形式是。(1)法,适用于能化为0)2nnmx的一元。二次方程(2)法,即把方程变形为ab=0的形式,2、解法(a,b为两个因式),则a=0或(3)法(4)法,其中求根公式是当时,方程有两个不相等的实数根。(5)当时,方程有两个相等的实数根。当时,方程有没有的实数根。可用于解某些求值题(1)一元二次方程的应用(2)(3)可用于解决实际问题的步骤(4)(5)(6)一元二次方程知识点归类建立一元二次方程模型知识点一一元二次方程的定义如果一个方程通过移项可以使右边为0,而左边只含有一个未知数的二次多项式,那么这样的方程叫做一元二次方程。注意:一元二次方程必须同时满足以下三点:①方程是整式方程。②它只含有一个未知数。③未知数的最高次数是2.同时还要注意在判断时,需将方程化成一般形式。例下列关于x的方程,哪些是一元二次方程?⑴3522x;⑵062xx;(3)5xx;(4)02x;(5)12)3(22xxx知识点二一元二次方程的一般形式一元二次方程的一般形式为02cbxax(a,b,c是已知数,0a)。其中a,b,c分别叫做二次项系数、一次项系数、常数项。注意:(1)二次项、二次项系数、一次项、一次项系数,常数项都包括它前面的符号。(2)要准确找出一个一元二次方程的二次项系数、一次项系数和常数项,必须把它先化为一般形式。(3)形如02cbxax不一定是一元二次方程,当且仅当0a时是一元二次方程。例1将下列方程化为一般形式,并分别指出它们的二次项系数、一次项系数和常数项。(1)xx2752;(2)832xx;(3)22343xxx例2已知关于x的方程021122xmxmm是一元二次方程时,则m知识点三一元二次方程的解使方程左、右两边相等的未知数的值叫做方程的解,如:当2x时,0232xx所以2x是0232xx方程的解。一元二次方程的解也叫一元二次方程的根。知识点四建立一元二次方程模型建立一元二次方程模型的步骤是:审题、设未知数、列方程。注意:(1)审题过程是找出已知量、未知量及等量关系;(2)设未知数要带单位;(3)建立一元二次方程模型的关键是依题意找出等量关系。例如图(1),有一个面积为150㎡的长方形鸡场,鸡场一边靠墙(墙长18m),另三边用竹篱笆围成,若竹篱笆的长为35m,求鸡场的长和宽各为多少?鸡场(只设未知数,列出方程,并将它化成一般形式。)因式分解法、直接开平方法知识点一因式分解法解一元二次方程如果两个因式的积等于0,那么这两个方程中至少有一个等于0,即若pq=0时,则p=0或q=0。用因式分解法解一元二次方程的一般步骤:(1)将方程的右边化为0;(2)将方程左边分解成两个一次因式的乘积。(3)令每个因式分别为0,得两个一元一次方程。(4)解这两个一元一次方程,它们的解就是原方程的解。关键点:(1)要将方程右边化为0;(2)熟练掌握多项式因式分解的方法,常用方法有:提公式法,公式法(平方差公式,完全平方公式)等。例用因式分解法解下列方程:(1)xx452;(2)025)32(2x;(3)222596xxx。知识点二直接开平方法解一元二次方程若02aax,则x叫做a的平方根,表示为ax,这种解一元二次方程的方法叫做直接开平方法。(1)02aax的解是ax;(2)02nnmx的解是mnx;(3)0,02cmcnmx且的解是mncx。例用直接开平方法解下列一元二次方程(1)01692x;(2)01652x;(3)22135xx知识点三灵活运用因式分解法和直接开平方法解一元二次方程形如002kkbax的方程,既可用因式分解法分解,也可用直接开平方法解。例运用因式分解法和直接开平方法解下列一元二次方程。(1)036542x;(2)03212x知识点四用提公因式法解一元二次方程把方程左边的多项式(方程右边为0时)的公因式提出,将多项式写出因式的乘积形式,然后利用“若pq=0时,则p=0或q=0”来解一元二次方程的方法,称为提公因式法。如:0201.02tt,将原方程变形为0201.0tt,由此可得出200,0020.0021tttt,即或注意:在解方程时,千万注意不能把方程两边都同时除以一个含有未知数的式子,否则可能丢失原方程的根。知识点五形如“为常数babxbax,02”的方程的解法。对于形如“为常数b...