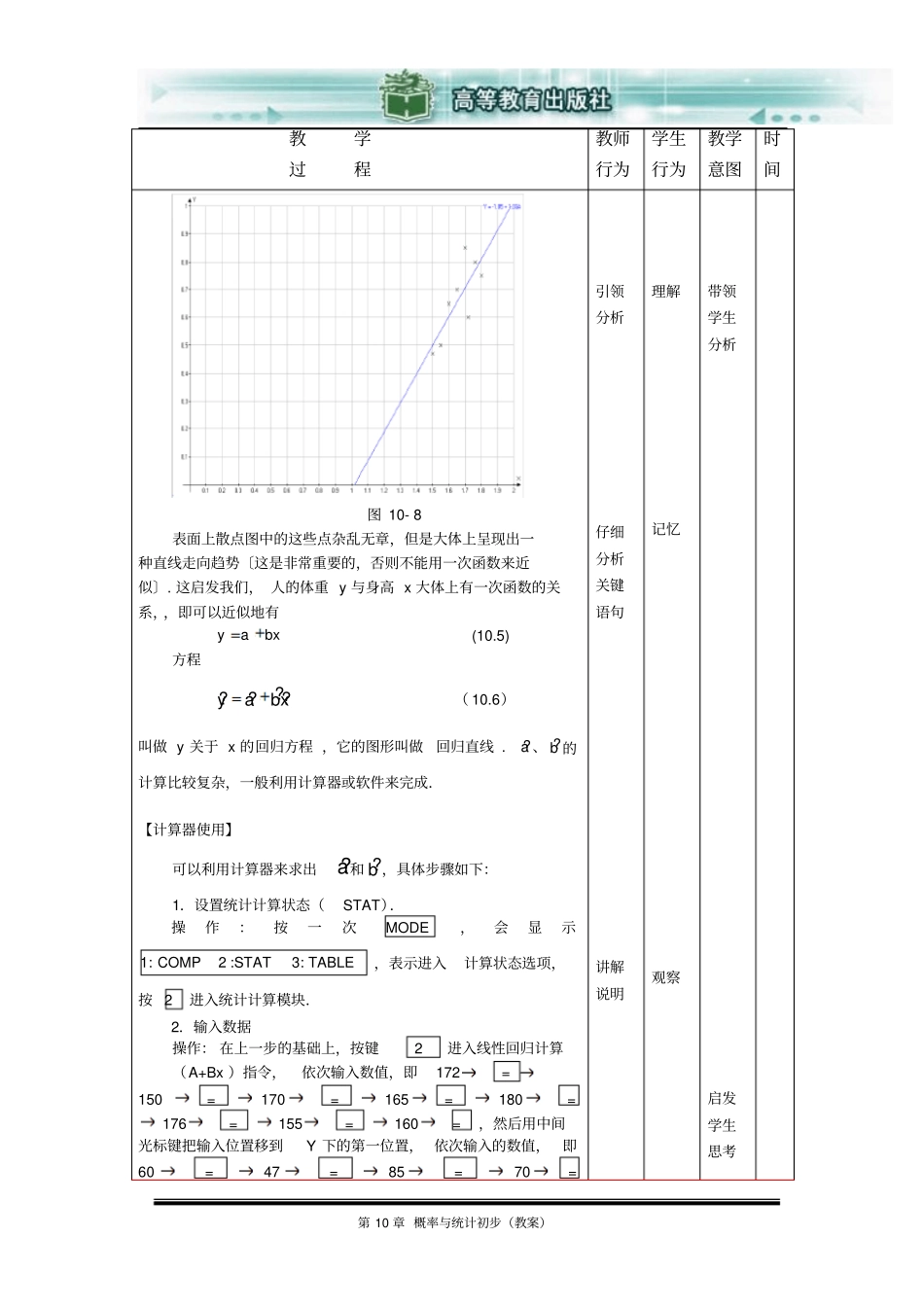
第10章概率与统计初步(教案)【课题】10.5一元线性回归【教学目标】知识目标:(1)了解相关关系的概念.(2)了解一元线性回归思想及回归方程的建立.能力目标:能根据数据利用软件建立一元线性回归方程,从而增强学生的数据处理技能及计算工具使用技能.情感目标:(1)尝试应用计算软件或计算器建立回归方程的过程,感受计算工具带来的便捷.(2)关注生活中的数学模型,体会数学知识的应用.【教学重点】一元回归方程.【教学难点】理解相关关系、回归分析概念.【教学设计】一切自然现象和社会现象都不是孤立的.事物与事物之间,变量与变量之间,都存在着某种关系.这类关系大体可分为两类:一类是确定性的,另一类是非确定性的.用来近似地描述具有统计相关关系的变量之间关系的函数叫做回归函数.一元回归处理两个变量之间的相关关系问题.如果两个变量之间的相关关系是线性的,就是一元线性回归问题.本教材根据学生的实际情况只介绍两个变量间的一元线性回归问题.通过建立回归方程,可以对相应的变量进行预测和控制.回归分析具有广泛的应用.在本节教学过程中,由于统计量的计算十分繁杂,因此,必须注重训练学生利用计算器或计算机软件进行计算、求解的能力.【教学备品】教学课件.【课时安排】2课时.(90分钟)【教学过程】第10章概率与统计初步(教案)教学过程教师行为学生行为教学意图时间*揭示课题10.5一元线性回归*创设情境兴趣导入【问题】人的身高(cm)与体重(kg)之间有没有联系呢?也许有人知道,平均标准体重的数值约为体重≈身高-105.这个结果是通过大量样本的分析,估算出来的.介绍质疑讲解说明了解思考启发学生思考05*动脑思考探索新知【新知识】表10-12中是随机抽取的8个学生的身高(单位:cm)与体重(单位:kg)的数据:表10-12编号12345678身高x172150170165180176155160体重y6047857075805065学生的身高与体重之间存在着一定的关系,这种关系不像以前研究的函数关系那样,知道身高,就能确定体重的值.但是一般身高的人,体重还是比较大的.变量之间的这种非确定性的相互依存的关系叫做相关关系.它的特点是,当一个变量或n个变量的值确定后,另一个变量的值虽然与它(或它们)有着密切的关系,但却无法完全确定.下面要研究的问题是,能否利用确定性的关系来近似的描述相关关系.讲解说明引领分析理解记忆带领学生分析15*运用知识强化练习请举出具有相关关系变量的实例.提问回答20*动脑思考探索新知【新知识】我们继续研究8个学生的身高与体重的关系.建立平面直角坐标系oxy,x轴表示身高(单位:cm),y轴表示体重(单位:kg).上述样本中每位学生的身高与体重组成的有序数对(,)xy,对应于平面上一个点,这些点组成的图形叫做散点图.如图10-8所示.讲解说明思考第10章概率与统计初步(教案)教学过程教师行为学生行为教学意图时间图10-8表面上散点图中的这些点杂乱无章,但是大体上呈现出一种直线走向趋势〔这是非常重要的,否则不能用一次函数来近似〕.这启发我们,人的体重y与身高x大体上有一次函数的关系,,即可以近似地有yabx(10.5)方程????yabx(10.6)叫做y关于x的回归方程,它的图形叫做回归直线.?a、?b的计算比较复杂,一般利用计算器或软件来完成.【计算器使用】可以利用计算器来求出a?和b?,具体步骤如下:1.设置统计计算状态(STAT).操作:按一次MODE,会显示1:COMP2:STAT3:TABLE,表示进入计算状态选项,按2进入统计计算模块.2.输入数据操作:在上一步的基础上,按键2进入线性回归计算(A+Bx)指令,依次输入数值,即172=150=170=165=180=176=155=160=,然后用中间光标键把输入位置移到Y下的第一位置,依次输入的数值,即60=47=85=70=引领分析仔细分析关键语句讲解说明理解记忆观察带领学生分析启发学生思考第10章概率与统计初步(教案)教学过程教师行为学生行为教学意图时间75=80=50=65AC.在输入中注意x的量和y的量要对应起来.3.显示计算结果(1)按键SHIFT1,然后按键5,最后依次按键1=,显示回归系数:105A.(2)按键SHIFT1,然后按键5,最后依次按键2=,显示回归系数:1.02B.因此,身高与体重之间的关系的线性回归方程为1....