正弦余弦曲线VIP免费

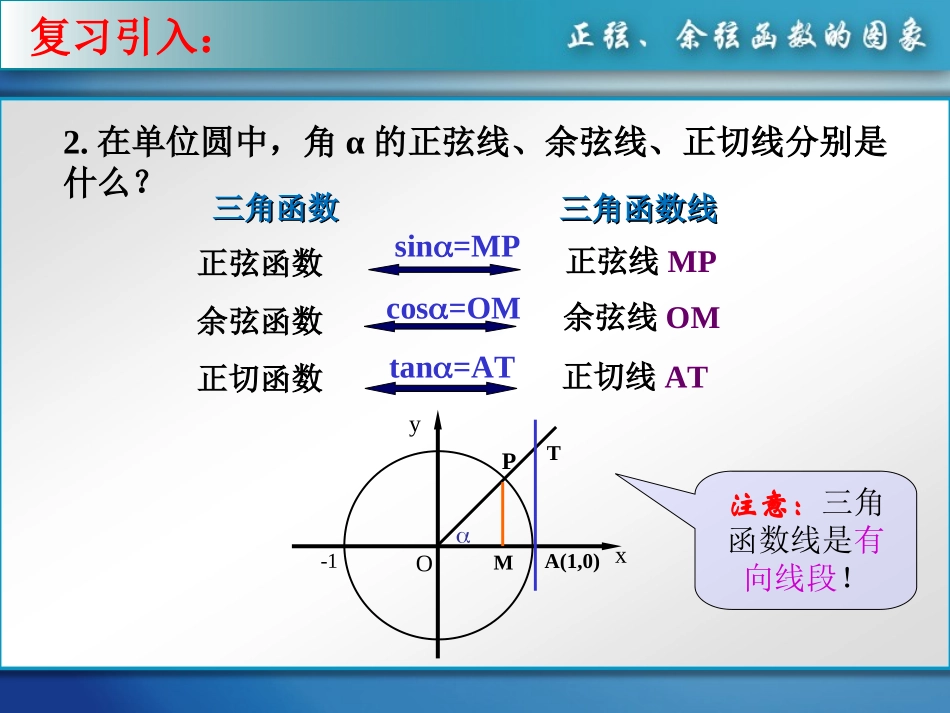
1.我们知道，实数集与角的集合之间可以建立一一对应关系，而一个确定的角又对应唯一确定的正弦（或余弦）值。任意给定一个实数x，有唯一确定的值sinx（或cosx）与之对应。由这个对应法则所确定的函数y=sinx（或y=cosx）叫做正弦函数（或余弦函数），其定义域都是R。复习引入：三角函数三角函数三角函数线三角函数线正弦函数余弦函数正切函数正切线AT2.在单位圆中，角α的正弦线、余弦线、正切线分别是什么？yxO-1PMA(1,0)Tsin=MPcos=OMtan=AT注意：三角函数线是有向线段！正弦线MP余弦线OM复习引入：复习引入：3.遇到一个新的函数，我们往往要研究函数的哪些问题？一个函数总具有许多基本性质，要直观、全面了解函数的基本特性，我们一般从函数的图像入手。复习引入：?)3πsin,3πC(如何在直角坐标系中作出点OP1O3πMxy3π)3πsin,3πC(.几何描点23.2π2π(,sin)33思考1：能否借助上面作点C的方法，在直角坐标系中作出正弦函数sin,0,2yxx的图象呢？思考2：解决办法：利用单位圆中正弦线来解决O1Oyx33234352-11描图：用光滑曲线将这些正弦线的终点连结起来AB探究新知探究新知y=sinxx[0,2]终边相同角的三角函数值相等即：sin(x+2k)=sinx,kZ利用图象平移y=sinxxR问题：如何作出的图象？y=sinx，xR探究新知探究新知x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线x6yo--12345-2-3-41探究新知x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同探究新知yxo1-122322如何作出正弦函数的图象（在精确度要求不太高时）？(0,0)(,1)2(,0)(,-1)23(2,0)五点法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)最高点最低点与x轴的交点探究新知xsinx22302练习1:用五点法作出函数y=sinx，x[0,2]的简图：o1yx22322-12y=sinx，x[0,2]100-10步骤：1.列表2.描点3.连线精讲精练x6yo--12345-2-3-41(0,1)(,0)2(,-1)(,0)23(2,1)22321-1xyoxcosx2322001-101练习2:用五点法作y=cosx,x[∈0,2π]的简图步骤：1.列表2.描点3.连线例1画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线例2画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]练习3：（1）作函数y=1+3cosx，x[0,2π]∈的简图(２)作函数y=2sinx-1，x[0,2π]∈的简图（1）yx小结1.正弦曲线、余弦曲线几何画法五点法2.注意与诱导公式、三角函数线等知识的联系yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]3.正、余弦函数的图象每相隔2π个单位重复出现，因此，只要记住它们在[0，2π]内的图象形态，就可以画出正弦曲线和余弦曲线.4.作与正、余弦函数有关的函数图象，是解题的基本要求，用“五点法”作图是常用的方法.思想方法：1.数形结合思想2.转化与化归思想作业：1.活页练习课时作业六2.课后请同学们利用三角函数线（把单位圆8等分）来作出正弦函数图象？例1画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线例2画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]练习：（1）作函数y=1+3cosx，x[0,2π]∈的简图(２)作函数y=2sinx-1，x[0,2π]∈的简图（1）yx正弦...