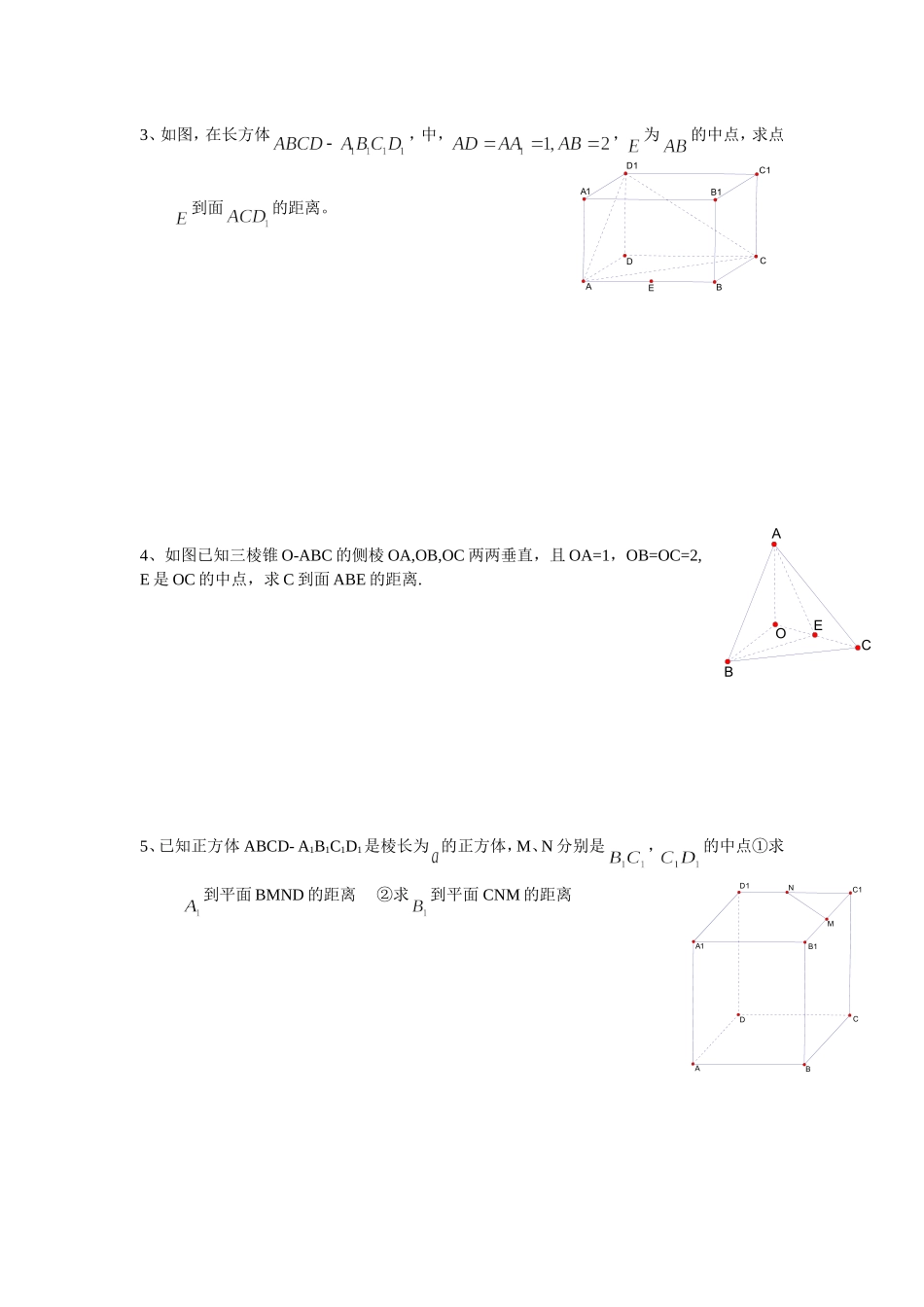
等体积法求点到平面距离用等体积法求点到平面的距离主要是一个转换的思想,即要将所要求的垂线段置于一个四面体中,其中四面体的一个顶点为所给点,另外三点位于所给点射影平面上,这里不妨将射影平面上的三点构成的三角形称为底面三角形。先用简单的方法求出四面体的体积,然后计算出底面三角形的面积,再根据四面体体积公式求出点到平面的距离。在常规方法不能轻松获得结果的情况下,如果能用到等体积法则可以很大程度上提高解题效率,达到事半功倍的效果。特别是遇到四面体的有一条棱垂直于其所相对的底面时,首选此方法。下面用等体积法求解例子.例:所示的正方体棱长为,求点到平面的距离解法(等体积法):如图所示,作垂直于平面于点,则长度为所求。对于四面体,易见底面的高为,底面的高为。对四面体的体积而言有:即有:,也即:由,从而为正三角形,,进而可求得又易计算得到的面积为所以从上面的解答过程知道,我们在使用等体积法求点到平面距离时使用的点与平面间的垂线段只是概念上的,并不一定要知道点在平面射影的具体位置,从而也就不需要使用几何方法寻找或者求作垂线段,垂线段的长度在这种方法上只是作为几何体高的意义而存在的。练习:1、如图所示,棱长均为a的正三棱柱中,D为AB中点,连结A1D,DC,A1C.(1)求BC1到面A1DC的距离.2、如图所示,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.求点C到平面APB的距离.3、如图,在长方体,中,,为的中点,求点到面的距离。4、如图已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点,求C到面ABE的距离.5、已知正方体ABCD-A1B1C1D1是棱长为的正方体,M、N分别是,的中点①求到平面BMND的距离②求到平面CNM的距离DCBAB1D1C1A1EAOBCEDCBAB1D1C1A1NM