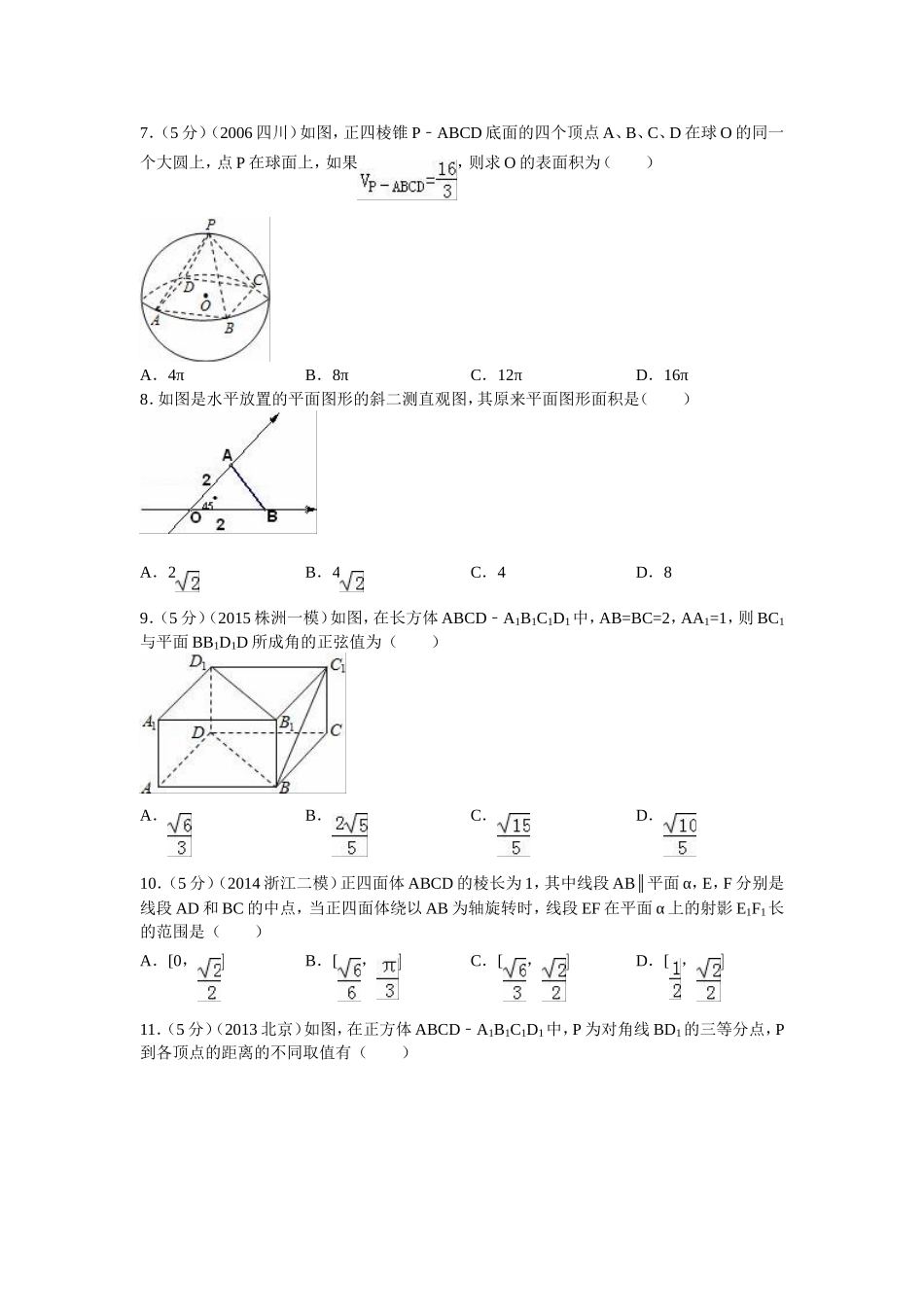
2015-2016学年河北省衡水中学高一(下)期中数学试卷(理科)一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知向量,则与的夹角为()A.0°B.45°C.90°D.180°2.如图,正方体ABCDA﹣1B1C1D1中,棱长为1,PB=PB′,则P点坐标为()A.(,)B.(,,)C.(,,)D.(,,)3.设A(3,3,1)、B(1,0,5)、C(0,1,0),则AB的中点M到C点的距离为()A.B.C.D.4.设m,n是不同的直线,α、β、γ是三个不同的平面,有以下四个命题:①若mα⊥,nα⊥,则mn∥;②若α∩γ=m,β∩γ=n,mn∥则αβ∥;③若αβ∥,βγ∥,mα⊥,则mγ⊥④若γα⊥,γβ⊥,则αβ∥.其中正确命题的序号是()A.①③B.②③C.③④D.①④5.正四棱锥的侧棱长是底面长的k倍,则k的取值范围是()A.(0,+∞)B.(,+∞})C.(,+∞)D.(,+∞)6.(5分)(2013新郑市校级模拟)已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是()A.πR2B.πR2C.πR2D.πR27.(5分)(2006四川)如图,正四棱锥PABCD﹣底面的四个顶点A、B、C、D在球O的同一个大圆上,点P在球面上,如果,则求O的表面积为()A.4πB.8πC.12πD.16π8.如图是水平放置的平面图形的斜二测直观图,其原来平面图形面积是()A.2B.4C.4D.89.(5分)(2015株洲一模)如图,在长方体ABCDA﹣1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为()A.B.C.D.10.(5分)(2014浙江二模)正四面体ABCD的棱长为1,其中线段AB∥平面α,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面α上的射影E1F1长的范围是()A.[0,]B.[,]C.[,]D.[,]11.(5分)(2013北京)如图,在正方体ABCDA﹣1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有()A.3个B.4个C.5个D.6个12.(5分)(2011怀柔区一模)已知三棱锥ABCO﹣,OA、OB、OC两两垂直且长度均为6,长为2的线段MN的一个端点M在棱OA上运动,另一个端点N在△BCO内运动(含边界),则MN的中点P的轨迹与三棱锥的面所围成的几何体的体积为()A.B.或36+C.36﹣D.或36﹣二.填空题(本大题共4个小题,每小题5分,共20分.)13.已知长方体ABCDA﹣1B1C1D1,设=,=,=,E,F分别为AA1,C1D1中点,则可用表示为.14.如图,四棱锥PABCD﹣中,∠BAD=ABC=90°∠,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为.15.(5分)(2014德州二模)一个几何体的三视图如图所示,其侧(左)视图是一个等边三角形,则这个几何体的体积是.16.如图,正方体ABCDA﹣1B1C1D1的棱长为1,E为A1B1的中点,则下列五个命题:①点E到平面ABC1D1的距离为;②直线BC与平面ABC1D1所成角为45°;③空间四边形ABCD1在正方体六个面内的射影围成的图形中,面积最小的值为;BE④与CD1所成角的正弦值为;⑤二面角ABD﹣1C﹣的大小为.其中真命题是.(写出所有真命题的序号)三.解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(10分)(2014黄浦区二模)(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示.(1)求圆柱体的侧面积S侧的值;(2)若C1是半圆弧A1B1的中点,点C在半径OA上,且OC=OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.18.(12分)(2012秋台州期中)如图四边形ABCD为梯形,ADBC∥,∠ABC=90°,求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.19.(12分)(2014湖北模拟)如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=,点F是PB的中点,点E在边BC上移动.(Ⅰ)若PA=1,求证:AFPC⊥;(Ⅱ)若二面角PBCA﹣﹣的大小为60°,则CE为何值时,三棱锥FACE﹣的体积为?20.(12分)(2014春凉州区校级期末)如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,ACBC⊥,且AC=BC.(1)求证:AM⊥平面EBC;(2)求二面角AEBC﹣...