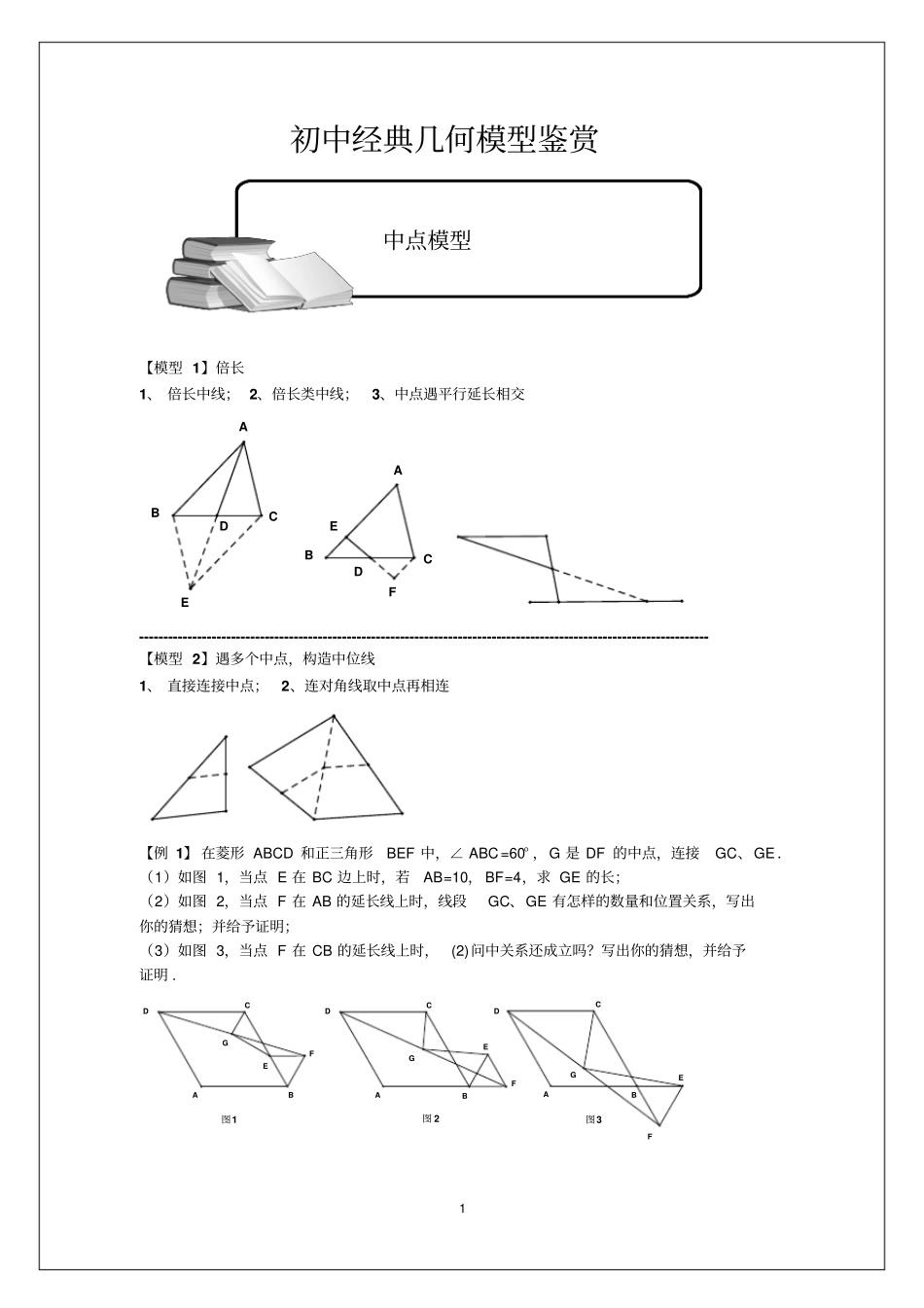
1初中经典几何模型鉴赏【模型1】倍长1、倍长中线;2、倍长类中线;3、中点遇平行延长相交----------------------------------------------------------------------------------------------------------------------【模型2】遇多个中点,构造中位线1、直接连接中点;2、连对角线取中点再相连【例1】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF的中点,连接GC、GE.(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;(2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的数量和位置关系,写出你的猜想;并给予证明;(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.EDABCFDABCE图3图2图1GFDCGFDCGFDCABEEBAEBA中点模型2【例2】如图,在菱形ABCD中,点E、F分别是BC、CD上一点,连接DE、EF,且AE=AF,BAFDAE.(1)求证:CE=CF;(2)若120ABC,点G是线段AF的中点,连接DG,EG.求证:DG上GE.【例3】如图,在四边形ABCD中,AB=CD,E、F分别为BC、AD中点,BA交EF延长线于G,CD交EF于H.求证:∠BGE=∠CHE.【模型1】构造轴对称【模型2】角平分线遇平行构造等腰三角形----------------------------------------------------------------------------------------------------------------------HGEFABDC角平分线模型3EABCODEABCODBOAC【例4】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为.【条件】OAOBOCODAOBCOD,,【结论】OACOBD;AEBOABCOD(即都是旋转角);OEAED平分;----------------------------------------------------------------------------------------------------------------------【例5】如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为F,连接OF,则OF的长为.HGFEADBC导角核心图形:八字形手拉手模型4FEBDAC【例6】如图,ABC中,90BAC,AB=AC,AD⊥BC于点D,点E在AC边上,连结BE,AG⊥BE于F,交BC于点G,求DFG【例7】如图,在边长为62的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG于点H,交AD于点F,连接CE、BH。若BH=8,则FG=.【模型1】【条件】如图,四边形ABCD中,AB=AD,180BADBCDABCADC【结论】AC平分BCDGFDCBAEEBDAC邻边相等对角互补模型5CDABEFECDBAFEGCDABGFECDBA【模型2】【条件】如图,四边形ABCD中,AB=AD,90BADBCD【结论】452ACBACDBCCDAC①②----------------------------------------------------------------------------------------------------------------------【例8】如图,矩形ABCD中,AB=6,AD=5,G为CD中点,DE=DG,FG⊥BE于F,则DF为.【例9】如图,正方形ABCD的边长为3,延长CB至点M,使BM=1,连接AM,过点B作BNAM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为.【例10】如图,正方形ABCD的面积为64,BCE是等边三角形,F是CE的中点,AE、BF交于点G,则DG的长为.ONDCABM6HNMEFBCADFEDBAC【模型1】【条件】如图,四边形ABCD中,AB=AD,180BADBCDABCADC,12EAFBADEBCFCD,点在直线上,点在直线上【结论】BEDFEF、、满足截长补短关系【模型2】【条件】在正方形ABCD中,已知E、F分别是边BC、CD上的点,且满足∠EAF=45°,AE、AF分别与对角线BD交于点M、N.【结论】(1)BE+DF=EF;(2)S△ABE+S△ADF=S△AEF;(3)AH=AB;(4)C△ECF=2AB;(5)BM2+DN2=MN2;(6)△ANM∽△DNF∽△BEM∽△AEF∽△BNA∽△DAM;(由AO:AH=AO:AB=1:2可得到△ANM和△AEF的相似比为1:2);(7)S△AMN=S四边形MNFE;(8)△AOM∽△ADF,△AON∽△ABE;(9)△AEN为等腰直角三角形,∠AEN=45°;△AFM为等腰直角三角形,∠AFM=45°.(1.∠EAF=45°;2.AE:AN=1:2);(10)A、M、F、D四点共圆,A、B、E、N四点共圆,M、N、F、C、E五点共圆.半角模型7FEBCDAFEBCDAHGFCBDAE【模型2变型】【条件】在正方形ABCD中,已知E、F分别是边CB、DC延长线上的点,且满足∠EAF=45°【结论】BE+EF=DF【模型2变型】【条件】在正方形ABCD中,已知E、F分别是边C...