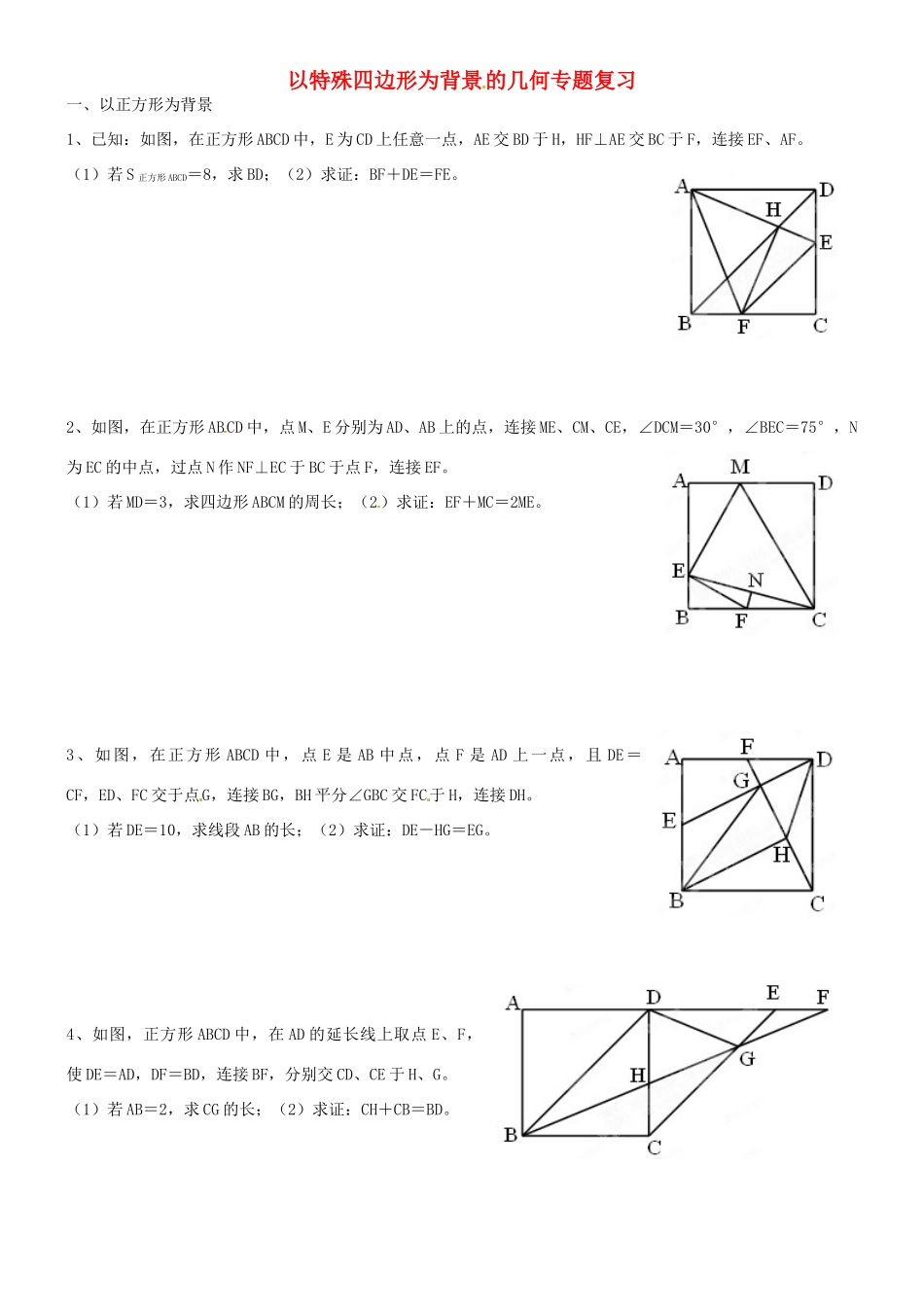
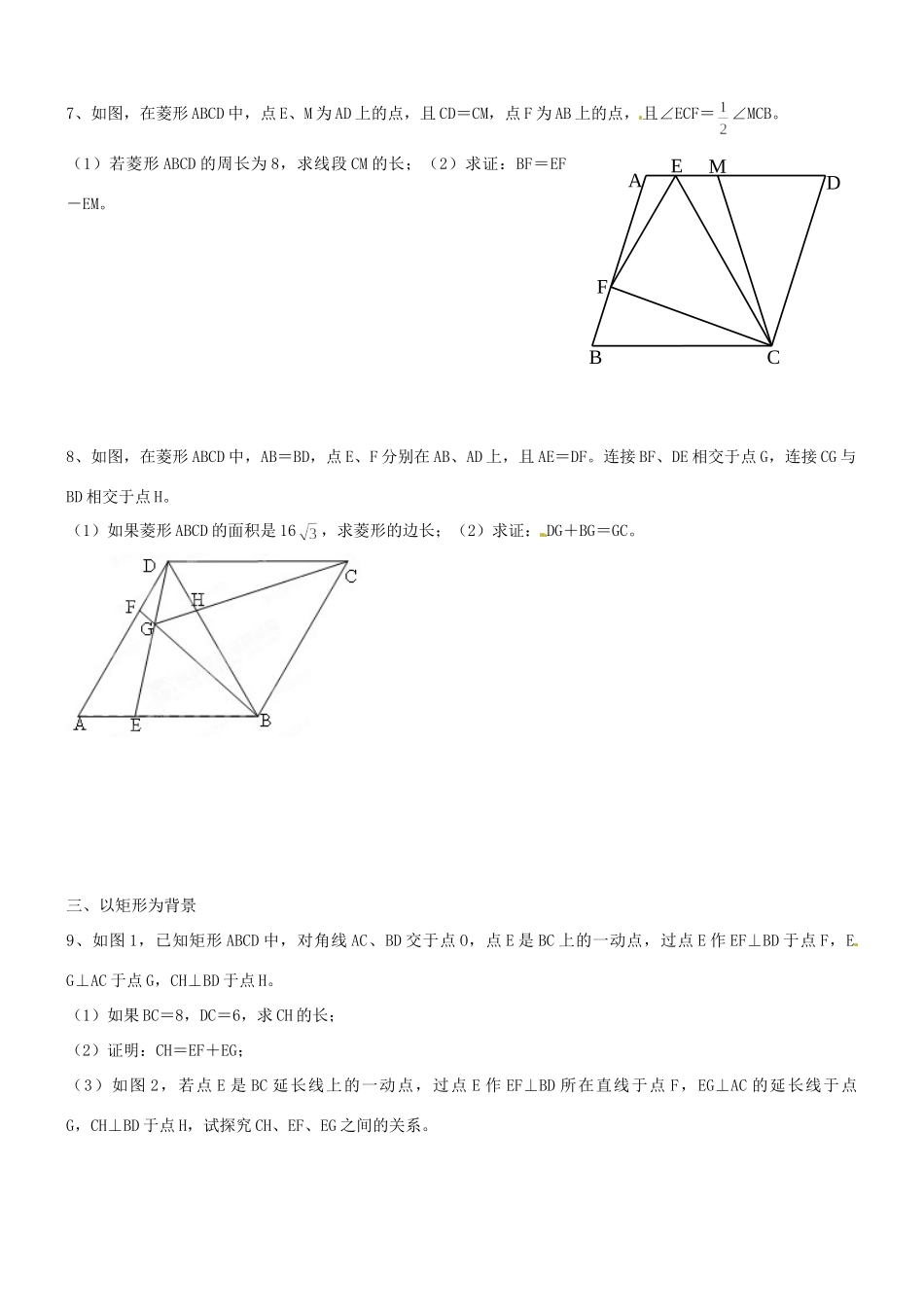
以特殊四边形为背景的几何专题复习一、以正方形为背景1、已知:如图,在正方形ABCD中,E为CD上任意一点,AE交BD于H,HF⊥AE交BC于F,连接EF、AF。(1)若S正方形ABCD=8,求BD;(2)求证:BF+DE=FE。2、如图,在正方形ABCD中,点M、E分别为AD、AB上的点,连接ME、CM、CE,∠DCM=30°,∠BEC=75°,N为EC的中点,过点N作NF⊥EC于BC于点F,连接EF。(1)若MD=3,求四边形ABCM的周长;(2)求证:EF+MC=2ME。3、如图,在正方形ABCD中,点E是AB中点,点F是AD上一点,且DE=CF,ED、FC交于点G,连接BG,BH平分∠GBC交FC于H,连接DH。(1)若DE=10,求线段AB的长;(2)求证:DE-HG=EG。4、如图,正方形ABCD中,在AD的延长线上取点E、F,使DE=AD,DF=BD,连接BF,分别交CD、CE于H、G。(1)若AB=2,求CG的长;(2)求证:CH+CB=BD。5、在正方形ABCD中,将∠ADC绕点D顺时针旋转一定角度,使角的一边与BC的交点为F,另一边与BA的延长线将于点E,连接EF,与BD将于点M。(1)若DE=,求EF的长;(2)若∠BEF的角平分线交BD于点G,求证:DF+BG=BD。二、以菱形为背景6、如图1,菱形ABCD中,点E、F分别为AB、AD的中点,连接CE、CF。(1)若∠B=60°,对角线BD=8,求对角线AC的长;(2)如图2,若H为AB上一点,连接CH,使∠CHB=2∠ECB,求证:CH=AH+AB。7、如图,在菱形ABCD中,点E、M为AD上的点,且CD=CM,点F为AB上的点,且∠ECF=∠MCB。(1)若菱形ABCD的周长为8,求线段CM的长;(2)求证:BF=EF-EM。8、如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF。连接BF、DE相交于点G,连接CG与BD相交于点H。(1)如果菱形ABCD的面积是16,求菱形的边长;(2)求证:DG+BG=GC。三、以矩形为背景9、如图1,已知矩形ABCD中,对角线AC、BD交于点O,点E是BC上的一动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H。(1)如果BC=8,DC=6,求CH的长;(2)证明:CH=EF+EG;(3)如图2,若点E是BC延长线上的一动点,过点E作EF⊥BD所在直线于点F,EG⊥AC的延长线于点G,CH⊥BD于点H,试探究CH、EF、EG之间的关系。MFEDCBA10、如图,矩形ABCD中,E为CB延长线上一点,且CE=CD,连接DE交AB于M,O是ED的中点,F是CD延长线上一点,连接RO交AD于G,过O作HK⊥OF,分别交DA的延长线于H,交DC于K。(1)若AD=3,DC=4,求梯形MBCD的面积;(2)求证:DF-DE=OD。11、如图,矩形ABCD中,E为AB上一点,AE=AD,F为BC延长线上一点,BF=AB,连接FE,过A作AG⊥FE交FE延长线于G,连接BG,且BG∥FD。(1)若AD=3,DC=5,求FD的长度;(2)求证:FE=2BG。