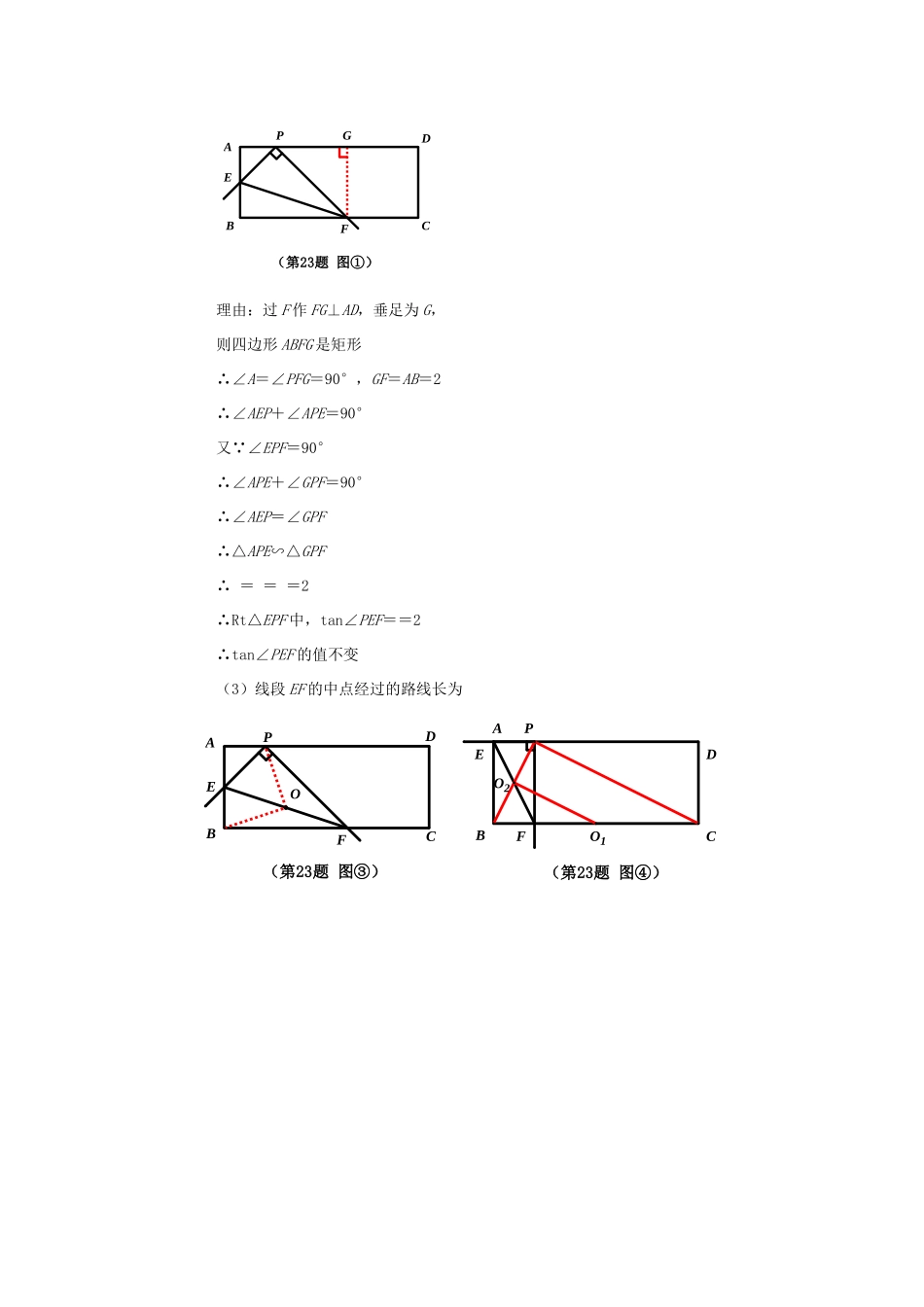
2011年各地中考数学压轴题精选11-20解析版2011福建三明22.解: 抛物线y=ax2-4ax+c过A(0,-1),B(5,0)∴解得:(2) 直线AB经过A(0,-1),B(5,0)∴直线AB的解析式为y=x-1由(1)知抛物线的解析式为:y=x2-x-1 点P的横坐标为m,点P在抛物线上,点Q在直线AB上,PQ⊥x轴∴P(m,m2-m-1),Q(m,m-1)∴S=PQ=(m-1)-(m2-m-1)即S=-m2+m(0<m<5)(3)抛物线的对称轴l为:x=2以PQ为直径的圆与抛物线的对称轴l的位置关系有:相离、相切、相交三种关系相离时:0<m<或<m<5;相切时:m=m=;相交时:<m<2011福建三明23.解:(1)在矩形ABCD中,∠A=∠D=90°,AP=1,CD=AB=2,则PB=.∴∠ABP+∠APB=90°又 ∠BPC=90°∴∠APB+∠DPC=90°∴∠ABP=∠DPC∴△APB∽△DCP∴=即=∴PC=2(2)tan∠PEF的值不变(第23题图①)GFPCDBAE理由:过F作FG⊥AD,垂足为G,则四边形ABFG是矩形∴∠A=∠PFG=90°,GF=AB=2∴∠AEP+∠APE=90°又 ∠EPF=90°∴∠APE+∠GPF=90°∴∠AEP=∠GPF∴△APE∽△GPF∴===2∴Rt△EPF中,tan∠PEF==2∴tan∠PEF的值不变(3)线段EF的中点经过的路线长为(第23题图④)(第23题图③)OO2O1FPCDFPCDBABAEE2011福建宁德25.(满分13分)解:⑴小颖摆出如图1所示的“整数三角形”:…………3分小辉摆出如图2所示三个不同的等腰“整数三角形”:…………8分⑵①不能摆出等边“整数三角形”.理由如下:设等边三角形的边长为a,则等边三角形面积为.因为,若边长a为整数,那么面积一定非整数.所以不存在等边“整数三角形”.…………10分;②能摆出如图3所示一个非特殊“整数三角形”:…………13分2011福建宁德26.(满分13分)解:⑴①直线与坐标轴交点坐标是A(6,0),B(0,-6);…………1分②如图1,四边形DCEF即为四边形ABEF沿EF折叠后的图形;…………3分⑵ 四边形DCEF与四边形ABEF关于直线EF对称,又AB∥EF,∴CD∥EF. OA=OB,∠AOB=90°,∴∠BAO=45°. AB∥EF,∴∠AFE=135°.∴∠DFE=∠AFE=135°.861012513图143355554438101066图245121513图3ABEFHOxyDCG图11234567-3-2-14321-1-3-5∴∠AFD=360°-2×135°=90°,即DF⊥x轴.∴DF∥EH,∴四边形DHEF为平行四边形.…………5分要使□DHEF为菱形,只需EF=DF, AB∥EF,∠FAB=∠EBA,∴FA=EB.∴DF=FA=EB=t.又 OE=OF=6-t,∴EF=.∴=t.∴.∴当时,□DHEF为菱形.…………7分⑶分两种情况讨论:①当0<t≤3时,…………8分四边形DCEF落在第一象限内的图形是△DFG,∴S=. S=,在t>0时,S随t增大而增大,∴t=3时,S最大=;…………9分②当3<t<6时,…………10分四边形DCEF落在第一象限内的图形是四边形DHOF,∴S四边形DHOF=S△DGF—S△HGO.∴S===.ABEFHOxyDCG图21234567-3-2-1431-1-3-5 a=<0,∴S有最大值.∴当t=4时,S最大=6.…………12分综上所述,当S=4时,S最大值为6.…………13分2011福建南平25、(2011•南平)(1)操作发现:如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.(2)类比探究:如图2,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.考点:翻折变换(折叠问题);全等三角形的判定与性质;角平分线的性质;平行四边形的性质;矩形的性质。分析:(1)根据翻折的性质得出BE=EF,∠B=∠EFA,利用三角形全等的判定得△ECG≌△EFG,即可得出答案;(2)利用平行四边形的性质,首先得出∠C=180°﹣∠D,∠EFG=180°﹣∠AEF=180°﹣∠B=180°﹣∠D,进而得出∠ECG=∠EFG,再利用EF=EC,得出∠EFC=∠ECF,即可得出答案.解答:(1)猜想线段GF=GC,证明: E是BC的中点,∴BE=CE, 将△ABE沿AE折叠后得到△AFE,∴BE=EF,∴EF=EC, EG=EG,∠C=∠EFG=90°,∴△ECG≌△EFG,∴FG=CG;(2)(1)中的结论仍然成立.证明: E是BC的中点,∴BE=CE, 将△ABE沿AE折叠后得到△AFE,∴BE=EF,∠B=∠AEF,∴EF=EC,∴∠EFC=∠ECF, 矩形ABCD改...